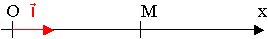1eS - Chap 03 - Mouvements

I ) Mouvement d'un point :

1) Relativité du mouvement:

Définition : On appelle référentiel un objet par rapport auquel le physicien étudie le mouvement. Tout mouvement est relatif au référentiel utilisé.

2) Repère d'espace:

Pour définir la position d'un mobile, il est nécessaire d'associer un repère au référentiel, système d’axes à 1, 2 ou 3 dimensions.

repère à une dimension

pour un mouvement rectiligne

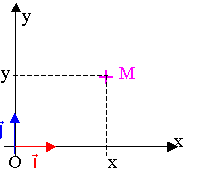
repère à 2 dimensions

pour un mouvement plan

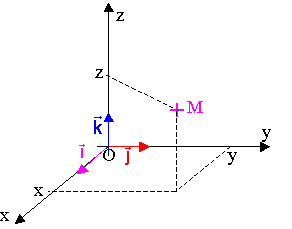
repère à 3 dimensions

pour un mouvement dans l’espace

3) Instant t :

Un mouvement se définit aussi dans le temps. La position du mobile dépend de l’instant t.

II) Vitesse :

1) Vitesse moyenne:

Définition : La vitesse moyenne Vm d'un solide est le rapport de la distance d parcourue par le temps mis pour la parcourir.

Elle s'exprime en m.s^-1 ou en km.h^-1

Vm = d / t avec d en mètre (m) ; t en seconde (s) et Vm en m.s^-1

2) Vitesse instantanée :

Définition : La vitesse instantanée d'un solide à un instant t se définit comme la vitesse moyenne du solide pendant une brève durée autour de la date t.

Remarques :

➢ La vitesse du mobile dépend du référentiel utilisé.

➢ La vitesse instantanée se mesure avec un compteur de vitesse d'un véhicule ou d’un radar.

➢ Le mouvement est uniforme si la vitesse instantanée reste constante.

➢ Le mouvement est accéléré si la vitesse instantanée augmente dans le temps.

➢ Le mouvement est décéléré si la vitesse instantanée diminue dans le temps.

3) Vecteur vitesse :

Définition : A un instant de date t, le mouvement d'un mobile est déterminé par :

➢ La position du mobile.

➢ Le vecteur vitesse du mobile caractérisé par :

* sa direction : la tangente à la trajectoire.

* son sens : celui du mouvement.

* sa valeur : la vitesse instantanée du mobile.

Activité : Tracé de vecteurs vitesse sur des enregistrements réalisés sur table à mobiles autoporteurs.

III) Mouvement d'un solide indéformable

1) Définition :

Un solide indéformable correspond à un objet dont la distance entre deux points quelconques ne varie pas au cours du temps.

2) Trajectoires :

Définition: La trajectoire d'un mobile est l'ensemble des positions successives de ce mobile au cours du temps.

➢ Le mouvement d'un objet est curviligne si sa trajectoire est une courbe.

➢ Le mouvement d'un objet est rectiligne si sa trajectoire est une droite.

➢ Le mouvement d'un objet est circulaire si sa trajectoire est un cercle.

3) Mouvement de translation:

Définition: Un solide est en mouvement de translation si tout segment du solide reste parallèle à lui même au cours du mouvement.

Translation rectiligne: Tout segment du solide se déplace en restant parallèle à lui même et le mouvement de chaque point est rectiligne.

Une voiture roulant en ligne droite est en translation rectiligne.

Translation curviligne: Tout segment du solide se déplace en restant parallèle à lui même et le mouvement de chaque point est curviligne.

Une cabine d’un téléphérique est en translation curviligne

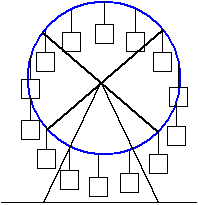
Translation circulaire: Tout segment du solide se déplace en restant parallèle à lui même et le mouvement de chaque point est un cercle.

Une cabine d’une grande roue de foire est en translation circulaire.

4) Solide en rotation autour d'un axe fixe:

Définition : Un solide est en mouvement de rotation autour d'un axe fixe si le mouvement de chacun de ses points est un cercle centré sur l'axe de rotation.

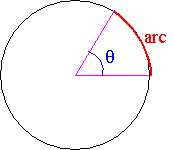
Définition: La vitesse angulaire moyenne est le rapport de l'angle de rotation θ du solide par le temps t mis pour effectuer cette rotation.

ω_m = θ / t avec ω_m en rad.s^-1 ; θ en radians (rad) et t en seconde (s)

exercice : calculer la vitesse angulaire d’une trotteuse de montre

La trotteuse fait un tour en une minute. θ = 2 π pour t = 60s . ω_m = 2 π / 60 = 0,105 rad.s^-1

Définition: La vitesse angulaire instantanée d'un solide à la date t se définit comme la vitesse angulaire moyenne du solide pendant une brève durée autour de la date t.

ω = ( θ₂ - θ₁ ) / ( t₂ – t₁) avec ω en rad.s^-1 ; θ en radians (rad) et t en seconde (s)

Relation entre vitesse instantanée et vitesse angulaire :

Activité sur feuille (matériel fil , rapporteur, règle) Relation entre longueur de l’arc et angle

Tracer différents cercles de 2, 7, 10 et 12 cm de rayon

Mesurer avec un fil la longueur de l’arc pour un angle et un rayon donné.

Angle α en degré	45	90	135	180	90	90	90
Rayon R en cm	10	10	10	10	2	7	12
arc d en cm	7,8	15,7	23,6	31,4	3,14	11	18,8
α en radian	0,785	1,57	2,36	3,14	1,57	1,57	1,57
R . α (α en rad)	7,85	15,7	23,6	31,4	3,14	11	18,8

Conclusion : La longueur d d’un arc de cercle de rayon R et d’angle α :

d = R . α avec α en radian (rad) , d et R sont en cm ou en m

ω = α / t v = d / t v = R . α / t ➔ v = R . ω

v = R . ω

avec v : vitesse en m.s^-1 ; R : rayon de la trajectoire en m et ω : vitesse angulaire en rad.s^-1

Si la vitesse angulaire d’un point d’un solide en rotation est constante au cours du temps, celle de tout le solide l’est aussi. La rotation est à vitesse constante.

5) Centre d'inertie

Définition: Le centre d'inertie d'un solide en mouvement est le point de ce solide dont le mouvement est le plus simple. On le note G.

C’est le barycentre de tous les points matériels du solide affectés de leur masse.

G coïncide avec le centre de gravité défini en 3^ème . C’est le centre de répartition des masses.

Le centre d’inertie d’un solide homogène est son centre géométrique.

exemple : on lance un marteau vers le haut. Il tourne sur lui-même, tout en se déplaçant.

Son centre d’inertie G décrit une parabole.