Chap 12 – Lumière et mesures de distances

I ) Propriétés de la lumière :

1) Propagation de la lumière :


Si on envoie un rayon lumineux issu d'un laser vers une série de trous alignés, on constate que la lumière passe bien par tous les trous.

Dans le vide et dans l’air, la lumière se propage en ligne droite. Sa trajectoire est rectiligne.

Avec un laser et de la poussière de craie, on peut observer le faisceau lumineux rectiligne.

On modélise sur un schéma optique le trajet de la lumière par une ligne droite fléchée dans le sens de propagation, que l’on appelle rayon lumineux.

 

2) Vitesse de la lumière :

Lorsqu'on allume la lumière dans une pièce, elle est immédiatement présente partout.

A notre échelle, on peut considérer la vitesse de lumière comme infinie et son déplacement comme instantané.

Mais à une grande échelle comme dans l’espace, cette vitesse est bien de valeur finie.

Elle a été mesurée en 1676 par un astronome Danois, M. Römer.

Elle se note c et s’appelle parfois célérité.

Dans le vide,    c  = 299 792 458 m.s-1 » 300 000 km.s-1 ou 3,00.108 m.s-1

Elle varie lorsqu'elle change de milieu.

 

3) L’année-lumière :

En astronomie, les distances sont énormes, on utilise donc des unités adaptées comme l’année-lumière ( a.l. ) .

L’année-lumière est la distance parcourue par la lumière en une année.

         1 a.l. = c . t = 3.108 x 365,25 x 24 x 3600 = 9,46 . 1015 m

         1 a.l. » 1016 m  ou 1013 km

Une distance de 10 a.l. correspond à 10 ans de propagation de la lumière dans le vide.

Remarque : on voit des étoiles dans le ciel, très éloignées, plus elles le sont et plus ce que l’on voit est ancien, cette lumière a été émise il y a longtemps et a mis du temps pour nous parvenir.

« Voir loin, c’est voir dans le passé. »

II ) Applications à la mesure de distance :

1) La visée :


Voir TP détermination de distance

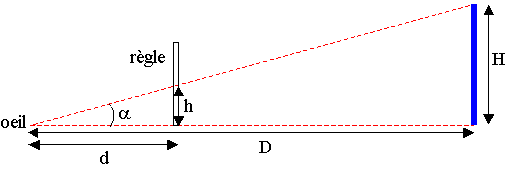
On cherche à déterminer la hauteur H d'une montagne dont on connaît la distance D.

On utilise une règle graduée que l'on place verticalement à une petite distance d de son œil.

On vise le bas de la montagne que l'on aligne avec le zéro de la règle, puis on lit à quelle graduation correspond le haut de la montagne sans bouger.

Pour déterminer la valeur de H, on utilise le théorème de Thalès du triangle rectangle :

H / h = D / d    Þ  H = h . D / d

Exemple : La montagne se situe à 5 km.

En plaçant la règle à 50 cm, on lit une hauteur h de 27 cm.

H = 27.10-2 x 5000 / 50.10-2 = 2700 m

Si l'expérience a été réalisée à Passy, à 600 m d'altitude, le sommet de la montagne est à 3300 m.

On vérifie ensuite sur une carte si l'altitude correspond au calcul précédent.

 

2) Mesure de distance en utilisant l’écho :

On peut utiliser le phénomène d'écho de la lumière pour déterminer une distance.

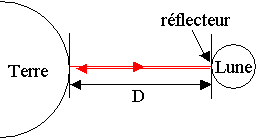En 1969, les astronautes de la mission Apollo ont placé sur le sol lunaire un réflecteur permettant de réfléchir la lumière d'un puissant laser émettant depuis la Terre.

En mesurant la durée Dt du trajet aller-retour de la lumière entre la Terre et la Lune, on peut calculer la distance D Terre-Lune.

Attention, il faut bien tenir compte de la distance totale parcourue, soit 2 fois la distance mesurée

 

c = 2D / Dt    Þ  D = c. Dt / 2 = 3,00.108 x 2,56 / 2 = 3,84.108 m = 384 000 km

Le sonar d'un bateau utilise aussi la technique d'écho appliquée aux ultrasons dans l'eau. C'est un émetteur-récepteur qui permet de mesurer la profondeur des fonds marins et de détecter des bancs de poissons.

Etudier l’exercice Résolu p 193

 

©Sciences Mont Blanc