Correction Bac Réunion Juin 2002

 

I ) Qualité d'un capteur de tension ( 5,5 points)

II ) Le jongleur à cheval (5,5 points)

III ) A propos de Michel Eugène Chevreul, chimiste français (4 points)

IV ) Etude d'un comprimé de la vitamine C (5 points)

 

 

Correction Bac Réunion Juin 2002 - I ) Qualité d'un capteur de tension :

I ) Préliminaires :

du_C/dt + u_C / RC = 0  Þ  RC = - u_C / (du_C/dt)  
Þ  [RC] = U / (U / T) = T
RC est donc bien homogène à une durée.  t = R.C

 

 

II ) Etude expérimentale à l'oscilloscope à mémoire :

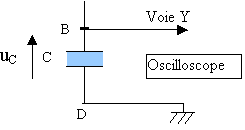
1)     a) L'entrée Y de l'oscilloscope est reliée au point B et la masse M au point D.
b) Si le condensateur est bien déchargé, pour étudier la charge, il faut basculer l'interrupteur K sur la position 1.

2)     a) Sur l'oscillogramme de la figure 3, u_{C max} = E = k_V . N_V  = 2 x 1 = 2 V.
Sur l'oscillogramme de la figure 4, N_V = 4 div pour une même valeur E,
k_V = E / N_V = 2 / 4 = 0,5 V.div^-1  ( sensibilité verticale )
b) La base de temps a été diminuée car le début de la courbe a été agrandi.

3)     a) D'après la courbe, t' = k_S.N_S = 10 x 1 = 10 ms
b) t' = t. Cette durée est identique pour la charge et la décharge.
c) t' = t = R.C Þ R = t' / C = 10.10^-3/ 1,0.10^-6 = 1,0.10⁴ W

4) La durée t' est identique pour la charge et la décharge.
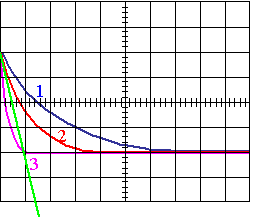
Dans le cas de la décharge, la tangente à l'origine coupe l'asymptote horizontale ( u = 0 V ).
Seule la courbe 2 correspond à t = 10 ms.

 

 

 

 

 

III ) Etude expérimentale suivie par informatique

1)     Le phénomène non étudié se situe entre les dates t₁ et t₂.

 

2)     a) Si le capteur de tension se comportait comme une bobine de résistance négligeable, la tension u_C subirait des oscillations.

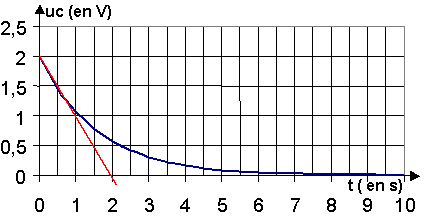
b) On trace la tangente à l'origine, qui coupe l'asymptote (u=0V) au temps t.    t = 2 s.     t = R_V.C 
R_V= t / C = 2 / 1,0.10^-6= 2,0.10⁶ W

 

 

 

IV ) Conclusion sur la qualité du capteur

1) Les 2 résistances sont en dérivation :  u_R = u_V

2) R.i_R = R_V.i_V  Þ  i_V / i_R = R / R_V = 1,0.10⁴ / 1,0.10⁶ = 0,01.  i_V est donc négligeable devant i_R.

3) Il faut que R_V soit très grande par rapport à R pour que le capteur de tension ne perturbe pas les mesures.

 

©Sciences Mont Blanc

 

 

 

 

Correction Bac Réunion Juin 2002 - II ) Le jongleur à cheval :

1) a) Un repère galiléen est un repère dans lequel on peut appliquer le principe d'inertie. Toutes les lois de Newton y sont applicables.

 

b) Le point C se déplace parallèlement à l'axe horizontal et le vecteur v_H du point C est constant.

Le point C a donc un mouvement horizontal rectiligne et uniforme.

 

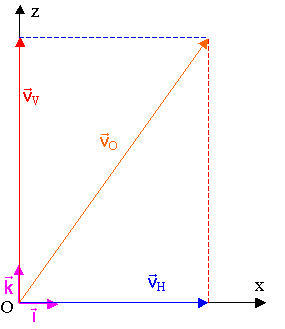
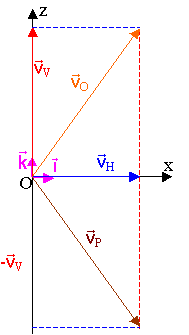
2) Tracé des vecteurs

 

3) a) Les forces de frottement étant négligées, la seule force exercée sur la balle après le lancement est le poids de la balle. La balle est en chute libre.

 

b) On applique la relation fondamentale de la dynamique (deuxième loi de Newton) au point B dans le référentiel terrestre supposé galiléen :

m . a= P       Þ  m . a = m .g          Þ   a = g   

On projète sur l'axe Oz   :     a_Z = g_Z   Þ  dv_Z/dt = - g  Þ  v_Z = - g.t + v_{Z 0} = - g.t + v_V

On projète sur l'axe Ox   :     a_X = g_X   Þ  dv_X/dt = 0  Þ  v_X = v_{X 0} = v_H

v_Z = dz/dt = - g.t + v_V   Þ  z(t) = - ½ g.t² + v_V.t + z₀ = - ½ g.t² + v_V.t      ( z₀ = 0 )

v_X = dx/dt = v_H   Þ  x(t) = v_H.t + x₀ = v_H.t      ( x₀ = 0 )

 

c) x_B = v_H.t  Þ t = x_B / v_H  .  On remplace t par cette expression dans l'équation horaire de z_B

z_B = - ½ g.t² + v_V.t = - ½ g.( x_B / v_H )² + v_V.( x_B / v_H ) 

z_B = - (g / 2 v_H²).x_B² + (v_V/v_H).x_B

 

4) Au point P , z_P = 0 car on est sur l'axe Ox.

z_P = 0 = - ½ g.t_P² + v_V.t_P = t_P . ( - ½ g.t_P + v_V)   Þ  - ½ g.t_P + v_V = 0 

Þ  t_P = 2 v_V / g = 2 x 7,0 / 9,8 = 1,4 s

x_P = v_H . t_P = 2 v_V . v_H / g = 2 x 7,0 x 5,0 / 9,8 = 7,1 m 

 

5) a) Le point A a un mouvement horizontal, rectiligne et uniforme de vitesse constante v_H.

z_A(t) = constante = 0  et  x_A(t) = v_H . t

 

b) Pour récupérer la balle, il faut que z_B soit nulle, ce qui correspond au point P.

Au point P,  x_A = v_H . t_P = x_P     ( en fait, quelquesoit t, x_A = x_P = v_H. t )

Le jongleur récupére donc toujours la balle à condition que le cheval garde bien une vitesse constante, car si ce n'est pas le cas, l'expression de x_A change alors que celle de x_P ne change pas car elle ne dépend que de la vitesse initiale du cheval.

En pratique, ce n'est pas facile.

6) a) D'après le tracé de vecteur,  v_O² = v_V² + v_H²   ,  v_O = ( v_V² + v_H² )

Au sommet de sa trajectoire, z_B est maximum, v_Z = dz_B/dt = 0.

v_X = v_H   ;   v_S = ( v_X² + v_Z² ) = v_H

b) Théorème de l'énergie cinétique appliqué à la balle dans un référentiel galiléen entre O et S :

Ec_S - Ec_O = W(P)   ;   ½ m ( v_S² – v_O² ) = m . g . ( z_O - z_S ) = - m . g . h  

h = ( v_O² – v_S² ) / 2g = ( ( v_V² + v_H² ) - v_H² ) / 2g = v_V² / 2g

 

Théorème de l'énergie cinétique appliqué à la balle dans un référentiel galiléen entre O et P :

Ec_P - Ec_O = W(P)    ;   ½ m ( v_P² – v_O² ) = m . g . ( z_O - z_P ) = 0  

  v_P = v_O = ( v_V² + v_H² )

 

Au point P,  t_P = 2 v_V / g    ,   v_X = v_H   , 

v_Z = - g.t_P + v_V = - g .(2 v_V/g) + v_V = - v_V.

 

Les vecteurs v_O et v_P ont même intensité et sont symétriques par rapport à l'axe Ox.

 

 

©Sciences Mont Blanc

 

 

Correction Bac Réunion Juin 2002 - III ) A propos de Michel Eugène Chevreul chimiste français :

 

©Sciences Mont Blanc

 

 

Correction Bac Réunion Juin 2002 -IV ) Etude d'un comprimé de la vitamine C:

I ) Dosage :

Elle décide de procéder à un dosage par une solution de soude (ou hydroxyde de sodium) pour vérifier l'indication de masse de l'acide ascorbique. Elle prépare tout d'abord un volume 

V₀=200,0 mL de solution aqueuse avec la totalité du comprimé. Soit S la solution obtenue.

1)a)   HA_(aq) + HO^-_(aq) = A^-_(aq) + H₂O_(l)

b) K_r = [A^-]_éq /([HA]_éq.[HO^-]_éq) = ([A^-]_éq .[H₃O⁺]_éq/[HA]_éq) /([H₃O⁺]_éq.[HO^-]_éq ) = Ka / Ke

K_r = 10^-4,1 / 10^-14 = 10^9,9 = 7,9.10⁹

c) K_r > 10⁴. On peut considérer la réaction comme totale. En supposant qu'elle est rapide et unique, on peut l'utiliser comme réaction de dosage.

d) A l'équivalence, les quantités de matière d'acide et de base mises en présence sont dans les proportions stoéchiométriques.

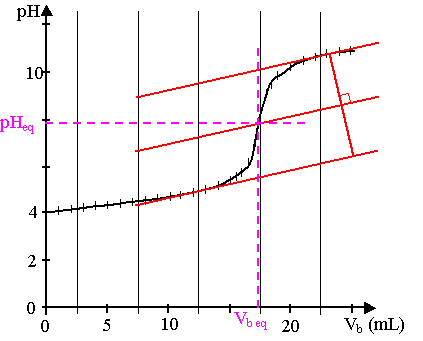
2) On utilise la méthode des tangentes et on en déduit V_{b eq} = 17,2 mL et pH_éq = 7,9.

A l'équivalence, on a :  n(HA)₀ =n(HO^- )_éq  Þ C.V = C_b.V_{b eq} 

C = C_b.V_{b eq}/V = 2,00.10^-2x17,2.10^-3/50.10^-3 C = 6,9.10^-3 mol.L^-1

m = n.M = C.V₀.M

m = 6,9.10^-3 x 200,0.10^-3 x 176 = 0,24 g

 

 

 

 

 

 

 

II ) Interprétation :

1) n(HA) = m / M = 247,7.10^-3 / 176 = 1,41.10^-3 mol

n(A^-) = m'/ M' = 284.10^-3 / 198 = 1,43.10^-3 mol

2) a) HA_(aq) + H₂O_(l) = A^-_(aq) + H₃O⁺_(aq)       Ka = [A^-]_éq.[H₃O⁺]_éq / [HA]_éq

- logKa = -log [H₃O⁺] – log([A^-]_éq / [HA]_éq)  Þ  pKa = pH – log([A^-]_éq / [HA]_éq) 

pH = pKa + log([A^-]_éq / [HA]_éq) 

On admet qu'à l'équilibre, [A^-]_éq = [HA]_éq .   On a donc pH = pKa = 4,1

La valeur expérimentale donnée par la courbe au départ est voisine de 4.

b) Une solution d'un couple acide base faible où les quantités d'acide et de base conjuguée sont égales est une solution tampon.

Un ajout modéré d'acide ou de base forte dans une telle solution modifie très peu le pH.

La dilution d'une telle solution modifie très peu le pH.

3)a) A un pH de 1 inférieur au pKa du couple, la forme acide HA prédomine.

b) Au pH de l'estomac, on peut considérer que la base conjuguée A^- est négligeable devant HA.  n(HA)_estomac = n(HA)₀ + n(A^-)₀ = 1,41.10^-3 + 1,43.10^-3 = 2,84.10^-3 mol

m(HA) = n.M = 2,84.10^-3 x 176 = 0,500 g = 500 mg

Cela correspond donc à l'indication "acide ascorbique total : 500 mg" portée par la notice.

 

©Sciences Mont Blanc