Correction Bac France - Juin 2003

Calculatrice non autorisée

 

I ) Etude de la vitamine C (4 points)

I ) Etude d'un médicament (4 points) (spe)

II ) Charge d'un condensateur à l'aide d'une pile (7 points)

III ) Autour du radium (4 points)

 

 

Correction France - Juin 2003 - I ) Etude de la vitamine C

I ) Etude de la réaction entre une solution aqueuse d'acide ascorbique et une solution aqueuse d'hydroxyde de sodium :

acide ascorbique : HA , C_A=1,00 10^-2 mol.L^-1 et soude C_B=2,00 10^-2mol.L^-1 ; V_A = 20,0 mL et 

1) équation : HA_(aq) + HO^-_(aq) = A^-_(aq) + H₂O_(l)
2) V_B = 5,0 mL a)  pH = 4,0.  [H₃O⁺]_éq = 10^-pH = 10^-4,0 mol.L^-1 

b) [HO^-]_éq = Ke / [H₃O⁺]_éq = 10^{-14 + 4,0} = 10^-10 mol.L^-1
 n_f(HO^-) = [HO^-]_éq x V = 10^-10 x 25.10^-3= 2,5.10^-12 mol

c)

Equation de la réaction		HA(aq)          +     HO- (aq)   =  A-(aq)      +   H2O(l)
Etat du système	Avancement	Quantité de matière en mol
Etat initial	0	n0(HA)=CA.VA	CB.VB	0	0
Etat final	xf	nf(HA)= CA.VA -xf	CB.VB -xf	xf	xf

C_A.V_A = 1,00.10^-2 x 20,0.10^-3 = 2,00.10^-4 mol   ;  C_B.V_B = 2,00.10^-2 x 5,0.10^-3 = 1,0.10^-4 mol  

n_f(HO^-) = C_B.V_B -x_f = 2,5.10^-12 mol ;  x_f » 1,0.10^-4 mol

d) Si la réaction est totale , C_B.V_B -x_max = 0 ( HO^- est en défaut ) ; x_max = C_B.V_B = 1,0.10^-4 mol

t = x_f / x_max = 1. La réaction est totale. Cette réaction est rapide, totale et unique, elle peut donc servir de support pour doser une solution aqueuse d'acide ascorbique par une solution de soude.

II ) Dosage colorimétrique d'un comprimé de vitamine C :

Un comprimé de "vitamine C 500" dans une fiole jaugée de 100,0 mL avec l'eau distillée  ( S ).  V_A=10,0mL de  S dosé avec une solution de soude C_B=2,00.10^-2 mol.L^-1.V_BE=14,4mL
1) schéma annoté du  titrage.

2) D'après la courbe de titrage sur la figure de l'annexe,
pH_E vaut près de 8, l'indicateur coloré le mieux adapté est donc le rouge de crésol dont la zone de virage comprend pH_E 

3) A l'équivalence, les réactifs ont été ajoutés dans les proportions stœchiométriques. n(HA)₀ = n(HO^- )_{versé à l'équivalence}

4) n(HA)₀ = C_B.V_BE = 2,00.10^-2 x 14,4.10^-3 = 2,88.10^-4 mol

5) La quantité n(HA)₀ correspond à V_A=10,0 mL de solution S
Dans la fiole de 100,0 mL, il y a 10 fois plus de HA. n(HA)_comprimé = 10 n(HA)₀ = 2,88.10^-3 mol

M(C₆H₈O₆) = 6 x 12,0 + 8 x 1,0 + 6 x 16,0 = 176 g.mol^-1  . 
m = n x M = 2,88.10^-3 x 176 = 0,507 g = 507 mg

L'indication du fabricant "vitamine C 500" correspond en fait à la masse d'acide ascorbique dans un comprimé. la différence est due aux erreurs d'expérience ou de fabrication.

Annexe: à rendre avec la copie

 

III ) Etude de la molécule d'acide ascorbique :

Le groupe fonctionnel (1) correspond à la famille des esters.

Le groupe fonctionnel (2) correspond à la famille des alcools

 

 

 

 

 

 

©Sciences Mont Blanc

 

 

 

Correction France - Juin 2003 - I ) Etude d'un médicament (spe)

 

1) Fe³⁺_(aq) + e^-  = Fe²⁺_(aq) 

2.1) Il faut une burette de 25,0 mL pour prélever S, une pipette jaugée de 2,00 mL pour la solution d'o-phénanthroline, une pipette jaugée de 1,00 mL pour la solution d'hydroquinone, une fiole jaugée de 50,0 mL

2.2) Dilution : m_avant = m_après ;  t₁.V₁ = t .V ;  t_l = t .V/ V₁ = 20,0 x 25,0/50,0 = 10,0 mg.L^-1  

2.3) Il faut que tous les ions Fe²⁺  réagissent avec l'o-phénanthroline pour chercher la relation entre l'absorbance A et la concentration en ions fer (II).

2.4) Le coefficient directeur est k = 1,80 / 10,0.10^-3  = 180 L.mg^-1  ;  A = 180 x t    avec t en g.L^-1

3.1) Le colorant est de couleur rose, couleur voisine de celle de la solution contenant des ions Fe²⁺_(aq) et l'o-phénanthroline. Ce colorant absorbe sans doute autour de 500nm et peut donc perturber les mesures.

3.2) t'₀ = A / 180 = 1,35 / 180 = 0,00750 g.L^-1 =7,50 mg.L^-1

t₀ = t'₀ .V'₀ / V₀ = 7,50 x 50,0/5,00 = 75,0 mg.L^-1

3.3) La masse du fer dans un comprimé est de 75 mg car on a dissous un comprimé dans 1L d'eau L'écart relatif est 80-75 / 80 = 6,25 %.

3.4) n(Fe²⁺) = 256,30.10^-3 / (55,8 + 32,1 + 4 * 16+ x.18 )= 256,30.10^-3 / (151,9 + 18 x)

n(Fe²⁺) = 80.10^-3 / 55,8   Þ 256,30.10^-3 * 55,8 / 80.10^-3 = 151,9 + 18 x ;   x = 1,49 » 1,5

 

 

©Sciences Mont Blanc

Correction France - Juin 2003 - II ) Charge d'un condensateur à l'aide d'une pile :

 

1 ) Réalisation d'une pile :

1.1)  Schéma
1.2)  Q_{r , i} = [Zn ²⁺]_i / [Cu²⁺]_i = C₁ / C₂ = 1,0 / 1,0 = 1

Q_{r ,i}  < K  Þ Le système évolue dans le sens direct de l'équation : Cu²⁺_(aq) + Zn_(s) = Cu_(s) + Zn ²⁺_(aq)

1.3)  A l'électrode de cuivre :  Cu²⁺_(aq) + 2 e^- = Cu_(s)

A l'électrode de zinc     :  Zn_(s) = Zn ²⁺ _(aq) + 2 e^-

1.4)  L'électrode de zinc donne des électrons au circuit, c'est donc le pôle - ; l'électrode de cuivre reçoit les électrons, c'est donc le pôle Å

1.5) D'après le sens de la réaction, les réactifs sont le métal zinc et les ions Cu²⁺ , le métal zinc est en excès, les ions Cu²⁺ sont donc en défaut.

n(Cu²⁺)₀ = C₂ x V₂ = 1,0 x 0,1 = 0,1 mol.  n(Cu²⁺)_f = n(Cu²⁺)₀ – x_f = 0 , x_f = n(Cu²⁺)₀ =0, 1 mol

D'après la demi-équation, n(e^- ) = 2 n(Cu²⁺)₀ = 0,2 mol.

Quantité max d'électricité : Q_max = n(e^-).F = n(e^-).N_A.e = 0,2 x 6,02.10²³ x 1,6.10^-19 = 1,93.10⁴ C

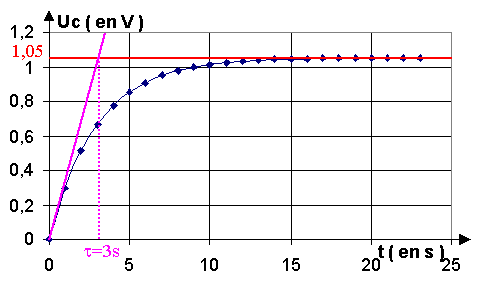
2.1 Lorsque le condensateur est chargé complètement, les électrons ne circulent plus , il n'y a plus

     de courant dans le circuit : i = 0 A.  La valeur de E correspond à la valeur de u_C lorsque le

     condensateur est chargé , lorsque l'intensité i est nulle:   E = 1,05 V

2.2.1.  t = r . C   où r est la résistance interne de la pile et C la capacité du condensateur.
           [t] = [r].[C]   ,  u_r = r.i  Þ [r] = U / I  ;  q = C.u_C = I.t  Þ [C] = I.T/ U
           [t] = ( U / I ).(I.T / U) = T   Þ t a bien la dimension d'un temps
2.2.2.  On trace la tangente à l'origine , elle coupe l'asymptote à la courbe au temps t.    t = 3 s
2.2.3.  r = t / C = 3 / 330.10^-6 = 9 090 W

2.3.1.  i = dq / dt
2.3.2.  q = C.u_C
2.3.3.  D'après le montage, la loi des tensions indique : u_PN = u_C Þ E – r.i = u_C  Þ E = u_C + r.i
           i = dq / dt = C.du_C / dt   Þ   E = u_C + r.C.du_C/dt  (1)
2.3.4.  u_C(t) = E.( 1 – e^{- a.t})   ;  du_C / dt = a.E.e ^{- a.t}   ;  (1) E = E.( 1 – e ^{- a.t} ) + r.C.a.E.e ^{- a.t}

           0 = ( r.C.a – 1 ).E.e ^-a.t   ; pour que ceci soit valable quelquesoit l'instant t, il faut que :
           r.C.a - 1 = 0  Þ a = 1 / (R.C)

 

ANNEXE – FIGURE 3

 

©Sciences Mont Blanc

 

 

 

Correction France - Juin 2003 - III ) Autour du radium

1. Affirmation fausse. 84 désigne Z le nombre de protons et 208 désigne A le nombre de nucléons.

    Il y a donc 84 protons et 124 neutrons.

2. Affirmation fausse. Il existe un défaut de masse Dm entre la masse des nucléons et celle du noyau :  Dm = m(nucléons) – m(noyau)

3. Affirmation exacte. La particule a est bien un noyau . L'équation vérifie bien les lois de conservation de Soddy, conservation du nombre de protons et du nombre de nucléons.

4. Affirmation fausse. Des isotopes ont le même nombre de protons Z et un nombre de neutrons différents. Or ici, Z est différent pour ces noyaux.

5. Affirmation fausse. L'équation de désintégration b^- est : ®+

6. Affirmation vraie.  t ½ = 3,8 jours  ;  t = 3 x t ½ = 11,4 jours

N = N₀.e ^{– ln2 . t / t ½}  ;  N / N₀ = 2 ^{-t / t ½}  = 1/ 2³ = 1 / 8 = 12,5 %

7. Affirmation fausse. Une désintégration a diminue le nombre de nucléons de 4 ; une désintégration b^- ne modifie pas le nombre de nucléons.

Pour passer de  à , il faut diminuer le nombre de nucléons de 12, ce qui correspond à 3 désintégrations a et non 2.

8. Affirmation fausse.  A = 6,0.10⁵ Bq .  1 bq = 1 désintégration par seconde.
A = 6,0.10⁵ x 60 = 3,6.10⁷ désintégrations par minute.

9. Affirmation fausse.      E = Dm.c² = [m() – (m( )+m())].c²
E = (3,752438.10^-25 - 6,64465.10^-27 - 3,685904.10^-25 ) x (2,998.10⁸)² = 7,864.10^-13 J

E = 7,864.10^-13 / 1,602.10^-19 = 4,909.10⁶ eV = 4,909 MeV

10. Affirmation vraie.       A = 3,75.10³ Bq   pour  V_gaz = 1 m³   ;  l = 2,10.10^-6 s^-1
A = l.N  ;  N = A / l = 3,75.10³ / 2,10.10^-6 =1,79.10⁹ noyaux = 1,79.10⁹ / 6,02.10²³ » 3.10^-15  mol

 

©Sciences Mont Blanc