Correction Bac Liban Juin 2003

Calculatrice autorisée

 

I – Evolution temporelle de deux oscillateurs (9 points)

II - Pile cuivre-argent (3 points)

III – Etude de l'estérification (4 points)

 

Correction Liban Juin 2003 - I ) Evolution temporelle de deux oscillateurs

A ) Oscillateur mécanique :

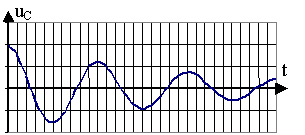
1)     L'enregistrement 3 correspond à des oscillations non amorties, il est donc obtenu dans le cas a) soufflerie à puissance maximale. Le régime est périodique.
L'enregistrement 1 correspond à des oscillations amorties faibles, il est donc obtenu dans le cas b) puissance de la soufflerie légèrement diminuée. Le régime est pseudo-périodique.
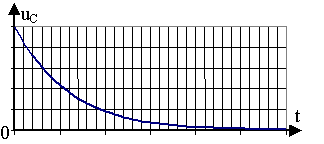
L'enregistrement 2 correspond à des oscillations fortement amorties, il est donc obtenu dans le cas c) puissance de la soufflerie fortement diminuée. Le régime est apériodique.

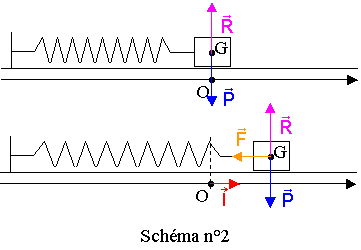
2)     a) forces exercées sur le solide S :
R : réaction normale du plan
P : poids du solide S
F : force de rappel du ressort

b) On applique la 2^ème loi de Newton dans le référentiel terrestre galiléen,
au système solide S : P + R + F = m. a _G

Projection sur l'axe Ox :  0 + 0 + F_x = m.a _x (1)

F_x = - k.x   Þ   (1)  – k.x = m.x'' = m.d²x/dt²

Þ m. d²x/dt² + k.x = 0

c) x = X_M.cos(2 p t / T₀ + F₀)    ; X_M est l'amplitude et F₀ est la phase à l'origine.
à t = 0 s , v_x = 0 m.s^-1   et x = 10,0 cm   ;  x = X_M.cos F₀ = x₀
v_x = dx/dt = - (2 p / T₀) . X_M.sin(2 p t / T₀ + F₀)   ;

à t = 0 s , dx/dt = - ( 2 p / T₀).X_M.sin F₀ = 0   Þ  sin F₀ = 0   Þ F₀ = 0 ou p
Si F₀ = 0 , x₀ = X_M  et si F₀ = p , x₀ = - X_M ce qui est impossible car x₀ > 0
Þ F₀ = 0    ;   x₀ = X_M = 10,0 cm = 0,1 m     ;   x = x₀.cos(2 p t / T₀)

d) On utilise l'enregistrement 3 car les frottements sont négligeables et les oscillations sont non amorties.
D'après l'enregistrement 3, une période T₀ vaut 1 s.

e) étudions les différentes propositions.
F = k. ½x½  ;  [ k ] = [ F / ½x½] = [m.a / ½x½] = M.L.S^-2 / L= M.S^-2

[2 p ( m / k )] = [ m / k ]^{1/ 2}  = M^{1/ 2} .(M.S^-2)^{-1/ 2} = M^{1/ 2} .M^{-1/ 2} .S¹ = S¹    
ceci est compatible avec un temps comme la période T₀ .

[2 p( k / m )] = [ k / m ]^{1/ 2}  =(M.S^-2)^{1/ 2} . M^{-1/ 2} = M^{1/ 2} . .S^-1 . M^{-1/ 2} = S^-1    
ceci est compatible avec l'inverse d'un temps . Cette formule est donc fausse .

[2 p m / k] = [ m / k ] = M .(M.S^-2)^-1 = M.M^-1.S² = S²   
ceci est compatible avec un temps au carré. Cette formule est donc fausse.

T₀ = 2p( m / k ) Þ T₀² / 4 p²= m / k  Þ  k = m.4 p²/ T₀² = 0,1 x 4 x 3,14² / 1,0² = 3,95 N.m^-1

3) a) Ep _élast. = ½ k.x²    ;   Ec = ½ m.v²    ;    E = Ep + Ec
b) à t = 0 s , x = X_M   ;  v = 0 m.s^-1   ;  E = ½ k.x² + ½ m.v² = ½ k.X_M² = ½ x 3,95 x 0,1² = 0,02 J

Au cours du mouvement , l'énergie mécanique E se converse, elle est constante.  E = 0,02 J

A la position d'équilibre, x = 0 m, Ep = 0 J  ,  E = Ec = ½ m.v²    
v = ( 2 E / m ) = ( 2 x 0,02 / 0,1) = 0,63 m.s^-1  

c)

 

 

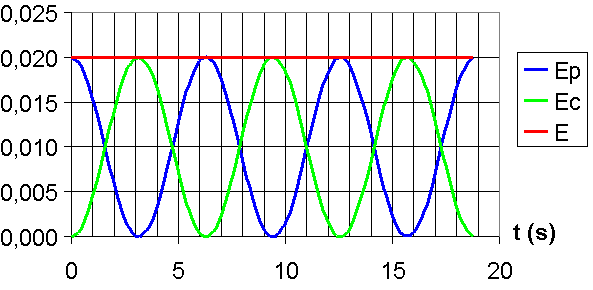On détermine facilement la courbe correspondante à l'énergie E car elle est constante.

Ensuite, on connaît les valeurs à t = 0 s , Ec = 0 J et Ep = E = 0,02 J.
Cela permet de distinguer les 2 autres courbes.

d) Dans un régime pseudo-périodique, l'énergie mécanique diminue car il y a de l'énergie dissipée par frottements.

 

B ) Application des oscillations électrique :

1)

Si la résistance R est faible, l'amortissement est faible, le régime est pseudo-périodique.	Si la résistance R est grande, l'amortissement est important , le régime est apériodique.

 

 

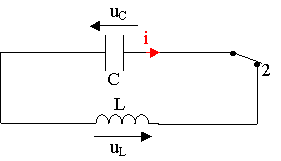2) R = 0 W. Elle disparaît du montage.

On choisit un sens de courant et on flèche les tensions en respectant la convention récepteur.

Loi des tensions dans le circuit :     u_C + u_L = 0  (1)

q = C.u_C   ;   i = dq/dt    ;   u_L = L.di/dt = L.d²q/dt²

On remplace dans la relation (1) :

q /C + L.d²q/dt² = 0   ou    q + LC.d²q/dt² = 0   (2)

 

3) q = Q_M.cos(2p.t / T₀ + f₀ )  ; dq/dt = - Q_M.(2p / T₀).sin(2p.t / T₀ + f₀ ) 

d²q/dt² = - Q_M.(2p / T₀)² .cos(2p.t / T₀ + f₀ )  .  On remplace dans la relation (2).

(2)  Q_M.cos(2p.t / T₀ + f₀ ) - L.C.Q_M.(2p / T₀)² .cos(2p.t / T₀ + f₀ ) = 0

(2)  Q_M.cos(2p.t / T₀ + f₀ ).[ 1 - L.C.(2p / T₀)² ] = 0

Pour que la relation (2) soit valable quelque soit l'intant t , il faut  : 1 - L.C.(2p / T₀)² = 0

(2p / T₀)² = 1 / (L.C)  Þ  T₀ / 2p = (L.C)  Þ  T₀ = 2p.(L.C)

L'expression proposée est bien une solution de l'équation différentielle avec T₀ = 2p.(L.C).

4) T = 31,4 ms  ;  L = 200 mH  ;    T² = 4p².L.C   Þ  C =T² / ( 4 p².L )

C = (31,4.10^-6)² / (4 x 3,14².200.10^-3 ) = 1,25.10^-10 F = 125 pF

5) a)  C = a.h + b         Pour cette relation, on choisit C en pF pour simplifier l'expression.

D'après les caractéristiques du capteur, si h varie de 1 %, la capacité C varie de 0,4 pF

DC = a.Dh  Þ a = DC / Dh = 0,4 / 1 = 0,4  ;

si h = 43 % d'HR , C = 122 pF = 43 a + b = 0,4 x 43 + b  Þ b = 122 - 0,4 x 43 = 104,8

Si C est en pF , on a :  C = 0,4 h +104,8

b) Dans l'expérience , la capacité C vaut 125 pF .

C = 0,4 h + 104,8   Þ  h = (C - 104,8 ) / 0,4 = (125 -104,8 ) / 0,4 = 50,5 % d'HR

 

©Sciences Mont Blanc

 

 

 

Correction Liban Juin 2003 - II ) Pile cuivre-argent

 

A)   Transformation chimique spontanée par transfert direct d'électrons :

1)     L'intensification de la coloration bleue indique la formation d'ions Cu²⁺ et le dépôt gris correspond à du métal Argent formé. IL s'agit donc de la réaction (1).

2)     Critère d'évolution spontanée : Si Q_r,i < K , l'évolution est dans le sens direct et si Q_r,i > K , l'évolution se fait en sens opposé .

3)     Equation : Cu_(s) + 2Ag⁺_(aq) = Cu²⁺_(aq) + 2Ag_(s) 
Q_r,i = [Cu²⁺]_i / [Ag⁺ ]_i² = (C₁/2) / (C₂/2)² = 0,5 / 0,25² = 8
Q_r,i < K₁ , le système évolue dans le sens direct.
Ceci est compatible avec les observations puisqu'on observe la formation des ions Cu²⁺ et de métal argent.

B) Constitution et fonctionnement de la pile cuivre-argent en circuit fermé

1)     Schéma

2) a) Le courant circule de l'électrode d'argent vers l'électrode de cuivre, et sort du pôle Å, qui est donc l'électrode d'argent, le pôle - est donc l'électrode de cuivre.
b) A l'électrode de cuivre : Cu_(s) = Cu²⁺_(aq) + 2 e^-
A l'électrode d'argent :  Ag⁺_(aq) + e^- = Ag_(s) 

c) Equation : Cu_(s) + 2Ag⁺_(aq) = Cu²⁺_(aq) + 2Ag_(s)

d) Si le système était en équilibre, il n'y aurait pas circulation d'électrons, pour que la pile fonctionne, il faut que Q_r,i ¹ K. Le système est hors équilibre.

 

           

©Sciences Mont Blanc

 

 

 

Correction Liban Juin 2003 III ) Etude de l'estérification :

 

n(ethanol)₀ =0,10 mol  ; n(ac.eth)₀ = 0,10 mol

1) CH₃–CH₂–OH + CH₃–COOH = CH₃–COO–CH₂–CH₃ + H₂O

L'ester est l'éthanoate d'éthyle

2) On refroidit rapidement les ampoules avant chaque dosage pour stopper l'estérification.

3) a)

Equation de la réaction		C2H5–OH+CH3–COOH = CH3–COO–C2H5+H2O
Etat du système	Avancement	Quantité de matière en mol
Etat initial	0	0,10	0,10	0	0
en cours	x	0,10 - x	0,10 - x	x	x
Etat final	xf	0,10 – xf	0,10 – xf	xf	xf

Si la réaction est totale, n(éthanol)_f = 0 = n(ethanol)₀ – x_max  ; 

x_max = n(ethanol)₀ = 0,10 mol = 100 mmol      ( ou même raisonnement avec l'acide éthanoïque )

b) D'après le tableau, n(CH₃–COOH)_f = 100 – x_f  Þ x_f = 100 – n   (en mmol)

4) t = x_f / x_max

Date t (en h)	0	4	10	20	40	100	150	200	250	300
Quantité de matière n (mmol)	100	75	64	52	44	36	35	34	33	33
Avancement final xf (mmol)	0	25	36	48	56	64	65	66	67	67
taux d'avancement t	0	0,25	0,36	0,48	0,56	0,64	0,65	0,66	0,67	0,67

5)

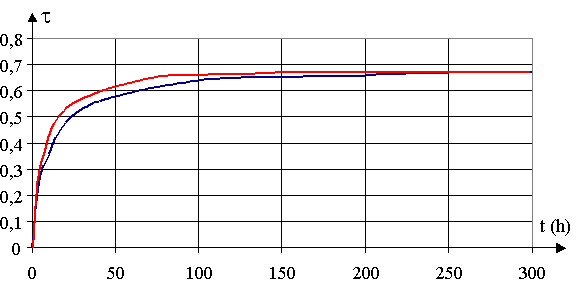La courbe rouge est celle correspondant à une température plus élevée.

6) La courbe montre que la transformation est lente et limitée par l'hydrolyse de l'ester ( x_f < 1 )

7) Si on augmente la température, la transformation est plus rapide mais l'état d'équilibre n'est pas modifié, t_f reste à 0,67 . La température est un facteur cinétique.

 

©Sciences Mont Blanc