Correction Bac Pondichéry Avril 2003

Calculatrice autorisée

 

I ) Etude d'une estérification (6 points)

II) Mise en orbite d'un satellite artificiel par la fusée Ariane (6 points)

III ) Le flash électronique (4 points)

III ) (spe) Le flash électronique (4 points)

 

Correction Pondichéry Avril 2003 - I ) Etude d'une estérification :

1) a) CH₃–COOH +  CH₃–CH₂–CH₂–OH = CH₃–COO–CH₂–CH₂–CH₃ + H₂O

L'ester formé est l'éthanoate de propyle

b) n(alcool) = m(alcool) / M(alcool) =  r(alcool).V(alcool) / M(alcool)

V(alcool) = n(alcool).M(alcool) / r(alcool) = 0,500 x ( 3 x 12 + 1 x 16 + 8 x 1) / 0,80 = 37,5 mL

c) n(acide)₀ = n(acide)_restant + n(acide)_réagi  ;  n(acide)_réagi = n(acide)₀ – n(acide)_restant

D'après l'équation, n(acide)_réagi = n(ester)_formé .

n(ester)_formé = n(acide)₀ – n(acide)_restant = 0,500 – n(acide)_restant

 

2) a) CH₃–COOH_(aq) +  HO^-_(aq)  ® CH₃–COO^-_(aq) + H₂O_(l)

b) La constante d'acidité de l'acide éthanoïque est la constante d'équilibre de la réaction entre l'acide éthanoïque et l'eau. 

K = Q_r,éq = [CH₃–COO^-]_éq / ([CH₃–COOH]_éq.[HO^-]_éq) 

K = [CH₃–COO^-]_éq.[H₃O⁺]_éq / ([CH₃–COOH]_éq.[HO^-]_éq.[H₃O⁺]_éq) = K_A / K_e = 10^-4,8 / 10^-14 = 10^9,2

K > 10⁴ , on peut donc considérer la réaction de titrage comme totale.

c) D'après l'équation de dosage, n(acide)_dosé = n(HO^-)_versé = c_b.V_E = 1,0 x 14,2.10^-3 = 1,42.10^-2 mol

n(acide)_erlenmeyer = n(acide)_dosé . V_fiole /V_prélevé = 1,42.10^-2 x 100.10^-3 / 5.10^-3 = 0,284 mol   ( n°1)

n(ester)_formé = 0,500 – n(acide)_restant = 0,500 – 0,284 = 0,216 mol

(cela correspond au graphique de l'annexe 1)

 

3) a)

Equation chimique		CH3–COOH    +      C3H7–OH    =  CH3–COO–C3H7 + H2O
Etat du système	Avancement	Quantité de matière en mol
Etat initial	0	0,500	0,500	0	0
En cours	x	0,500 - x	0,500 – x	x	x
Etat final	xf	0,500 – xf	0,500 - xf	xf	xf

Si la réaction était totale, les réactifs étant dans les proportions stœchiométriques, leurs quantités finales seraient nulles : n(acide)_f = n(alcool)_f = 0 = 0,500 – x_max = 0  Þ  x_max = 0,500 mol

D'après l'annexe 1, x_éq = 0,325 mol.    x_éq < x_max

rendement r = n(ester)_formé / n(ester)_max = x_éq / x_max = 0,325 / 0,500 = 0,65 = 65 %

b) v = ( 1 / V ) dx/dt

La vitesse volumique d'une réaction représente la pente de la tangente de la courbe.

D'après l'annexe 1, on constate que cette vitesse est grande au début et diminue jusqu'à s'annuler lorsque l'équilibre est atteint. Elle diminue car les quantités de réactifs diminuent.

c) K' = Q_{r, éq} = [ester]_éq.[H₂O]_éq / ([alcool]_éq.[acide]_éq) = (x_éq /V) ² / ((0,500 – x_éq)/V)²

K' = 0,325² / (0,500 – 0,325)² = 3,45

d) Q_r = [ester].[H₂O] / ([alcool].[acide]) = n(ester).n(H₂O) / (n(alcool).n(acide))

Q_r = 0,325² / (0,175 x 1,175) = 0,51

Q_r < K' , le système évolue donc dans le sens direct de la réaction, de la formation de l'ester.

K' = x_éq² / ((0,500 – x_éq).(1,50 – x_éq)) = 3,45

3,45 ( 0,75 – 2 x_éq + x_éq²) = x_éq²   Þ   2,59 – 6,9 x_éq + 2,45 x_éq² = 0

1,06 – 2,82 x_éq + x_éq² = 0  ;  D = b² – 4 a.c = 2,82² – 4 x 1,06   ;  D = 3,69           ;  D = 1,92

x₁ = (- b + D) / 2a = ( 2,82 + 1,92 ) / 2 = 2,37  ; impossible car  x₁ > x_max

x₂ = (- b - D) / 2a = ( 2,82 - 1,92 ) / 2 = 0,45 

x_éq = 0,45  ;   r = x_éq / x_max = 0,45 / 0,500 = 0,90 = 90 %

©Sciences Mont Blanc

 

 

 

Correction Pondichéry Avril 2003 - II ) Mise en orbite d'un satellite artificiel par la fusée Ariane :

 

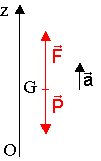a)  F : force de poussée des réacteurs , verticale vers le haut , F = 2445 kN

     P : poids de la fusée, verticale vers le bas , P = m.g₀ = 208.10³ x 9,8 = 2038 kN

b) On applique la 2^ème loi de Newton dans le référentiel terrestre galiléen au système satellite.     F + P = m.a

Projections sur un axe Oz vertical vers le haut :  F - m.g₀ = m.a  Þ  a = F/m -g₀.

c) m₁ = m = 208.10³ kg ;    a₁ = 2445.10³ / 208.10³ - 9,8 = 1,95 m.s^-2

m₂ = 208 - 147,5 = 60,5 T = 60,5.10³ kg   ;   a₂ = 2445.10³ / 60,5.10³ - 9,8 = 30,6 m.s^-2 

a₂ >a₁ ;  l'accélération n'est pas constante : le mouvement n'est pas uniformément accéléré.

d) v_e = F / (Dm/Dt)     ;    v_e = F x Dt / Dm

D'après la 2^ème loi de Newton, force = masse * accélération ;  une force est en kg.m.s^-2

F Dt /D m est en kg.m.s^-2.s.kg^-1 , soit m.s^-1 .  v_e a donc une unité en m.s^-1

v_e = F x Dt / Dm = 2445.10³ x 145 / 147,5.10³ = 2403 m.s^-1

D m est négatif, car la masse de la fusée diminue ; Dt positif ;

v_e  et F sont colinéaires mais de sens contraire ; F est vers le haut ; v_e est vers le bas.

v _e est vers le bas car les gaz sont éjectés vers le bas.

D'après le principe des interactions ( 3^ème loi de Newton), si un corps A (fusée) exerce sur un corps B ( gaz éjectés) une force F_{A / B} , inversement, B exerce sur A une force opposée F_{B / A}  telle que : F_{A / B} = - F_{B / A}.

La fusée expulse les gaz vers le bas avec une force F_{f / g} , on a alors les gaz qui exercent une force sur la fusée F_{g / f}  opposée vers le haut.

2) a) On utlise le repère de Frenet :   a = a_N + a_T = v²/r u_N + dv/dt u_T .
v est constante. dv/dt  = 0, a_T = 0 , a = a_N = v²/r u_N . L'accélération est centripète, perpendiculaire à la trajectoire circulaire vers le centre O.

b) Loi de gravitation universelle:

Soit deux corps A et B de masse m_A et m_B distant de AB , les deux corps exercent l'un sur l'autre des forces attractives : F_{A / B} = F_{B / A} = G.m_A.m_B / AB²

 

c) r = R_T + h  ;  F_S = m_S. g(h) 

F_S = m_S. g(h) = G.M_T.m_S / (R_T + h )²  Þ g(h) = G.M_T /(R_T+h)²

g₀ = g(0) = G.M_T / R_T² ; soit GM_T= g₀ R_T²   ;  g(h) = g₀ R_T²/(R_T+h)²

d) Dans le référentiel galiléen géocentrique, on applique la 2^ème loi de Newton au système satellite 

         F_S = m_S.a   (1)

On utilise la base de Frenet : a = a_N + a_T = v_S²/r u_N + dv_S/dt u_T = v_S²/r u_N   et  F_S = F_S.u _N

(1) m_S.v_S²/r u_N  = F_S.u _N   Þ m_S.v_S²/r = F_S = m_S.g(h)   Þ   v_S²/r = g(h) = G.M_T /r²

d'où v_S² = G.M_T / r     ; v_S = R_T. g₀/r

La période T_S est la durée nécessaire pour parcourir un périmètre 2 p r à la vitesse v_S :

v_S = 2 p r / T_S    ;    T_S = 2 p  r / v_S = 2 p (R_T+h)^{3 / 2} /(R_T.g₀)

e) r = (6400+200) 10³ = 6600.10³ m

v_s = 6400.10³ x 9,8 / 6600.10³ = 7800 m.s^-1 

T_S = 2 p r / v_S = 2 x 3,14 x 6600.10³ / 7800 = 5320 s = 1h 28 min 40 s

        

 

©Sciences Mont Blanc

 

 

 

Correction Bac Pondichéry Avril 2003 - III ) Le flash électronique :

I ) Etude du flash :

1) E_e = ½ C.u_C² = ½ 150.10^-6 x 330² = 8,17 J

2) P_e = E_e / t = 8,17 / 1.10^-3 = 8,17.10³ W

3) Si on n'élève pas la tension, le condensateur n'emmagasine pas assez d'énergie et la puissance est alors insuffisante pour créer un éclair :
Si U = 3 V , E_e = ½ 150 10^-6 x 3² = 6,75 10^-4 J ; P_e = 0,675 W.

II ) Etude expérimentale du circuit RC :

1)     Si le condensateur est déchargé à t = 0, q = 0 C et u_C = 0 V.
D'après le schéma du montage, u_G = u_R + u_C  Þ  E = R.i + 0 
Þ R = E / i = 12 / 54,0.10^-6 = 2,22.10⁵ W

2)      

 

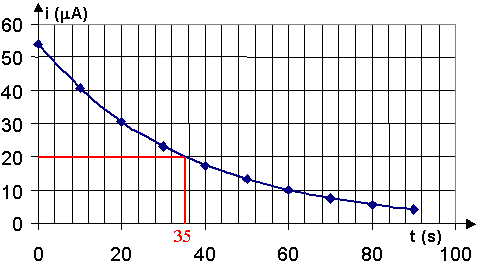3)     i(t) = I₀.e ^{–t / t} ;     i(t) = I₀.e^-1 = 54,0 x 0,368 = 19,9 mA .  D'après le graphique, t = 35 s
t = R.C  ;  C = t / R = 35 / 2,22.10⁵ = 1,58.10^-4 F = 158 mF
Ce résultat est conforme aux indications du fabricant :  158 mF < 150 mF +10%

 

 

©Sciences Mont Blanc

 

 

 

Correction Pondichéry Avril 2003 - III ) Le télescope de Newton :

 

I ) Images d'un objet réel AB dans un miroir plan et un miroir sphérique

 

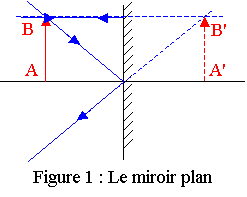
a) L'image A'B' de la flèche AB dans le miroir plan est son symétrique par rapport au miroir..

g = A'B' / AB = 1

 

 

 

 

 

b) L'objet AB étant situé à l'infini sur l'axe D, son image est située dans le plan focal image du miroir sphérique (passant par F et perpendiculaire à D).

 

Sur la figure 2, l'objet AB n'est pas à l'infini.

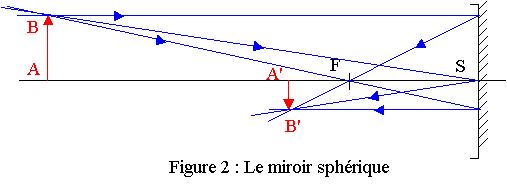
II ) Étude du télescope

a) L'image F₁' de F₁ dans le miroir plan est le symétrique de F₁ par rapport au miroir plan.
IF₁ = IF₁'

On place l'oculaire de telle façon que F₂ soit confondu avec F₁' pour le télescope soit afocal.

L'image finale est à l'infini car l'objet A₂B₂ est dans le plan focal objet de l'oculaire.

 

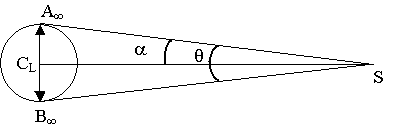b) Le diamètre apparent est l'angle q avec lequel l'objet est vu à l'œil nu.

C'est l'angle entre A_¥S et B_¥S 

a est l'angle entre l'axe D et A_¥S  .

Par symétrie, l'angle entre D et B_¥S est a.

On a donc 2 a = q

 

 

A_∞ étant à l'infini, son image A₁ pour le miroir sphérique est dans le plan focal image du miroir sphérique.

 

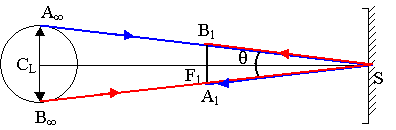
tan a = A₁F₁/ F₁S = (A₁B₁/2)/ f₁ = A₁B₁/2f₁  a étant petit,

tan a » a » q / 2 Þ q »  A₁B₁ / f₁

Ce schéma n'est pas à l'échelle.

 

 

 

A₂ et B₂ sont les symétriques de A₁ et B₁ par rapport au miroir plan. Par symétrie, A₂B₂ = A₁B₁

A₂B₂ = A₁B₁ = q . f₁  = 0,00872 x 1,20  = 1,05.10^-2 m = 1,05 cm

 

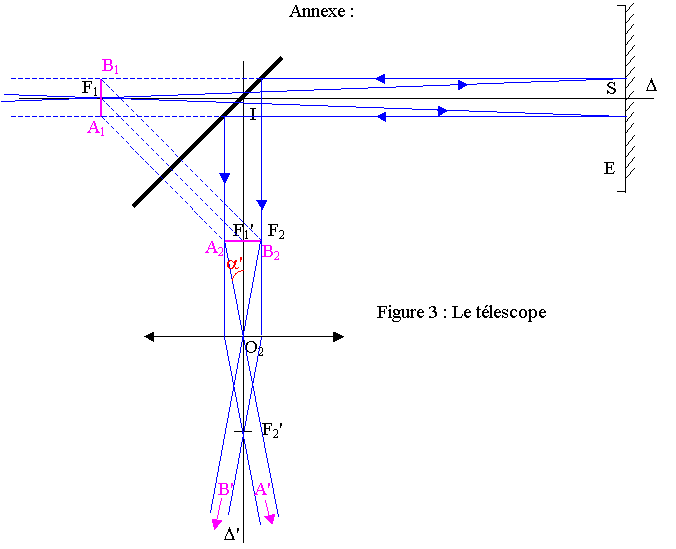
c) Pour placer A₂B₂ sur la figure 3, il faut d'abord placer A₁B₁ . On sait que A₁ et B₁ sont dans le plan focal image du miroir sphérique, il suffit donc de tracer un seul rayon venant de A_¥ (passant par F₁' réfléchi parallèle à l'axe D) pour obtenir A₁ et un autre pour B₁. Attention les rayons déjà tracés sur la figure 3 ne peuvent pas être utilisés pour trouver A₁ et B₁ car étant parallèle à D, ils ne peuvent venir des points A_¥ et B_inf . En effet les rayons parallèles à l'axe D venant de A _inf et B_inf  ne rentrent pas dans le télescope . Pour placer A₂ et B₂ , on prend les symétriques de A₁  et B₁ par rapport au miroir plan.

 

L'objet A₂B₂ étant dans le plan focal objet, l'image de la Lune dans l'oculaire est à l'infini.

 

tan a' = A₂F₂ / F₂O₂ = (A₂B₂ / 2) / f₂' » a' Þ 2 a' » A₂B₂ / f₂'

A₁B₁ » q . f₁ » 2 a . f₁ » A₂B₂   Þ a' » a . f₁ / f₂'  

D'après la figure 3, q » A₂B₂ / f₂' Þ q » 2 a'

 

d) q' / q = a' / a =  f₁ / f₂' = 1,20 / 2,00.10^-2 = 60,0

Ce quotient est appelé grandissement. La valeur de 60 indique bien que le télescope agrandit par rapport à la vision à l'œil nu et cela justifie le terme agrandissement.

 

 

©Sciences Mont Blanc