Correction Sujet Bac Amérique du nord Juin 2003

Calculatrice autorisée

Correction Amérique du nord Juin 2003 - I ) Quelques propriétés de l'acide salicylique

Partie A : Etude de la fonction acide

I ) Etude théorique :

1) a) HA_(aq) + H₂O_(l) = A^-_(aq) + H₃O⁺_(aq)

b) n₀(HA)= C.V

Equation de la réaction		HA_(aq) + H₂O_(l) = A^-_(aq) + H₃O⁺_(aq)
Etat du système	Avancement (mol)	Quantité de matière en mol
Etat initial	0	C.V	excès	0	0
en cours	x	C.V – x	excès	x	x
Etat final	x_f	C.V – x_eq	excès	x_eq	x_eq

[H₃O⁺]_eq = [A^- ]_eq= x_eq / V

[HA]_eq = (C.V – x_eq) / V = C – [H₃O⁺]_eq

Q_{r,
eq} = [H₃O⁺]_eq.[A^- ]_eq/ [HA]_eq = [ H₃O⁺ ]_eq² / (C – [H₃O⁺]_eq)

2) s = l₁.[H₃O⁺]_eq + l₂.[A^-]_eq = (l₁ + l₂).[H₃O⁺]_eq

II ) Etude expérimentale

1) Il faut diluer par dix la solution S₀ .

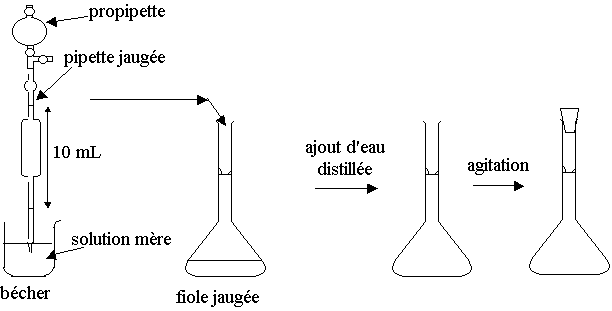On verse la solution S₀ dans un bécher de 50 mL pour en prélever 10 mL à l'aide de la pipette jaugée de 10 mL, surmontée du pipeteur. On verse les 10 mL dans une fiole jaugée de 100 mL et on complète avec de l'eau distillée jusqu'au trait de jauge, puis on agite pour homogénéiser la solution. n(HA)_avant = n(HA)_après Þ C.V = C₀.V₀ Þ C = C₀.V₀ / V = C₀ / 10 (dilution par 10 )

2) Mesures de conductivité

a) s = (l₁ + l₂).[H₃O⁺]_eq ; [H₃O⁺]_eq = s / (l₁ + l₂)

Q_{r,
eq} = [ H₃O⁺ ]_eq² / (C – [H₃O⁺]_eq) = (s / (l₁ + l₂))² / ( C - s / (l₁ + l₂))

[H₃O⁺]_eq = 7,18.10^-2 / (35,0.10^-3 + 3,62.10^-3) = 1,86 mol.m^-3 = 1,86.10^-3 mol.L^-1

Q_{r,
eq} = (1,86.10^-3)² / (5,00.10^-3 – 1,86.10^-3) = 1,10.10^-3 ; - log Q_{r, eq} = 2,96

b) A concentration égale, l'acide salicylique est plus dissocié que l'acide benzoïque, le taux d'avancement final de la réaction avec l'eau est plus grand.

L'acide salicylique est plus fort que l'acide benzoïque.

c) La constante d'acidité K_A est la constante d'équilibre de la réaction entre l'acide et l'eau :

HA_(aq) + H₂O_(l) = A^-_(aq) + H₃O⁺_(aq) K_A = Q_{r, eq} = [ H₃O⁺ ]_eq² / (C – [H₃O⁺]_eq)

pK_A(ac.salicylique) = - log Q_{r, eq} » 3,0 et pK_A(ac.benzoïque) = - log Q_{r, eq} » 4,2

Ces valeurs correspondent à celles données dans l'énoncé.

Partie B – Synthèse de l'aspirine

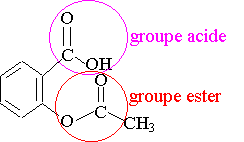1) La molécule comporte un groupe acide carboxylique et un groupe ester

2) a) A est l'acide éthanoïque CH₃-COOH

B est une molécule d'eau.

b) La réaction est une estérification.

Elle est lente, limitée et athermique.

©Sciences Mont Blanc

Correction Amérique du nord Juin 2003 - II ) Chute d'une balle de ping-pong

1) A l’instant initial, la force de frottement fluide F est nulle, car la balle est supposée lâchée sans vitesse initiale . Le schéma de Benoît correspond à l’instant initial.

Plus le temps de chute est long, plus la vitesse croît, plus F augmente : le schéma d’Adrien correspond à une date t quelconque, avant d’atteindre la vitesse limite.

Le schéma d’Amélie correspond à un temps de chute plus grand.

2) poids de la balle P = m . g = 2,3.10^-3 x 9,8 = 0,0225 N

poussée d’Archimède : p = m_air . g = r . V_S . g = 1,3 x ( 4/3 p x (1,9.10^-2)³) = 3,66.10^-4 N

P / p = 0,0225 / 3,66.10^-4 = 61,6

On peut donc négliger la poussée d'Archimède devant le poids de la balle. Benoît a raison.

3) Soit un axe (O, k ) orienté vers le bas .

On applique la 2^ème loi de Newton dans le référentiel terrestre galiléen au système balle :

Les forces extérieures exercées sur la balle sont : le poids P vertical vers le bas, P = m.g

et la force de frottement fluide F verticale vers le bas opposée au déplacement.

2^ème loi : P + F = m. a. Projection sur l'axe ( O, k) : P - F = m.a Þ m.g - F = m. dv/dt (1)

4) La balle a été lâchée sans vitesse initiale (v₀ = 0), et tend vers une vitesse limite : la vitesse v est représentée par la courbe 2. La courbe 1 est celle traduisant l’évolution de l’accélération : lorsque la vitesse limite est atteinte, a doit s’annuler et elle diminue au cours du temps.

5) D'après la courbe 2, v_lim = 8 m.s^-1 . Lorsque la vitesse limite est atteinte, a = dv/dt = 0. L’équation (1) donne : 0 = m.g - F = m.g - k.v_lim²

k = m.g / v_lim² = 2,3.10^-3 x 9,8 / 8² = 3,52.10^-4 U.S.I.

k / m = 0,15 ; dv/dt = g - k/m v² Þ dv/dt = 9,8 - 0,15 v² (2)

6) k_t = 0,22 .p .r.r² = 0,22 x 3,14 x 1,3 x (1,9.10^-2)² = 3,24.10^-4 U.S.I.

écart = ½ k - k_t½ / k_t = 8,6 % . La valeur théorique s’accorde avec la valeur expérimentale .

7)a) Le temps caractéristique de l’évolution du système peut s’évaluer par l’intersection entre l’asymptote horizontale (pour t > 2 s) et la tangente à l’origine. Graphiquement, t_C = 0,85 s.

Un bon pas d’itérations est proche de t_C / 100 . En réalité, on peut se contenter de t_C/ 20 ,

soit 0,0425 s. Le pas choisi semble convenable ; il est cependant un peu trop grand pour permettre de décrire (numériquement) de manière fine l’évolution temporelle du système.

b) équation (2) : dv/dt = 9,8 - 0,15 v² . Dv = ( 9,8 - 0,15 . v_i² ).Dt ; v₀ = 0 m.s^-1

t₁=0,05s ; v₁ = v₀ + Dv = v₀ + ( 9,8 - 0,15 . v₀² ).Dt = 0 + 9,8 x 0,05 = 0,49 m.s^-1

a₁ = 9,8 - 0,15 . v₁² = 9,76 m.s^-2

t₂ =0,1s ; v₂ = v₁+Dv = v₁+( 9,8 - 0,15 . v₁² ).Dt = 0,49 + ( 9,8 - 0,15 x 0,49²)x 0,05 = 0,98 m.s^-1

a₂ = 9,8 - 0,15 . v₂² = 9,66 m.s^-2

t₃ =0,15s ; v₃ =v₂+Dv = v₂+( 9,8 - 0,15.v₂² ).Dt = 1,46 m.s^-1 ; a₃ = 9,8 - 0,15 . v₃² = 9,48 m.s^-2

c) La présentation des résultats dans le tableau « par Adrien » est aberrante, car les calculs se font avec 2 ou 3 chiffres significatifs au maximum. On ne peut accorder aucune signification à tous les chiffres que présente Adrien.

8) a) On constate que les courbes sont relativement similaires et les simulations reproduisent assez bien l’évolution de la vitesse et de l’accélération. Cependant, on peut remarquer que la méthode d’Euler ne converge pas bien car l’accélération ne tend pas vers 0 assez rapidement.

b) On peut refaire le calcul numérique avec un pas plus petit que 0,05 s .

c) On peut envisager une loi en F = k.v, qui évolue moins rapidement avec v.

L’équation (2) s’écrit alors : m.dv/dt = m.g - k.v Þ dv/dt = g - k.v /m

Si v_lim est atteint, dv/dt = 0 , 0 = g - k.v_lim / m Þ k = 2,82.10^-3 U.S.I. , k/m = 1,22

équation (2) : dv/dt = 9,8-1,22 v

©Sciences Mont Blanc

Correction Amérique du nord Juin 2003 - III ) Dipôle RLC :

A) Première expérience

1) Le phénomène observé sur la voie 1 à la fermeture de K est la charge du condensateur.

3) u₁(t) = 0,63.u_{1 max} = 0,63.E = 3,8 V. D'après le graphique, t = 0,4 ms

t = R.C Þ C = t / R = 0,4.10^-3 / 20

t = 2,0.10^-5 F = 20 mF

4) a) Loi d'additivité des tensions :

E = u_R + u₁

u_R = R.i ; i = dq / dt et q = C.u₁

i = C.du₁/dt

E = R.C.du₁/dt + u₁ = t.du₁/dt + u₁

b) u₁ = E.( 1 – e ^{- t /}^t ) ;

u₁(5t) = E.( 1 – e^–5 ) = 0,993.E = 5,96 V à t = 5 t, on peut considérer que la charge est complète.

B ) Deuxième expérience

1) La courbe 1 vaut 6 V à t = 0 s, puis diminue. Il s'agit donc de la tension u₁ aux bornes du condensateur, qui au départ est complètement chargé (sous une tension de 6 V) et se décharge.

La courbe 2 correspond à la tension aux bornes du conducteur ohmique. A t = 0s, u = 0 V car l'intensité est nulle.

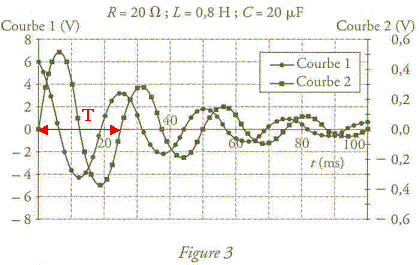2) D'après la figure 3, la pseudo-période T vaut 25 ms. On trouve cette durée au passage de la tension par zéro dans le même sens de variation.

T₀ = 2 p.(L.C) = 2 x 3,14 x (0,8 x 20.10^-6 ) = 0,0251 s » 25 ms.

La pseudo-période est très proche de la période propre.

3) En diminuant la valeur de L, la valeur de la pseudo-période T diminue aussi, il s'agit de la figure 5 et en augmentant la valeur de C, la pseudo-période T augmente, ce qui correspond à la figure 4.

Correction Sujet Bac Amérique du nord Juin 2003 - III ) Modélisation du principe du microscope :

I ) Etude de l'objectif :

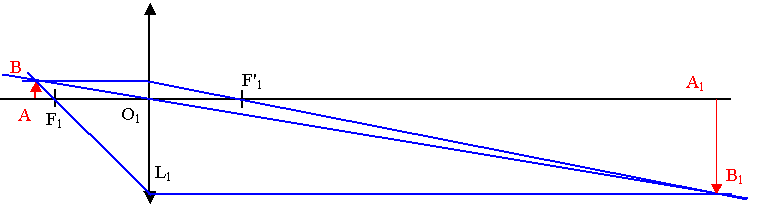
2) formule de conjugaison : 1//Å₁ – 1/ /Å = 1/f₁ Þ 1//Å₁= 1/5 + 1/(-6) = 1/30 Þ /Å₁= 30 cm

g₁= Å₁B₁ / ÅB = /Å₁ / /Å = 30 / (-6) = - 5 Þ Å'B' = - 5 ÅB = - 5 x 0,5 = - 2,5 cm

3) Ces mesures sont compatibles avec les valeurs calculées , les différences correspondent aux erreurs d'expériences

(image nette, lecture des distances).

4) Dans ce cas, l'objet est entre O₁ et F₁, l'image obtenue est virtuelle et ne peut pas être observée sur un écran.

II ) Etude de l'oculaire :

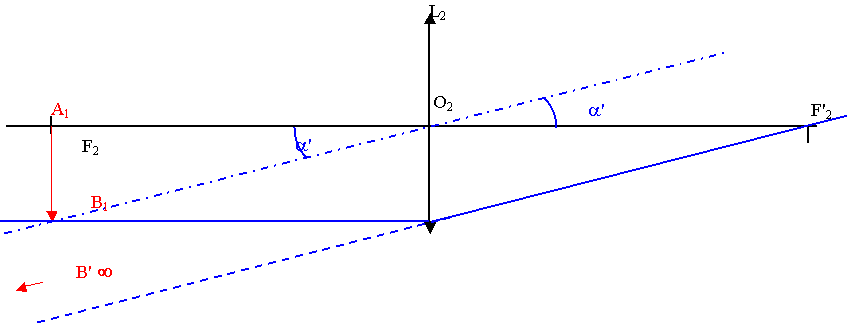
1) Pour que l'image A₂B₂ donnée par L₂ soit à l'infini, il faut que l'objet A₁B₁ soit dans le plan focal objet de L₂ .

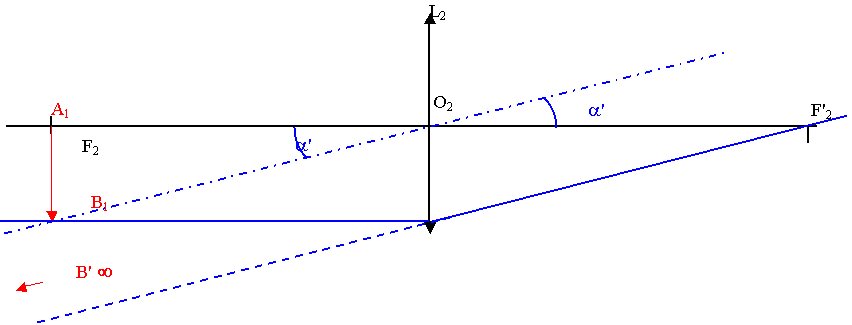
III ) Grossissement du microscope :

1) Si a est petit, tan a » a . tan a' = A₁B₁ / A₁O₂ = 2,5 / 20 = 0,125 Þ a' » 0,125 rad

2) tan a = AB / d = 0,5 / 25 = 0,02 Þ a » 0,02 rad

3) G = a' / a = 0,125 / 0,02 = 6,25

4) G_c = C₂.½g₁½.d = (1/20.10^-2) x 5 x 25.10^-2 = 6,25 = G