Correction Bac Afrique Juin 2004

Calculatrice autorisée

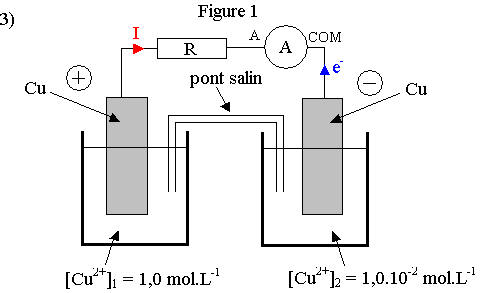
I ) Pile de concentration :

1) A l'électrode 1 positive , il y a une réduction : Cu²⁺_(aq) + 2 e^- = Cu_(s)

A l'électrode 2 négative , il y a une oxydation : Cu_(s) = Cu²⁺_(aq) + 2 e^-

Bilan : Cu_(s) + Cu²⁺_(aq) = Cu²⁺_(aq) + Cu_(s) K = 1

2) a) Quotient réactionnel initial : Q_{r, i} = [Cu²⁺ ]₂ / [Cu²⁺ ]₁ = 1,0.10^-2 / 1,0 = 1,0.10^-2

b) Q_{r,
i} < K . D'après le critère d'évolution spontanée, le système chimique dans le sens direct de l'équation. La valeur de Q_{r, i} est donc cohérente avec la polarité proposée.

Les concentrations finales restent constantes quand l'équilibre est atteint.

Q_{r, éq} = [Cu²⁺ ]₂ / [Cu²⁺ ]₁ = 1,0 Þ [Cu²⁺ ]₂ = [Cu²⁺ ]₁

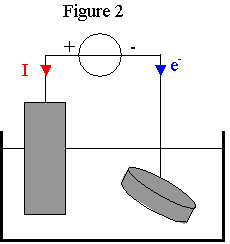
II ) Dépôt de cuivre par électrolyse :

1) a) Pour réaliser une électrolyse, il faut brancher un générateur aux bornes du système chimique.

b) Le générateur impose une tension au système chimique qui va évoluer en sens inverse de la réaction spontanée.

Les électrons sortent de la borne – du générateur.

A l'électrode reliée à la borne – du générateur, il y a une réduction : Cu²⁺_(aq) + 2 e^- = Cu_(s)

A l'électrode reliée à la borne + du générateur, il y a une oxydation Cu_(s) = Cu²⁺_(aq) + 2 e^-

c) Le courant sort de la borne + du générateur, circule dans le circuit et revient vers la borne -.

Les électrons circulent en sens inverse. L'électrode + est reliée à la borne + du générateur et l'électrode – est reliée à la borne – du générateur.

2) a) Q = I . t = 0,400 x 1 x 60 x 60 = 1440 C

b) Q = n(e^-).F Þ n(e^-) = Q / F = 1440 / 96500 = 1,49.10^-2 mol

c) D'après la demi-équation, n(e^-) = 2 n_disp(Cu²⁺)

d) n_dép(Cu) = n_disp(Cu²⁺) = n(e^-) /2 = 7,45.10^-3 mol

e) m(Cu) = n(Cu) . M(Cu) = 7,45.10^-3 x 63,5 = 0,473 g

III ) Détermination d'une concentration en ions cuivre II :

Equation chimique		2 Cu²⁺_(aq) + 4 I^-_(aq) = 2 CuI_(s) + I_{2 (aq)}
Etat initial	Avancement x = 0	n₀	excès	0	0
Etat intermédiaire	x	n₀ – 2x		2x	x
Etat final	x_max	n₀ – 2 x_max		2 x_max	n₁ = x_max

On suppose la réaction totale, cela est indispensable pour toute réaction de dosage.

Le réactif limitant Cu²⁺ est complètement consommé à l'état final : n₀ – 2 x_max = 0 Þ x_Max = n₀ / 2

n₁ = x_max = n₀ / 2

2) a) Le diiode a une couleur jaune-orange. Au cours du dosage, la solution se décolore peu à peu, lorsque la coloration est jaune pale , on peut ajouter de l'emplois d'amidon pour obtenir une coloration bleu foncé plus visible. Lorsque la solution est incolore, on a atteint l'équivalence.

b) A l'équivalence, les réactifs ont été mélangés dans les proportions stoechiométriques de l'équation. On a alors : n(S₂O₃^2-)_éq = 2 n(I₂)₀ = 2 n₁ (d'après l'équation)

c) n₁ = n(S₂O₃^2-)_éq / 2 = c.V_éq / 2 = 1,0.10^-1 x 10,0.10^-3 / 2 = 5,0.10^-4 mol

d) n₀ = 2 n₁ = 1,0.10^-3 mol

e) C₀ = n₀ / V₀ = 1,0.10^-3 / 0,100 = 1,0.10^-2 mol.L^-1

©Sciences Mont Blanc

Afrique Juin 2004 - II ) Datation au carbone 14 :

I ) Etude du noyau :

1) A est le nombre de masse, il correspond au nombre de nucléons du noyau.

Z est le numéro atomique, c'est le nombre de protons du noyau.

X est le symbole de l'élément chimique.

2) Symbole de l'atome du carbone 14 : : ¹⁴₆C

3) Le noyau de l'atome de carbone 14 contient 6 protons (Z=6) et 8 neutrons ( A-Z = 8)

4) Des isotopes sont des atomes ayant le même numéro atomique Z , même nombre de protons et un nombre de neutrons différent (A différent).

5) Un noyau radioactif est un noyau instable dont la désintégration (destruction) provoque l'apparition d'un nouveau noyau, l'émission d'une particule notée a, b ^- ou b ⁺, et fréquemment l'émission d'un rayonnement électromagnétique noté g .

II ) Les réactions nucléaires :

1) Le bombardement des noyaux d'atomes d'azote par les neutrons aboutit à la réaction nucléaire dont l'équation est la suivante : ¹⁴₇N + ¹₀n ® ^A_ZY₁ + ¹₁H (1)

a) Lois de Soddy : Lors d'une désintégration nucléaire, il y a conservation du nombre de charge Z et du nombre de nucléons A

b) D'après les lois de Soddy, on peut écrire : 14 + 1 = A + 1 Þ A = 14

et 7 + 0 = Z + 1 Þ Z = 6.

L'élément associé à Y₁ est donc du carbone 14 : ¹⁴₆C

2) a) ¹⁴₆C ® ⁰_-1e + ¹⁴₇N
Pour déterminer Z et A , on applique les lois de Soddy : 14 = 0 + A et 6 = -1 + Z

b) L'émission d'un électron ou particule b^- correspond à une désintégration b^-.

c) Y₂ est un élément azote.

III ) La loi de désintégration radioactive :

1) Le temps de demi-vie ( notée t_1/2) est la durée au bout de laquelle la moitié des noyaux radioactifs ont été désintégrés.

2) a) N(t) est le nombre de noyaux radioactifs présents à l'instant t.

N₀ est le nombre de noyaux radioactifs présents initialement.

l est la constante radioactive.

b) Analyse dimensionnelle : [l] = [ln2 / t_1/2] = T^-1 . L'unité de l est donc en seconde^-1 ou en an^-1 selon l'unité de t_1/2.

c) l = ln2 / t_1/2 = 0,69 / 5570 = 1,24.10^-4 an^-1

IV ) Application à la datation :

1) L'activité d'un échantillon de bois diminue au cours du temps car des noyaux se désintègrent au cours du temps.

2) a) t = (1/l).ln(A₀/A(t))

b) t = (1/1,24.10^-4).ln(13,6 / 12,0) = 1010 ans

c) L'année de construction du bateau est donc 973 ans (1983 – 1010)

d) L'hypothèse faite précédemment est donc vérifiée.

©Sciences Mont Blanc

Afrique Juin 2004 - III ) Tir au pigeon d'argile :

I ) Etude du mouvement du pigeon d'argile :

1) Le poids P_P force exercée par la Terre sur le pigeon est vertical vers le bas.

On applique le théorème du centre d'inertie ( 2^ème loi de Newton) au pigeon dans le référentiel terrestre supposé galiléen :

m_P . a_P = P_P = m_P . g Þ a_P = g

2) a_Px = g_x = 0 ; a_Py = g_y = - g

3) a_Px = dv_Px/dt Þ v_Px(t) = 0 + v_P0x = v_P0.cos a ;

a_Py = dv_Py/dt a_Py = dv_Py/dt

4) v_Px = dx_P/dt Þ x_P(t) = v_P0.cos a .t + x_P0 = v_P0.cos a .t ;

v_Py = dy_P/dt Þ y_P(t) = - ½ g.t² + v_P0.sin a .t + y_P0 = - ½ g.t² + v_P0.sin a .t

II ) Tir réussi :

1) La trajectoire de la balle est verticale. L'abscisse x de la balle est donc constante et égale à OA.

L'abscisse x_C du point d'impact C du pigeon d'argile et de la balle a donc la même valeur.

x_C = OA = 45 m

2) x_P = x_C Þ v_P0.cos a .Dt = x_C Þ Dt = x_C /(v_P0.cos a) = 45 /(30 x cos 45) = 2,1 s

3) a) On néglige toutes forces qui s'exercent sur la balle.

On applique le théorème du centre d'inertie ( 2^ème loi de Newton) à la balle dans le référentiel terrestre supposé galiléen :

m_B . a_B = 0 Þ a_B = 0

a_B = dv_B/dt = 0 Þ v_B = v_B0 La vitesse est constante.

b) v_By = v_B0 = dy_B/dt Þ y_B(t) = v_B0.t' + y_B0 = v_B0.t'

y_B(Dt') = v_B0.Dt' = y_C Þ Dt' = y_C / v_B0 = 22 / 500 = 0,044 s

4) D t est grand devant D t' , le pigeon d'argile se déplace beaucoup plus lentement que la balle.

Le tireur peut viser directement le pigeon car pendant le trajet de la balle , le pigeon d'argile aura très peu bougé.

III ) Discussion de l'effet du poids de la balle :

1) Le poids P_B force exercée par la Terre sur la balle est vertical vers le bas.

On applique le théorème du centre d'inertie ( 2^ème loi de Newton) à la balle dans le référentiel terrestre supposé galiléen :

m_B . a_B = P_B = m_B . g Þ a_B = g

a_By = a_B = - g ; a_Bx = 0 ; a_By = dv_By/dt Þ v_By(t) = - g.t ' + v_B0y = - g.t ' + v_B0

2) v_By(0,044) = - 10 x 0,044 + 500 = 499,6 m.s^-1 » 500 m.s^-1

La vitesse de la balle est presque constante sur le trajet, l'influence du poids de la balle est ici négligeable.

Afrique Juin 2004 - III ) (spe) Le microscope réel :

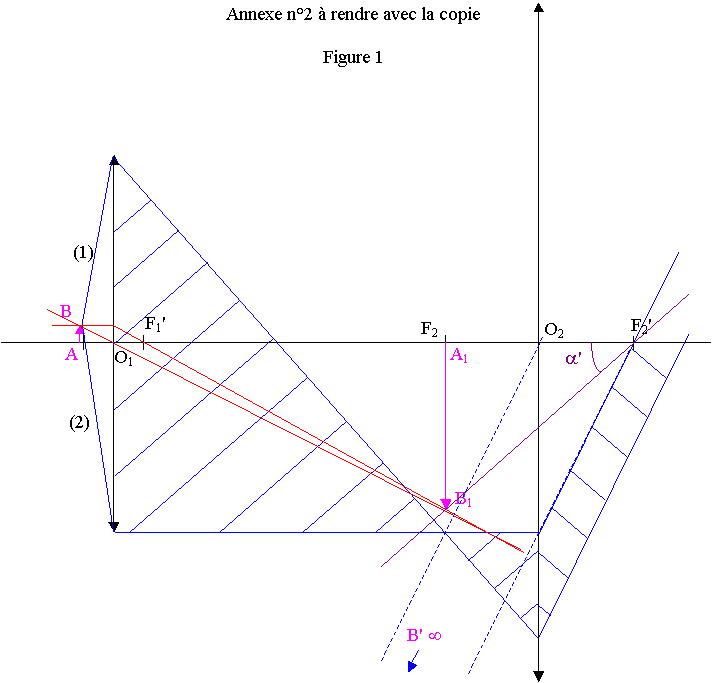
1 ) Construction de l'image définitive A'B'

1.1) Schéma

1.2) L'image intermédiaire joue le rôle d'objet pour l'oculaire.

1.3) L'image intermédiaire est dans le plan focal objet pour l'oculaire, l'image A'B' donnée par le microscope est donc à l'infini.

2) Observation d'un grain de pollen.

2.1.1) AO₁ = 17,6 mm. formule de conjugaison : 1//₁Å₁ – 1/ /₁Å = 1/f₁'

1//₁Å₁ = 1/ /₁Å + 1/f₁' Þ /₁Å₁ = 1/ (1/ /₁Å + 1/f₁' ) Þ /₁Å₁ = 1/ (- 1/17,6 + 1/16,0 ) = 176 mm

2.1.2) /₁F₂ = /₁F₁ + F₁F₂ = 16,0 + 160 = 176 mm = /₁Å₁ . A₁et F₂ sont confondus.

2.1.3) L'image A'B' est située à l'infini car l'objet A₁B₁ est dans le plan focal objet de l'oculaire.

2.1.4) g₁ = Å₁B₁ / ÅB = -10 Þ A₁B₁ = 10 x AB = 500 mm = 5,0.10^-4 m = 0,50 mm

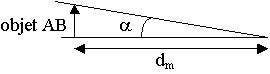2.2.1) Le diamètre apparent d'un objet est l'angle a avec lequel l'objet est vu à l'œil nu.

2.2.2) tan a = AB / d_m ; a étant petit, tan a » a ; a » 50.10^-6 / 25.10^-2 » 2,0.10^-4 rad

2.2.3) a < 3,0.10^-4 rad, ce grain de pollen n'est donc pas visible à l'oeil nu.

2.3.1) tan a' = A₁B₁ / A₁F₂' = A₁B₁ / 2 f₂'

a' étant petit, tan a' » a' ; a' » 5,0.10^-4 / 50.10^-3 » 1,0.10^-2 rad

2.3.2) G = a' / a = 1,0.10^-2 / 2,0.10^-4 = 50

3.1) Le cercle oculaire est l'image de la monture de l'objectif par l'oculaire.

3.2) voir figure 2

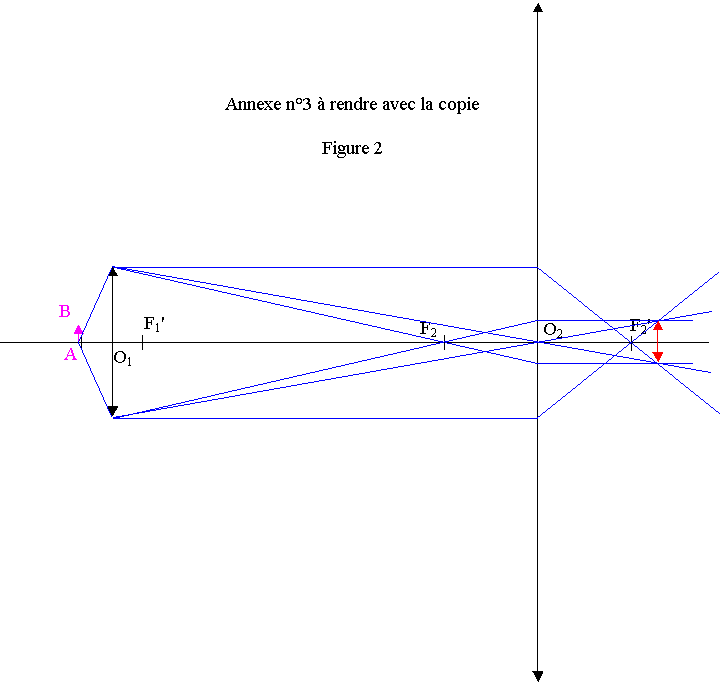
3.3) Le cercle oculaire correspond à la section la plus étroite du faisceau qui sort du microscope. C'est à cet endroit qu'il faut placer l'œil pour recevoir le maximum de lumière. Son diamètre doit être inférieur au diamètre de la pupille de l'œil.