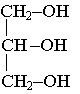Correction Bac France Juin 2004
Calculatrice autorisée
I – A propos de l'aspirine (4 points)
II - Mécanique du vol d'un ballon sonde(3 points)
III – Bizarre, bizarre (4 points)
I – L'eau de Dakin (spécialité) (4 points)
Juin 2004 - I )A propos de l'aspirine :
1) Etude de la transformation chimique par une mesure de pH :
1.1) pHS = 2,9 ; [H3O+]éq = 10 – pH = 10 – 2,9 = 1,26.10-3 mol.L-1
1.2) AH(aq) + H2O(aq) = A-(aq) + H3O+(aq)
1.3) n(AH)0 = cS.VS = 5,55.10-3 x 500,0.10-3 = 2,77.10-3 mol
|
Equation chimique |
AH(aq) + H2O(l) = A-(aq) + H3O+(aq) |
||||
|
Etat du système |
Avancement |
Quantité de matière en mol |
|||
|
Etat initial |
0 |
n(AH)0 |
excès |
0 |
0 |
|
En cours |
x |
n(AH)0 – x |
excès |
x |
x |
|
Etat final |
xf |
n(AH)0 – xf |
excès |
xf |
xf |
xf = n(H3O+)éq = [H3O+]éq . VS = 1,26.10-3 x 0,500 = 6,3.10-4 mol
1.4) Si la réaction est totale, n(AH)f = 0 = n(AH)0 – xmax Þ xmax = 2,77.10-3 mol
1.5) t = xf / xmax = 6,3.10-4 / 2,77.10-3 = 0,227 = 22,7 %
2) Détermination de la constante d'équilibre de la réaction par conductimétrie :
s = 44 mS.m-1
2.1) D'après le tableau d'avancement , [H3O+]éq = [A-]éq = xf / VS
s = (l(H3O+) + l(A-)).xf / VS Þ xf = s.VS / (l(H3O+) + l(A-))
2.2) xf = 44.10-3 x 500,0.10-6 / (35,0.10-3 + 3,6.10-3) = 5,70.10-4 mol
2.3) [AH]éq = (n(AH)0 – xf) / VS = (2,77.10-3 - 5,7.10-4) / 0,500 = 4,4.10-3 mol.L-1
[A-]éq = xf / VS = 5,70.10-4 / 0,5 = 1,14.10-3 mol.L-1
[H3O+]éq = [A-]éq = 1,14.10-3 mol.L-1
2.4) K = [H3O+]éq.[A-]éq / [AH]éq ; K = (xf / VS)2 / ((n(AH)0 – xf) / VS)
K = xf2 / ((n(AH)0 – xf).VS) = (5,70.10-4)2 / ((2,77.10-3 - 5,7.10-4) x 0,500) = 2,95.10-4
pK = 3,53 , cela correspond bien à pKA .
3) D'après le tableau , la méthode conductimétrique est plus précise car l'écart pour la méthode pH-métrique est plus grand que pour la méthode conductimétrique.
©Sciences Mont Blanc
Juin 2004 - II )Mécanique du vol d'un ballon sonde
:
1) Mécanique du vol :
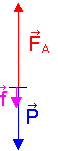
1.1.1) Il y a deux forces qui s'exercent sur le ballon : son poids P vertical vers le bas et la poussée d'Archimède exercée par l'air FA verticale vers le haut.
L'air peut aussi exercer une force verticale f vers le bas , qui peut être négligé à faible vitesse.
1.1.2) FA = mair déplacée.g = r.Vb.g
1.1.3) On applique la 2ème loi de Newton au système (ballon + nacelle) dans le référentiel terrestre supposé galiléen : FA + P + f = M.a
1.1.4) Il faut que a soit vertical vers le haut . On néglige la force de frottement f
Projection sur un axe vertical vers le haut : FA – P = M.a > 0 Þ FA > P Þ r.Vb.g > M.g
condition : M < r.Vb
1.1.5) Mmax = r.Vb =1,22 x 9,0 = 11 kg ; mmax matériel = 11 – 2,10 – 0,50 = 8,4 kg
1.2) Ascension du ballon :
1.2.1) On tient compte de la force de frottement f :
FA + P + f = M.a Þ FA – P – f = M.a Þ r.Vb.g - M.g – K.r.v2 = M.dv/dt
(r.Vb.g / M –g) – K.r.v2 / M = dv/dt Þ B + A.v2 = dv/dt
A = - K.r / M et B = g.(r.Vb / M – 1)
M = 2,0 + 2,1 + 0,50 = 4,6 kg
1.2.2) (dv/dt) = 13,6 – 0,53 v2 ; v0 = 0 m.s-1 ; a(t0) = (dv/dt)0 = 13,6 m.s-2
Dv(t0) = (dv/dt)0.Dt = 13,6 x 0,05 = 0,68 m.s-1 ; v(t1) = v(t0) + Dv(t0) = 0,68 m.s-1
a(t1) = (dv/dt)1 = 13,6 – 0,53 v(t1)2 = 13,6 – 0,53 x 0,682 = 13,3 m.s-2
Dv(t1) = (dv/dt)1.Dt = 13,3 x 0,05 = 0,668 m.s-1 ; v(t2) = v(t1) + Dv(t1) = 0,68 + 0,668 = 1,35 m.s-1
1.3) Vitesse limite du ballon :
1.3.1) Lorsque la vitesse limite est atteinte, elle est constante, dv/dt = 0 = B + A.vl2
vl = ![]() (-B/A)
(-B/A)
1.3.2) vl = ![]() (13,6 / 0,53) = 5,06 m.s-1
(13,6 / 0,53) = 5,06 m.s-1
1.3.3) D'après le graphique, la vitesse limite est un peu supérieure à 5 m.s-1 , ce qui correspond au calcul précédent.
2.1) Dg / g = ½(g9000 – g0) / g0½ = ½9,7789 – 9,8066½/ 9,8066 = 2,82.10-3 = 0,28 %
D'après le calcul précédent , pour les altitudes considérées, Dg / g < 0,28 %
On peut donc considérer g comme constante.
2.2) FA = r.Vb.g , g est constante, Vb augmente, r diminue, on ne peut donc pas conclure.
©Sciences Mont Blanc
Juin 2004 - III )Bizarre, bizarre :
1) Quand la cendre et le suif s'emmêlent :
1.1) KOH(s) = K+(aq) + HO-(aq)
|
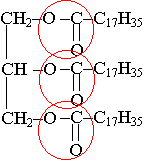
1.2.1) Le tristéarate de glycéryle appartient à la famille des triesters. Il a 3 fonctions esters |
|
|
1.2.2) formule de l'acide : C17H35 –COOH
L'alcool est le glycérol de formule : |
|
Cette réaction est une estérification.
1.3.1) Saponification :
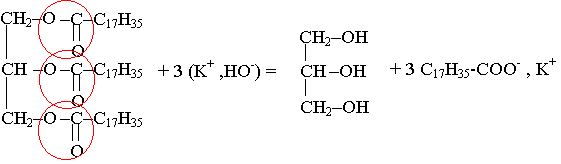 |
1.3.2) C17H35-COO- a une partie hydrophile –COO-
Une partie hydrophile est un morceau de molécule qui aime l'eau.
2) Principe de fonctionnement d'un tube fluorescent :
2.1) Dans les spectres des tubes 1 et 2, on retrouve celui de la lampe à vapeur de mercure.
Les deux tubes contiennent des vapeurs de mercure.
2.2.1) Le niveau le plus bas E0 est l'état fondamental.
2.2.2) L'atome de mercure est alors dans un état excité.
2.2.3) a) La perte d'énergie se manifeste par l'émission d'une radiation lumineuse .
b) DE = h.n = h.c / l ; DE = E1 – E0 = - 5,54 + 10,44 = 4,9 eV = 4,9 x 1,6.10-19 = 7,84.10-19 J
l1 ® 0 = h.c / DE = 6,63.10-34 x 3,00.108 / 7,84.10-19 = 2,54.10-7 m = 254 nm
c) Les longueurs d'onde du domaine visible sont comprises entre 400 nm et 800 nm.
La radiation de longueur d'onde l1 ® 0 est dans le domaine de l'U.V. car l1 ® 0 < 400 nm.
2.3.1) D'après ce qui précède, la vapeur de mercure peut émettre une radiation lumineuse de longueur d'onde comprise de 254 nm , la poudre soumis à cette radiation, va émettre de la lumière visible dont le spectre est continu.
2.3.2) Une lampe à vapeur de mercure donne une lumière dont le spectre est discontinu (figure 3) et ne donne pas un éclairage satisfaisant; en ajoutant de la poudre dans le tube, on voit d'après la figure 2, que l'on obtient en plus un spectre continu de 400 nm à 670 nm, ce qui donne cette fois un éclairage confortable proche de la lumière blanche.
2.3.3) En observant la figure 2, on constate que le spectre est continu et d'intensité presque constante, le tube 2 donne une lumière proche de la lumière blanche. La figure 1 montre au contraire que les radiations les plus intenses sont comprises entre 550 et 650 nm, le tube 1 donne donc une lumière colorée. En choisissant bien la poudre, on peut obtenir des éclairages de différentes couleurs.
©Sciences Mont Blanc
Juin 2004 - I )L'eau de Dakin (spécialité)
:
1) Dosage par
spectrophotométrie du permanganate de potassium en solution :
1.1) M(KMnO4)
= MK + MM + 4 x MO = 39,0 + 55,0 + 4 x 16,0
= 158 g.mol-1
m(KMnO4) = C0.V0.M = 1,0.10-2 x 0,500 x 158 = 0,79 g
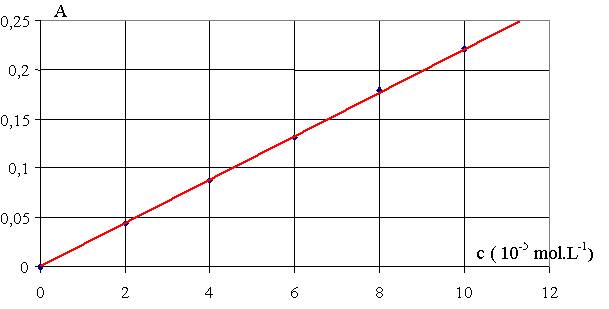 |
1.2.1) Si c = 0 mol.L-1 A
= 0
D'après le graphique, la courbe est une droite passant par l'origine. A = k . c k : constante
k est coefficient directeur de la droite.
Pour déterminer k, on prend 2 points, l'origine O ( 0, 0 ) et le point M (10.10-5 , 0,221)
k = (0,221 – 0) / (10.10-5 – 0) = 2210 L.mol-1
1.2.2) On mesure l'absorbance A à la longueur d'onde 530 nm.
On choisit la longueur d'onde de façon à ce que l'espèce étudiée absorbe beaucoup à cette longueur d'onde. D'après la figure 1, la longueur d'onde choisie , correspond à un maximum d'absorption.
1.2.3) Le spectre présente des absorptions allant jusqu'à 2,5 alors que précédemment A ne dépasse pas 0,221. On a donc utilisé une solution plus concentrée pour obtenir le spectre de la figure 1.
1.3.1) A = 0,14 . D'après le graphique, cexp = 6,4.10-5 mol.L-1 .
1.3.2) m(KMnO4 ) = 0,0010 g V = 100 mL
c = n / V = (m / M) / V = (0,0010 / 158) / 0,10 = 6,33.10-5 mol.L-1
Ce résultat est tout à fait compatible avec ce qui précède.
½( c – cexp ) / c ½ = ½(6,33.10-5 – 6,4.10-5) / 6,33.10-5 ½= 0,011 = 1,1 %
2) Détermination de la masse de chlore actif
2.1) Cl2 (g) + 2 e- = 2 Cl-(aq) et 2 ClO-(aq) + 4 H+(aq) + 2 e- = Cl2 (g) + 2 H2O(l)
2.2.1) V = 0,1 L ; V(Cl2) = 170 mL = 0,170 L
On utilise de l'eau salée pour éviter que le gaz dichlore ne se solubilise dans l'eau salée car il y est très peu soluble.
2.2.2) n(Cl2) = V(Cl2) / VM = 0,170 / 24,0 = 7,08.10-3 mol
m(Cl2) = n(Cl2).M(Cl2) = 7,08.10-3 x (35,5 x 2) = 0,496 g
m = 0,5 g ; ½(m – mexp) / m ½= ½(0,5 – 0,496) / 0,5½= 8,3.10-3 = 0,83 %
3) Il faut maintenir l'eau de Dakin basique pour éviter la réaction (1) qui dégage du dichlore qui est toxique.
©Sciences Mont Blanc