Correction Bac

Calculatrice autorisée

Liban Juin 2004 - I ) Chimie et spéléologie :

V_S = 100 mL = 0,10 L ; Ca = 0,1 mol.L^-1 ; m(CaCO₃) = 2,0 g

1) d = M / 29 ; M(CO₂) = M_C + 2 M_O = 12 + 2 x 16 = 44 g.mol^-1

d_CO2 = M_CO2 / 29 = 44 / 29 = 1,52

Le dioxyde de carbone CO₂ est plus dense que l'air (d_CO2 > 1 ) , il s'accumule donc au voisinage du sol, dans les parties inférieures de la grotte.

2) n(H₃O⁺)₀= Ca.V_S= 0,10 x 0,10 = 1,0.10^–2 mol ; M(CaCO₃) = M_Ca+ M_C+ 3 M_O= 100 g.mol^-1

n(CaCO₃) = m / M = 2,0 / 100 = 2,0.10^–2 mol

équation chimique		CaCO₃ _(s) + 2 H₃O⁺_(aq) = Ca²⁺_(aq) + CO₂ _(g) + 3 H₂O_(l)
état du système	Avancement (mol)	Quantités de matière (mol)
état initial	0	2,0.10^–2	1.10^–2	0	0	excès
en cours	x	2,0.10^–2 – x	1.10^–2 – 2 x	x	x	excès
état final	x_f	2,0.10^–2 – x_f	1.10^–2 – 2 x_f	x_f	x_f	excès

Si CaCO₃ est le réactif limitant alors n(CaCO₃)_f = 0 = 2,0.10^–2 – x_max Þ x_max = 2,0.10^–2 mol

Si H₃O⁺ est le réactif limitant alors n(H₃O⁺)_f = 0 = 1.10^–2 – 2x_max Þ x_max = 5,0.10^–3 mol

Le réactif limitant est l’ion oxonium H₃O⁺ ( il conduit à l’avancement maximal le plus faible)

x_max = 5.10^–3 mol

4) a) D’après l’équation chimique , CO₂ est le seul gaz formé, et n(CO₂) = x

D’après la loi des gaz parfaits : P(CO₂) .V(CO₂) = n(CO₂).R.T avec P en Pa, V en m³, et T en °K.

P(CO₂) = P_atm ; V(CO₂) = 0,10 L = 1,0.10^-4 m³ ; T = 298°K

P_atm.V(CO₂) = x . R . T Þ x = P_atm.V(CO₂) / (R.T)

à la date t = 20 s, V(CO₂) = 29 mL = 2,9.10^–5 m³

x = 1,020.10⁵ x 2,9.10^-5 / ( 8,31 x 298 ) = 1,2.10^–3 mol

b) Si la réaction est totale , x = x_max = 5.10^-3 mol

V(CO₂)_max = n(CO₂)_max.R.T / P_atm = 5.10^-3 x 8,31 x 298 / 1,020.10⁵ = 1,21.10^-4 m³ = 121 mL

D'après le tableau de valeurs de V(CO₂ ) , V(CO₂)_f = V(CO₂ )_max

La transformation est donc totale mais lente.

5)a) v = (1 / V_S).dx/dt

D'après le graphique x = f(t), au début x augmente vite, dx/dt est grand, la vitesse v est grande ( on peut visualiser cela en traçant la tangente à la courbe). Au cours du temps, x augmente moins vite jusqu'à atteindre x_max, dx/dt diminue jusqu'à s'annuler.

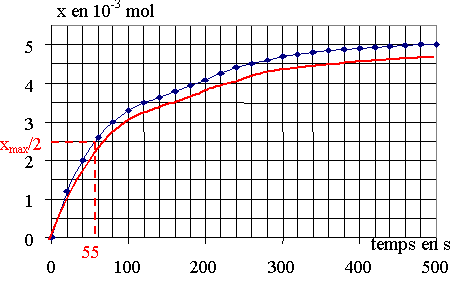
b) Le temps de demi-réaction t_1/2 est la durée au bout de laquelle l'avancement x vaut x_max/2.

D'après le graphique, t_1/2 » 55s

6) a) La température est un facteur cinétique pour une réaction lente, si on diminue la température, la vitesse de réaction diminue mais l'état final n'est pas modifié.

b) L'allure de l'évolution de l'avancement à une température est tracé en rouge sur le graphique.

7) a) Les ions présents dans la solution sont les ions oxonium H₃O⁺ , les ions calcium Ca²⁺ et des ions chlorure Cl^- . L'ion Cl^- ne réagit pas , il est spectateur, sa concentration ne change pas

b) La conductivité ionique molaire des ions H₃O⁺ est plus grande que celle des ions Ca²⁺ .

Globalement, 2 ions H₃O⁺ sont consommés et 1 ion Ca²⁺ est formé.

La conductivité de la solution diminue donc.

c) s(0) = l(H₃O⁺ ).[H₃O⁺]₀ + l(Cl^-).[Cl^-]₀ = (l(H₃O⁺) + l(Cl^- )).Ca ( Ca en mol.m^-3 )

s(0) = (35,0 + 7,5).10^-3 x 0,1.10³ = 4,25 S.m^-1

d) s = l(H₃O⁺ ).[H₃O⁺] + l(Cl^-).[Cl^-] + l(Ca²⁺).[Ca²⁺]

s = l(H₃O⁺ ).( Ca – 2x / V_S ) + l(Cl^-).Ca + l(Ca²⁺).x / V_S ( V_S en m³ )

s = (l(H₃O⁺) + l(Cl^- )).Ca + x.( l(Ca²⁺) – 2 l(H₃O⁺ )) / V_S

s = 4,25 + x ( 12,0.10^-3 – 2 x 35,0.10^-3 ) / 0,1.10^-3 = 4,25 – 580 x

e) s (x_max) = 4,25 – 580 x 5.10^-3 = 1,35 S.m^-1

©Sciences Mont Blanc

II ) Enquête sur un homocide :

I ) Etude du carbone 14 :

Dans la nature le carbone existe sous forme de deux noyaux isotopes et

Dans la haute atmosphère, un neutron formé par l'action de rayons cosmiques bombarde un noyau d'azote 14 () qui se transforme en carbone 14 () radioactif b^- avec émission d'une autre particule.

1) + ®+

La particule émise est un proton .

Pour obtenir l'équation, on applique les règles de Soddy : conservation du nombre de charge et conservation du nombre de masse.

2) ®+

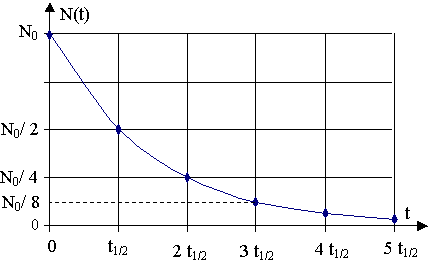
3) Le temps de demi-vie t_1/2 est la durée au bout de laquelle la moitié des noyaux d'un échantillon a été désintégré.

4) a) N(t½) = N₀ / 2 ;
N(2t½) = N(t½) / 2 = N₀ / 4 ;
N(3t½) = N(2t½) / 2 = N₀ / 8 ;

N(4t½) = N(3t½) / 2 = N₀ / 16 ;
N(5t½) = N(4t½) / 2 = N₀ / 32

b) graphique ci-dessus

5) a) N(t_1/2) = N₀ / 2 = N₀.e^-^l^.t Þ ln ½ = - l.t_1/2 Þ t_1/2 = ln 2 / l

b) l = ln 2 / t_1/2 = ln 2 / 5570 = 1,24 an^-1; l = ln 2 / (5570 x 365,25 x 24 x 60 x 60) = 3,94.10^-12 s^-1

II ) Application à la datation :

1) A(t) = - dN(t)/dt = l.N(t) Þ l.N(t) + dN(t)/dt = 0 (2)

b) N(t) = N₀.e^-^l^.t ; dN(t)/dt = - l.N₀.e^-^l^.t

(2) l.N(t) + dN(t)/dt = l.N₀.e^-^l^.t - l.N₀.e^-^l^.t = 0

L'expression de N(t) donnée par la relation (1) est solution de cette équation différentielle.

2) a) N /N₀ = 1,64.10^-2 = e^-^l^.t Þ t = - ln(N / N₀) / l = - ln (1,64.10^-2) / 1,24.10^-4 = 3,30.10⁴ ans

( pour SAPIAND : t = - ln(N / N₀) / l = - ln (1,87.10^-2) / 1,24.10^-4 = 3,20.10⁴ ans )

b) L'âge calculé pour les ossements ANDER correspond aux données fournies par l'agence de presse, il est entre 30 000 et 60 000 ans.

c) N_ANDER / N₀ < N_SAPIAND / N₀ Þ Ils n'ont pas vécu à la même époque, SAPIAND a vécu nettement après ANDER. SAPIAND n'a pas pu massacrer ANDER.

3) a) 1 Becquerel correspond à une désintégration par seconde.

A(200 g d'os) = 15 desint. / min = 15 / 60 = 0,25 Bq

b) A₀ = l.N₀ Þ N₀ = A₀ / l = 0,25 / 3,94.10^-12 = 6,34.10¹⁰ noyaux

c) N_C = N_A.n_C = N_A.m_C / M_C = 6,02.10²³ x 1 / 12 = 5,02.10²² atomes

N() = N_C et N() = N₀
Þ N() / N() = 6,34.10¹⁰ / 5,02.10²² = 1,26.10^-12

©Sciences Mont Blanc

Liban Juin 2004 - III ) Le grand saut :

Partie A :

P = m.g = 1,6.10³ x 9,8 = 1,57.10⁴ N

P_A = m_air.g = m_air.V_b.g = 1234.10^-3 x 4,0.10³ x 9,8 = 4,84.10⁴ N

P_A > P ; grâce à la poussée d'Archimède de l'air, le ballon peut s'élever facilement du sol.

Partie B :

1) Dans la première partie du saut, la vitesse est assez faible. D'après la pression de l'air et sa masse volumique, la quantité d'air est faible, les frottements de l'air sont donc faibles, d'autant qu'à ce stade du saut, le corps du parachutiste est aérodynamique.

On peut donc négliger l'action de l'air sur le parachutiste, il n'est donc soumis qu'à son poids, il est donc en chute libre.

2) On étudie le système ( parachutisme + équipement) dans le référentiel terrestre galiléen auquel on associe un repère (O, i ) ( i vecteur normé vertical vers le bas et O , point de départ du saut )
On applique la 2^ème loi de Newton : S F _ext = m.a Þ P = m.a Þ g = a Þ g.i = a.i Þ a = g

a = dv /dt = g Þ v = g.t + k ( k constante) ; à t = 0 s, v = k = v₀ = 0 Þ v = g.t

v = dx / dt = g.t Þ x = ½ g.t² + k' ( k' constante) ; à t = 0 s , x = k' = 0 Þ x = ½ g.t²

a) t₁ = v_son / g = ( 1067.10³ / 3600 ) / 9,7 » 30,6 s. Cela correspond à la valeur de l'énoncé.

b) x₁ = ½ g.t₁² = ½ 9,7 x 30,6 ² » 4 530 m. h₁ = h – x₁ = 40 000 – 4530 » 35 500 m

c) Ces valeurs correspondent à peu près à celles indiquées dans le document p9.

Partie C : Chute dans la basse atmosphère (troposphère) :

1) k = F /v² ; [F] = [m.a] = M.(L.T^-2)

[k] = [F] / [v]² = [m.a] / [v]² = M.( L.T^-2) / (L.T^-1)² = M.L^-1 ; k se mesure en kg.m^-1

2) Dans les conditions citées, on peut négliger la poussée d'Archimède de l'air raréfié.

Les forces s'exerçant sur le système sont : son poids P et la force de frottement de l'air f .

On étudie le système ( parachutisme + équipement) dans le référentiel terrestre galiléen auquel on associe un repère (O, i ) ( i vecteur normé vertical vers le bas et O , point de départ du saut )

On applique la 2^ème loi de Newton : S F _ext = m.a Þ P + f = m.a Þ m.g.i - k.v².i = a.i

Þ a = dv / dt = g – (k / m).v² Þ dv / dt = g – (k / m).v²

3) a) La méthode d'Euler consiste à assimiler l'accélération a = dv/dt à Dv/Dt sur un intervalle de temps Dt très court. Dv = a_n .Dt Þ v_n+1 = v_n + a_n .Dt ; a_n = g - (k / m).v_n²

v_n+1 = v_n + (g - (k / m).v_n².Dt = v_n + g.Dt – (k.Dt / m).v_n² = v_n + A – B.v_n²

A = g.Dt = 9,8 x 0,5 = 4,9 et B = k.Dt / m = 0,78 x 0,5 / 200 = 1,95.10^-3

[A] = [v_n] , A a donc la dimension d'une vitesse et se mesure en m.s^-1

[v_n+1] = [B].[v_n]² Þ [B] = [v] / [v]² = 1 / [v] = T.L^-1 . B se mesure en s.m^-1

b) D'après le graphe (figure 1), il faut environ 10s pour atteindre la vitesse limite et

v_limite = 50 m.s^-1 = 180 km.h^-1

Cette valeur correspond à celle indiquée sur le film.

Remarque : Ce sujet sur le grand saut est déjà déjà tombé dans le sujet bac Pondichéry Avril 2004

Liban Juin 2004 - III ) Emission et réception radio (spe):

A ) Emission

1) Une telle onde modulée est caractérisée, au cours du temps, par une amplitude variable, dont les variations dépendent du signal à transmettre, et une fréquence constante.

2) La fréquence de la porteuse doit être très supérieure à la fréquence du son à transmettre.

3) Un son audible a une fréquence comprise entre 20 Hz et 20 kHz.

B ) Réception :

1) Etude de la partie 1 du circuit :

a) La partie 1 est constitué d'une antenne et d'un filtre passe-bande LC .

L'antenne capte les ondes électromagnétiques et le filtre ne laisse passer qu'une bande étroite de fréquences. On peut ainsi choisir la bande de fréquences correspondante à une station radio

b) Le filtre LC laisse passer avec un maximum d'amplitude, la tension dont la fréquence correspond à la fréquence propre f₀ des oscillations électriques dans le circuit LC.

f₀ = 1/ [2p (L.C)] Þ C = 1/ [ L.(2pf₀)²]

C_min = 1/ [1,0.10^-3 x (2 x 3,14 x 10.10³)²] = 2,5.10^-7 F = 0,25 mF

C_max = 1/ [1,0.10^-3 x (2 x 3,14 x 1,0.10³)²] = 2,5.10^-5 F = 25 mF

Il faut donc que la capacité C soit compris entre 0,25 mF et 25 mF.

2) Etude des parties 2 et 3 du circuit :

a) La partie 2 est un détecteur d'enveloppe qui démodule la tension.

La partie 3 est un filtre passe-haut qui élimine la composante continue de la tension démodulée.

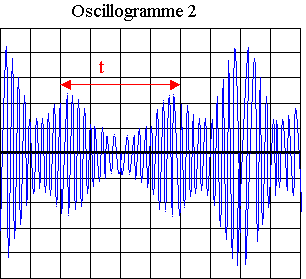
b) La tension u_AM est la tension modulée, celle de l'oscillogramme 2.

La tension u_BM est la tension démodulée contenant une composante continue, celle de l'oscillogramme 3.

La tension u_SM est la tension correspondant au signal transmis, celle de l'oscillogramme 1.

c) Le seul oscillogramme où la porteuse est visible est l'oscillogramme 2.

Sur le temps t fléché sur l'oscillogramme 2, il y a 20 périodes T. 20 T = 4 x 1 = 4 ms ;

T = 0,2 ms ; f = 1 / T = 1 / 0,2.10^-3 = 5 000 Hz = 5,0 kHz

C ) Analyse du son reçu

1) La hauteur du son est caractérisée par sa fréquence f.

D'après le graphe, la période T_S du son vaut 0,0080 s, soit 8,0 ms. f = 1 / T = 1 / 8.10^-3 = 125 Hz

2) Les fréquences qui apparaissent sur ce spectre sont celles du mode fondamental f₀ = 125 Hz et celles des harmoniques dont la valeur est multiple de f₀, 250 Hz, 375 Hz et 500 Hz.

3) La fréquence du mode fondamental qui est aussi celle du son, est la même que celle du son précédent. La hauteur est donc la même.

Par contre, il y a plus d'harmoniques et les amplitudes des différents modes sont différentes pour le 2^ème son. Le timbre de ces sons est donc différent.