Correction Bac Nouvelle Calédonie Novembre 2004

Calculatrice autorisée

 

I ) Deux isotopes de l'iode pour étudier la thyroïde (4 points)

II ) Etat final d'un système chimique : étude par spectrophotométrie (6,5 points)

III ) Le lancer du poids au championnats du monde 2003 (5,5 points)
I ) (spe) (4 points)

 

Nouvelle Calédonie Novembre 2004 - I ) Deux isotopes de l'iode pour étudier la thyroïde :

1) Le noyau de l'isotope ¹³¹₅₃I contient 53 protons (Z) et 78 neutrons ( A – Z = 131 – 53 = 78)

2) N₀ = n . N_A = (m / M) . N_A = (1,00.10^-6 / 131) x 6,02 10²³ = 4,60.10¹⁵ atomes.

3) Il y a conservation du nombre global de nucléons et du nombre global de charge

¹³¹₅₃I    est radioactif b^-., il se désintègre en émettant un électron  ⁰_-1 e

¹³¹₅₃I ® ⁰_-1 e + ^A_Z X           131 = A + 0  ;  A = 131  ;   53 = -1 + Z  ;  Z = 54

Le noyau produit est donc  ¹³¹₅₄ Xe .     équation :  ¹³¹₅₃I ® ⁰_-1 e + ¹³¹₅₄ Xe           

4.1) loi de décroissance radioactive  :  N(t) = N₀ . e^{- l . t}

4.2.1) La demi-vie t_½ d'un échantillon radioactif est le temps au bout duquel la moitié de la quantité initiale de noyaux a été désintégrée. N(t + t_1/2) = N(t) / 2.

4.2.2) N(t_1/2) = N₀ / 2     ;   N₀. e ^{- l . t1/2} = N₀ / 2   ;   ln(e ^{- l . t1/2} ) = ln(1/2)  ;

 - l . t_1/2 = - ln 2      ;      ln 2 = l . t_½.

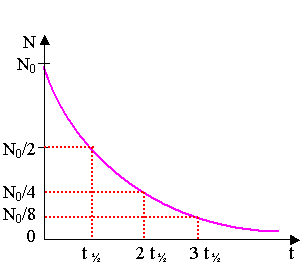
4.3) N(t_1/2) = N₀ / 2     ;  

N(2t_1/2) = N(t_1/2) / 2 = N₀ / 4  ; 

N(3t_1/2) = N(2t_1/2) / 2 = N₀ / 8

5.1) N(t) = N₀ . e^{- l . t}   ;    dN(t)/dt = - l . N(t)    ;   A(t) = l . N(t)

5.2) A₀ = l . N₀ = N₀ . ln 2 / t_1/2        ;     t_1/2 = 8 x 24 x 60 x 60 = 6,91.10⁵ s

A₀ = 4,60.10¹⁵ x ln 2 / 6,91.10⁵ = 4,61.10⁹ Bq

5.3) A_4h = A₀ . e ^{- l . t} = 4,61.10⁹ x exp ( - (ln 2 / 6,91.10⁵) x (4 x 60 x 60)) = 4,54.10⁹ Bq

5.4) |DA|/A₀ = |A(t)-A₀| / A₀ = (4,61.10⁹ - 4,54.10⁹) / 4,61.10⁹ = 0,015 = 1,5 %

6) t_1/2(¹²³I) = 13,2 h = 4,75.10⁴ s.

A₀ = 4,61.10⁹ Bq   ;    A / A₀ = e ^{- l' . t}   ;  t = ( ln(A₀ / A) ) / l' = ( ln(A₀ / A) ) . t_1/2 / ln 2

t = (ln (4,61.10⁹ / 4,54.10⁹)) . 4,75.10⁴ / ln 2 = 1048 s = 17 min 28s

Cette durée est donc plus courte que celle obtenue avec de l'isotope ¹³¹₅₃I.

 

©Sciences Mont Blanc

 

 

 

Nouvelle Calédonie Novembre 2004 - II ) Etat final d'un système chimique : étude par spectrophotométrie :

I ) Suivi spectrophotométrique de la transformation chimique.

1) On peut suivre la cinétique d'une réaction par pH-métrie si la réaction implique des ions H₃O⁺ ou HO^- , ou par conductimétrie si la réaction le permet, ou par mesure de pression d'un gaz

 

2) a) A = k . c  ;   k = A / c = 1,70 / 5,0.10^-3 = 3,4.10² L.mol^-1 

 

b) A(t) = k . [I₂] = k . n(I₂)(t) / (V₁+V₂)   ;  n(I₂)(t) = A(t).(V₁+V₂) / k 

 

c) n(I₂)(90) = 0,79 x (10,0 + 10,0).10^-3 / 3,4.10² = 4,6.10^-5 mol

 

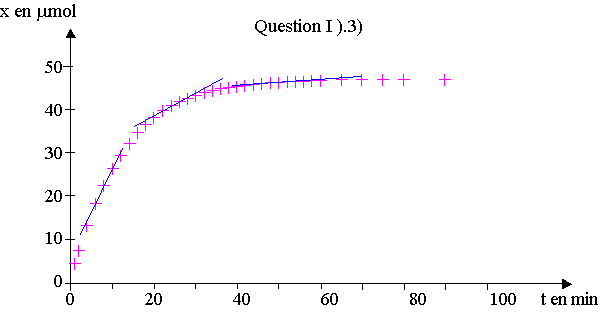
3) a) dx/dt correspond au coefficient directeur de la tangente à la courbe.

En traçant la tangente à différents points de la courbe , on constate que le coefficient diminue au cours du temps, la vitesse volumique diminue au cours du temps.

 

b) Au cours du temps, les concentrations des réactifs diminuent, or c'est un facteur cinétique, cela diminue la vitesse de réaction.

c) Pour accélérer la réaction, on peut chauffer le mélange réactionnel, ou ajouter un catalyseur de la réaction. Cela ne modifie pas le mélange final.

 

II ) titrage du diiode formé après 90 minutes de réaction.

 

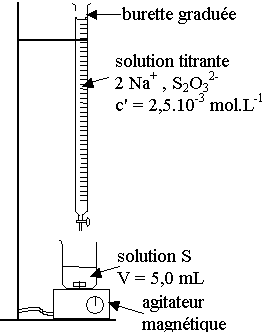
1) schéma du dispositif de titrage :

 

2) A l'équivalence, les réactifs ont été mélangés dans les proportions stœchiométriques de l'équation : 

n(S₂O₃^2-)_versé = 2 n(I₂)₀

 

3) Exploitation du titrage.

a) n(I₂)₀ = n(S₂O₃^2-)_versé / 2 = c' . V'_E / 2     (quantité dans un volume de 5 mL)

On cherche la quantité de I₂ dans les 20 mL de solution, il faut donc multiplier par 4.   

n(I₂)₉₀ = 2 c' . V'_E

 

b) n(I₂)₉₀ = 2 x 2,5.10^-3 x 9,2.10^-3 = 4,6.10^-5 mol

c) Cette valeur est la même que celle trouvée au I )2) .

III ) Etude théorique et bilan comparatif.

1)  2 I^-_(aq) = I_{2 (aq)} + 2 e^-     et    S₂O₈^2-_(aq) + 2 e^- =  + 2 SO₄^2-_(aq)  .

On les ajoute pour obtenir :         2 I^-_(aq) + S₂O₈^2-_(aq)  = I_{2 (aq)} + 2 SO₄^2-_(aq)  

2) a) n(I^-)₀ = c₁ . V₁ = 5,0.10^-1 x 10,0.10^-3 = 5,0.10^-3 mol   

n(S₂O₃^2-_(aq))₀ = c₂ . V₂ = 5,0.10^-3 x 10,0.10^-3 = 5,0.10^-5 mol   

Relation stœchiométrique		2 I-(aq)     +     S2O82–(aq)  =   I2 (aq)  +  2SO42–(aq)
Etat du système	Avancement	Quantité de matière en mol
Etat initial	0	5,0.10-3	5,0.10-5	0,0	0,0
Au cours de la transformation	x	5,0.10-3 – 2x	5,0.10-5 - x	x	2 x
Etat final attendu	xmax	5,0.10-3 - 2xmax	5,0.10-3 - xmax	xmax	2 xmax

b) Si I^- est le réactif limitant, n(I^-)_f = 0 = 5,0.10^-3 - 2x_max  ;  x_max = 5,0.10^-3 / 2 = 2,5.10^-3 mol

Si S₂O₃^2- est le réactif limitant, n(S₂O₃^2-)_f = 0 = 5,0.10^-5 - x_max  ;  x_max = 5,0.10^-5  mol

Le réactif limitant est donc S₂O₃^2-   et x_max = 5,0.10^-5  mol

D'après le tableau, n(I₂)_f = x_max = 5,0.10^-5 mol

3) Par spectrophotométrie, on trouve n(I₂) = 4,6.10^-5 mol.

Par dosage, on trouve la même valeur pour n(I₂).

D'après la question précédente, n(I₂)_th = 5,0.10^-5 mol

½_exp(I₂) – n_th(I₂) ½/ n_th(I₂) = ½4,6.10^-5 – 5,0.10^-5½/ 5,0.10^-5 = 0,080 = 8,0 %

Ce faible écart peut s'expliquer par des erreurs expérimentales de mesures.

 

         

©Sciences Mont Blanc

 

 

 

Nouvelle Calédonie Novembre 2004 - III ) Le lancer du poids aux championnats du monde 2003 :

1 ) Etude des résultats de la simulation :

1.1) D'après la figure 1, v_0x = 10 m.s^-1 ;   v_x est constante, le mouvement sur l'axe Ox est donc uniforme  ;   v_Sx = v _0x = 10 m.s^-1 

 

1.2) D'après la figure 2, v_0y = 9,5 m.s^-1 

v₀ = (v_0x² + v_0y²) = (10² + 9,5²) = 13,8 m.s^-1 

tan a = v_0y / v_0x = 9,5 / 10 = 0,95   ;  a = 43,5°

Les différences de résultats s'explique par le manque de précision du graphique.

 

1.3) Etude du vecteur vitesse du centre d'inertie du boulet.

Au sommet de la trajectoire, le vecteur vitesse est horizontal vers la droite sinon le boulet continue à monter. 

v_Sx = 10 m.s^-1  ; v_Sy = 0 m.s^-1   ;  v_S = v_Sx = 10 m.s^-1 

 

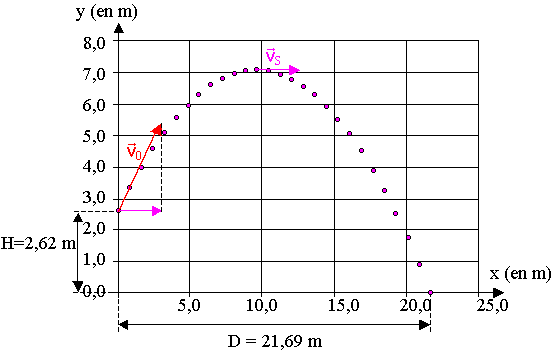
Pour être cohérent, il faut que la projection de v₀ sur Ox (v_0x) soit de même longueur que v_S.

2) Etude théorique du mouvement du centre d'inertie.

2.1) P_A = m_{air déplacé} . g = m'.V.g    ;  P = m_boulet . g = m .V.g

P_A / P = (m'.V.g ) / (m.V.g ) = m' / m = 1,29 / 7,10.10³ = 1,82.10^-4

P_A est donc négligeable devant P.

 

2.2) Les forces exercées par l'air sont négligeables, le poids est donc la seule force exercée sur le boulet, force verticale vers le bas.

On applique la 2^ème loi de Newton, dans le référentiel terrestre supposé galiléen :

P  = m . a    ;   a = g

 

2.3) Projection sur l'axe Ox :    a_x = g_x = 0 = dv_x /dt

On intègre selon la variable t  :    v_x= constante = v_0x = v₀ . cos a = dx/dt

On intègre selon la variable t  :    x = v₀ . cos a . t + constante

A t = 0s, x = constante = x₀ = 0.   x = v₀ . cos a . t

Projection sur l'axe Oy :    a_y = g_y = - g = dv_y /dt

On intègre selon la variable t  :    v_y= - g . t + constante

A t = 0s, v_y = constante = v_0y = v₀ . sin a .           v_y = - g . t + v₀ . sin a = dy/dt

On intègre selon la variable t  :    y = - ½ g . t² + v₀ . sin a . t + constante

A t = 0s, y = constante = y₀ = h.     y = - ½ g . t² + v₀ . sin a . t + h

 

2.4) t = x / (v₀.cos a).  On remplace dans l'autre équation.

y = - ½ g . x² /(v₀ .cos a)² + tan a . x + h

3 ) Comment améliorer la performance du lanceur ?

3.1)

angle a fixé	vitesse initiale v0 fixée
Quand v0 augmente, la distance horizontale D du jet  augmente	Quand a augmente, la distance horizontale D du jet augmente, passe par un maximum puis   diminue

 

3.2) Parmi les combinaisons proposées, on peut battre le record du monde avec a = 41° et

v₀ = 14 m.s^-1 puisque la vitesse v₀ est supérieure à 13,8 m.s^-1  la distance D est plus grande que 21,69 m (cas de la figure 4).

 

©Sciences Mont Blanc

 

 

Nouvelle Calédonie Novembre 2004 - I ) (spécialité) :

 

 

 

©Sciences Mont Blanc