Correction Bac Polynésie Septembre 2004

Calculatrice autorisée

 

I ) Voyager en se repérant : le GPS et les horloges (satellites - ondes) (9,5 points)

II ) Oxydo-réduction (2,5 points)

III ) Estérification (4 points)

III ) Titre alcalimétrique d'une eau minérale (4 points)

 

Correction Polynésie Septembre 2004 - I ) Voyager en se repérant : le GPS et les horloges : (satellites)

I ) Les satellites :

1) Dans le référentiel géocentrique supposé galiléen, on applique la deuxième loi de Newton au satellite  :   

      m ._G = _T®Sat.   (1)

On utilise le repère de Frenet :  soit u vecteur unitaire normal à la trajectoire et vecteur unitaire tangent à la trajectoire.

_G = _N + _T = a_N._N + a_T._T   ;   a_N = v² / d  et  a_T = dv/dt

_T®Sat = F_T®Sat ._N .    D'après la relation (1) , on a  :  

m.v² / (R_T+h)= G.m.M_T / (R_T+h)²   (2)  et   m.dv/dt = 0   (3)

On a donc dv/dt = 0, la vitesse est donc constante, le mouvement est donc circulaire et uniforme.

2) D'après la relation (2), v = (G.M_T/ (R_T+h))

3) v = (6,67.10^-11 x 5,98.10²⁴ / (6380.10³+20180.10³)) = 3 875 m.s^-1 = 13 950 km.h^-1  

v = D / T = 2 π r / T 

T = 2 π r / v = 2 x 3,14 x (6380.10³+20180.10³) / 3875 = 4,30.10⁴ s = 12 h

Cela correspond aux données de l'énoncé.

4) Ces satellites ne sont pas géostationnaires car un tel satellite a une période de 24 h.

©Sciences Mont Blanc

 

 

Correction Polynésie Septembre 2004 - I ) Voyager en se repérant : le GPS et les horloges : (ondes)

 

©Sciences Mont Blanc

 

Correction Polynésie Septembre 2004 - II )Oxydo-réduction :

Partie 1 : Oxydation directe d’un métal.

1) équation :  Cu²⁺_(aq) + Zn_(s) = Cu_(s) + Zn²⁺_(aq)

2) Q _{r, i} = [Zn ²⁺] _i / [Cu²⁺] _i = (n(Zn ²⁺) _i /V_T)/ (n(Cu²⁺) _i/V_T) = n(Zn ²⁺) _i / n(Cu²⁺) _i = c₁.V₁ / c₂.V₂

Q_{r, i} = ( 0,20 x 20.10^-3 ) / ( 0,20 x 20.10^-3 ) = 1

3) Cu²⁺_(aq)  +  Zn_(s)  =  Cu_(s)  +  Zn²⁺_(aq)   K = 10³⁷ = Q_{r, eq}

D'après le critère d'évolution spontanée, Q_{r, i} < K, le système chimique évolue dans le sens direct de l'équation, dans le sens de la formation de Cu_(s) et Zn²⁺_(aq) et de la disparition de Cu²⁺_(aq) et Zn_(s)

K > 10⁴ , on peut donc considérer la réaction quasi totale.

Cela correspond aux observations, décoloration de la solution initialement bleue et formation de métal cuivre sur la lame de zinc.

Partie 2 : Application aux piles

1) Le pont salin sert à fermer le circuit pour que le courant circule et à assurer l'électroneutralité des solutions en apportant les ions nécessaires.

2) Cu²⁺_(aq)  +  Zn_(s)  =  Cu_(s)  +  Zn²⁺_(aq)   K = 10³⁷ = Q_{r, eq}

Q _{r, i} = [Zn ²⁺] _i / [Cu²⁺] _i = 0,20 / 0,20 = 1.

D'après le critère d'évolution spontanée, Q_{r, i} < K, le système chimique évolue dans le sens direct de l'équation, dans le sens de la formation de Cu_(s) et Zn²⁺_(aq) et de la disparition de Cu²⁺_(aq) et Zn_(s)

L'électrode de cuivre donne des électrons aux ions Cu²⁺ pour former du métal Cu . Il s'agit donc de la borne positive de la pile. L'électrode de zinc est donc la borne négative de la pile.

3) A l'électrode de cuivre :  Cu²⁺_(aq) + 2 e^- = Cu_(s)

A l'électrode de zinc : Zn_(s) = Zn ²⁺_(aq) + 2 e^-

Bilan :  Cu²⁺_(aq)  +  Zn_(s)  =  Cu_(s)  +  Zn²⁺_(aq)  

4) La représentation formelle de la pile est :  ^!  Zn_(s) / Zn ²⁺_(aq) // Cu²⁺_(aq) / Cu_(s)  ^Å  

Le courant circule dans le circuit extérieur de la borne + de la pile vers la borne – de la pile.

5) Pour que la pile fonctionne, il faut que le système chimique évolue, il doit être hors équilibre. Lorsqu'il a atteint l'équilibre, il n'évolue plus et la pile est usée.

©Sciences Mont Blanc

 

 

 

Correction Polynésie Septembre 2004 - III ) Estérification :

 

Partie 1 :

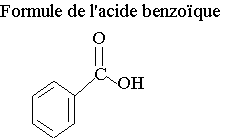
1) L'alcool A donne son nom à la 2^ème partie du nom

de l'ester méthyle. Il s'agit donc du méthanol.

 

2) C₆H₅–COOH  + CH₃–OH = C₆H₅–COO–CH₃ + H₂O

 

Partie 2 :

1)

Equation chimique		C6H5–COOH+ CH3–OH = C6H5–COO–CH3 +  H2O
Etat du système	Avancement	Quantité de matière en mol
Etat initial	0	0,20	0,20	0,0	0,0
En cours de transformation	x	0,20 – x	0,20 – x	x	x
Etat final	xéq	0,20 – xéq	0,20 – xéq	xéq	xéq

 

2) Q_{r, éq} = ([C₆H₅–COO–CH₃]_éq.[H₂O]_éq) / ([C₆H₅–COOH]_éq.[CH₃–OH]_éq) = x_éq² / (0,20 – x_éq)²

Q_{r, éq} = K = 4 = x_éq² / (0,20 – x_éq)² ⇒ x_éq / (0,20 – x_éq) = 2 ⇒ x_éq = 0,40 – 2 x_éq

x_éq = 0,40 / 3 = 0,13 mol  

Remarque : La valeur de K est donnée avec un seul chiffre significatif, ce qui est insuffisant !!

On devrait donc donner la valeur de x_éq avec un chiffre significatif, ce qui ne convient pas !!

 

3) Si la réaction était totale,  0,20 – x_max = 0  ⇒   x_max = 0,20 mol

taux d’avancement : τ = x_éq / x_max = 0,13 / 0,20 = 0,65 = 65 %

 

4) n(C₆H₅–COO–CH₃)_f = n(H₂O)_f = x_éq = 0,13 mol  ;

n(C₆H₅–COOH)_f = n(CH₃-OH)_f = 0,20 – x_éq = 0,20 – 0,13 = 7,0.10^-2 mol

 

5) Q_{r, éq} = ([C₆H₅–COO–CH₃]_éq.[H₂O]_éq) / ([C₆H₅–COOH]_éq.[CH₃–OH]_éq)

Q_r,éq = x'_éq² / [(0,20 – x'_éq).(0,50 – x'_éq)] = K = 4

x'_éq² = 4 ( 0,10 – 0,70 x'_éq + x'_éq²)     ;   3 x'_éq² – 2,8 x'_éq + 0,40 = 0

∆ = 2,8² – 4 x 3 x 0,40 = 3,04  ;  ∆ = 1,74

x'_{1 éq} = ( 2,8 – 1,74) / (2 x 3 ) = 0,18 mol  ; 

x'_{2 éq} = ( 2,8 + 1,74) / (2 x 3 ) = 0,76 mol   , c'est impossible car cette valeur est supérieure aux quantités initiales des réactifs. 

x'_éq = 0,18 mol

 

6) Si la réaction était totale, la quantité finale du réactif limitant serait nulle.

Pour l'ester, 0,20 – x_max = 0  ⇒  x_max = 0,20 mol. Pour l'alcool, 0,50 – x_max = 0 ⇒ x_max = 0,50 mol.

Le réactif limitant est donc l'ester et x_max = 0,20 mol

taux d’avancement : τ = x'_éq / x_max = 0,18 / 0,20 = 0,88 = 88 %

On constate qu'en augmentant une quantité d'un réactif, le taux d'avancement final augmente.

Plus la concentration des réactifs est grande, plus le taux d'avancement final augmente.

©Sciences Mont Blanc

 

 

 

Correction Polynésie Septembre 2004 - III ) Titre alcalimétrique d'une eau minérale (spe):

 

I ) Le titre alcalimétrique TA

1) Le pH de l’eau minérale correspondant à la valeur du pH du graphique pour Va = 0 mL.


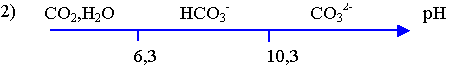
pH(eau) » 7,0

6,3 < pH(eau) < 10,3 , l'espèce prédominante est donc HCO₃^- .

3) La phénolphtaléine est incolore dans cette eau car pH < 8.

4) Par ajout d’acide chlorhydrique, le pH va diminuer, la phénolphtaléine reste incolore.

En utilisant la phénolphtaléine, on ne peut pas déterminer par l’observation un volume équivalent car la solution reste incolore

5) Si on ajoute de l'acide chlorhydrique, le pH va diminuer, aucun ion CO₃^2- n'est présent.

La valeur du TA de cette eau minérale est nulle.

II ) Le titre alcalimétrique complet TAC

1) HCO₃^-_(aq) + H₃O⁺ _(aq) = CO₂,H₂O + H₂O_(l)

2) n_a = Ca.Va = 2,0.10^-2 x 14,0.10^-3 = 2,8.10^-4 mol

Si Va = 14 mL, pH » 5 (d'après le graphique), n'_a = 10^-5 x (50 + 14).10^-3 = 6,4.10^-7 mol

Cette quantité est négligeable par rapport à celle ajoutée.

Cette réaction est rapide et totale, on peut donc l'utiliser comme réaction de dosage.

3) Le point équivalent correspond à la valeur minimum de la dérivée dpH/dVa.

D'après le graphique, V_éq = 14,5 mL et pH_éq = 4,5

4) Le vert de bromocrésol est bien adapté car pH_éq est situé dans sa zone de virage.

5) D'après l'équation de dosage, à l'équivalence, n(HCO₃^-)₀ = n_{a éq}

C.V₁ = Ca.V_éq   Þ  C = Ca.V_éq / V₁ = 2,0.10^-2 x 14,5.10^-3 / 50.10^-3 = 5,8.10^-3 mol.L^-1

6) T = C.M(CO₃^2-) = 5,8.10^-3 x (12 + 3 x 16) = 0,35 g.L^-1 

7) Ca.Va = C.Veau  Þ  Va = C.Veau / Ca = 5,8.10^-3 x 100 / 2,0.10^-2 = 29 mL

D'après la définition, TAC = 29

 

©Sciences Mont Blanc