Correction Bac Antilles Juin 2005

 

I ) Jeu de fête foraine (5,5 points)

II ) Détermination d'une constante d'équilibre par deux méthodes (6,5 points)

III ) Sonde thermique (4 points)

III ) Modulation d'amplitude (spe) (4 points)

 

Antilles Juin 2005 - I ) Jeu de fête foraine :

I ) Propulsion de la bille :

1) énergie potentielle élastique  : Epe = ½ k .( l - l₀ )²    ; ½ l – l₀ ½ = ½x ½

( l₀ :longueur du ressort au repos ; l : longueur du ressort à l'instant t)

Epe(A') = ½ k . x_A' ² = ½ x 25 x (10.10^-2)² = 0,125 J » 0,12 J

 

2) La bille lors de la détente du ressort acquiert de l'énergie cinétique.

Ec = ½ m.v²   ( m : masse en kg ;  v : vitesse en m.s^-1  )

 

3) énergie mécanique du système {ressort-bille} : Em = Epe + Epp + Ec

Epp = 0 J  ;   Em = ½ k . x² + ½ m . v² = ½ k . x² + ½ m . x '²

Ec(A') = 0 J  (v(A') = 0 m.s^-1  )  ;  Em(A') = Epe(A') = 0,125 J » 0,12 J

 

4) Si les frottements sont négligeables, l'énergie mécanique se conserve.

 

5) Em(O) = Em(A')   ;    Ec(O) + Epe(O) = Ec(A') + Epe(A')

Epe(O) = 0 J  car x = 0 m      ;     Ec(O) = Epe(A') =0,125 J » 0,12 J

 

6) v = (2 Ec/m) ; v_O = (2 Ec(O)/m) = (2 x 0,125 / 10.10^-3 ) = (0,25.10²) = 5,0 m.s^-1 

 

7) Les forces appliquées à la bille entre O et C sont le poids P verticale vers le bas et la réaction normale du plan R verticale vers le haut. (On néglige les frotements)

On applique le théorème de l'énergie cinétique entre O et C dans le référentiel terrestre supposé galiléen  :  Ec(C) – Ec(O) = W_OC(P) + W_OC(R) = 0 J

P  et R sont verticales, perpendiculaires au déplacement OC, leur travail est donc nul.

Ec(C) = Ec(O)  ;  v_C = v_O = 5,0 m.s^-1 

II ) Chute de la bille :

1) On néglige les frottements de l'air et la poussée d'Archimède de l'air.

La seule force appliquée à la bille est le poids P , elle est en chute libre.

On applique la deuxième loi de Newton dans le référentiel terrestre supposé galiléen :

m. a = P = m. g   ;    a = g

 

2) g  = - g . j    ;   a = - g . j    ;  a_x = 0 et a_y = - g

 

3) On intègre les expressions précédentes :   a_x = dv_x/dt = 0  ;   v_x = constante = v_{x 0} = v_C   

a_y = dv_y/dt = - g   ;  v_y = - g . t + v_{y 0} = - g . t   ( v_{y 0} = 0 m.s^-1  )

On intègre une seconde fois :  v_x = dx/dt = v_C   ;   x(t) = v_C . t + x₀ = v_C . t   ( x₀ = 0 m)

v_y = dy/dt = - g . t   ;   y(t) = - ½ g . t² + y₀ = - ½ g . t² + CD

équations horaires : x(t) = v_C . t  et  y(t) = - ½ g . t² + CD

 

4) t = x(t) / v_C  .  On remplace t dans la relation y(t) = - ½ g . t² + CD    ;   ( CD = 0,05 m)

y(x) = - (g / 2v_C²) x² + CD     ;  y(x) = - (10 / (2 x 25)) x² + 0,05 = - 0,2 x² + 0,05

 

5) y(x) est nulle lorsque la bille tombe dans le trou.    0 = - 0,2 x² + 0,05  

x_trou = (0,05 / 0,2) = (25.10^-2) = 5.10^-1 = 0,5 m   ;  Elle tombe dans le trou F.

 

©Sciences Mont Blanc

 

 

 

Antilles Juin 2005 - II ) Détermination d'une constante d'équilibre par deux méthodes :

 

I ) La transformation chimique étudiée :

1) Un acide selon Brönsted est une espèce chimique capable de céder un proton H⁺.

 

2) Les deux couples acide/base mis en jeu sont : CH₃CO₂H_(aq) / CH₃CO₂^-_(aq) et H₃O⁺_(aq)/ H₂O_(l)

 

3) constante d'équilibre : K = [CH₃CO₂^-]_éq.[H₃O⁺]_éq / [CH₃CO₂H]_éq

II ) Etude pH-métrique :

1) n₁ = c₁ . V₁ = 2,7.10^-3 x 100.10^-3 = 2,7.10^-4 mol

 

2)

Equation chimique		CH3CO2H(aq) + H2O(l) = CH3CO2-(aq) + H3O+(aq)
Etat du système	Avancement (mol)	Quantités de matière (mol)
Etat initiale	x = 0	n1	excès	0	0
En cours de transformation	x	n1 – x	excès	x	x
Etat final si transformation limitée	x = xf	n1 – x	excès	xf	xf
Etat final si transformation totale	x = xmax	n1 – x	excès	xmax	xmax

 

L'acide éthanoïque est le réactif limitant puisque l'eau est en excès.

Si la réaction était totale, n(CH₃CO₂H)_f = 0 = n₁ – x_max  ; x_max = n₁ = 2,7.10^-4 mol

 

3) [H₃O⁺]_f = 10^-pH = 10^-3,70 = 2,0.10^-4 mol.L^-1  ( dans l'énoncé : log(2,0.10^-4) = -3,7 )

n(H₃O⁺)_f = [H₃O⁺]_f . V₁     ;  d'après le tableau ,  n(H₃O⁺)_f = x_f

x_f = [H₃O⁺]_f . V₁ = 2,0.10^-4 x 100.10^-3 = 2,0.10^-5 mol

 

4) t₁ = x_f / x_max = 2,0.10^-5 / 2,7.10^-4 = (2 / 2,7).10^-1 = 0,74.10^-1 = 7,4.10^-2 = 7,4 %

(on utilise le tableau de calculs du début du sujet: 2 / 2,7 = 0,74)

La transformation étudiée n'est pas totale, elle est limitée car t₁ < 100 %

 

5) a) D'après le tableau, [CH₃CO₂^-]_f = [H₃O⁺]_f = 2,0.10^-4 mol.L^-1 (question I.3)

 

b) [CH₃CO₂H]_f = c₁ - [CH₃CO₂H]_consommé = c₁ - [CH₃CO₂^-]_f = 2,5.10^-3 mol.L^-1

 

6) K₁ = [CH₃CO₂^-]_f.[H₃O⁺]_f / [CH₃CO₂H]_f = (2,00.10^-4)² / 2,5.10^-3 = (4 / 2,5).10^-8+3 = 1,6.10^-5

III ) Etude conductimétrique :

1) Les espèces ioniques majoritaires présentes dans cette solution sont CH₃CO₂^- et H₃O⁺ .

Les ions hydroxyde HO^-  sont négligeables d'après la valeur de pH de 3,70.

D'après l'équation, leurs concentrations molaires sont égales.

 

2) s = l(H₃O⁺) . [H₃O⁺]_f + l(CH₃CO₂^-) . [CH₃CO₂^-]_f = (l(H₃O⁺) + l(CH₃CO₂^-)) [H₃O⁺]_f

 

3) [H₃O⁺]_f = [CH₃CO₂^-]_f = s / (l(H₃O⁺) + l(CH₃CO₂^-))

[H₃O⁺]_f = [CH₃CO₂^-]_f = 5,00.10^-2 / (35,9.10^-3 + 4,1.10^-3) = 5,00.10^-2 / 40.10^-3 = 1,25 mol.m^-3

                                    = 1,25.10^-3 mol.L^-1 .

 

4) a) [CH₃CO₂^-]_f / c₂ = 1,25.10^-3 / 1,0.10^-1 = 1,25.10^-2 < 50

L'approximation n°1 est donc justifiée.

 

b) En supposant que l'approximation n°2 soit vérifiée, la dissociation de l'acide est très faible.

La transformation chimique est donc très limitée, les produits formés sont en quantité très faible

 

c) K₂ = = [CH₃CO₂^-]_f.[H₃O⁺]_f / [CH₃CO₂H]_f = (1,25.10^-3)² / 1,0.10^-1 = 1,56.10^-6 x 10¹ = 1,56.10^-5

 

d) t₂ = [CH₃CO₂^-]_f / c₂ = 1,25.10^-3 / 1,0.10^-1 = 1,25.10^-2

IV ) Conclusion : Comparaison des résultats obtenus :

1) D'après le tableau, dans les deux études, on trouve la même valeur de K₁ pour des concentrations initiales en acide éthanoïque différentes.

K₁ ne dépend donc pas de la concentration initiale en acide éthanoïque.

 

2) D'après le tableau, dans les deux études, on trouve des valeurs différentes de taux d'avancement pour des concentrations initiales en acide éthanoïque différentes.

Le taux d'avancement final de la transformation chimique limitée dépend donc de l'état initial du système chimique.

 

3) Plus le taux d'avancement final t est grand, plus la quantité d'ions CH₃CO₂^-  est grande, plus l'acide est dissocié. L'affirmation 1 est donc juste.

D'après le tableau, plus la solution d'acide éthanoïque est diluée (concentration plus faible), comme dans l'étude pH-métrique, plus le taux d'avancement est grand ( t₁ > t₂ ), plus l'acide est dissocié. L'affirmation 2 est donc fausse.

       

 

©Sciences Mont Blanc

 

 

 

Antilles Juin 2005 - III ) Sonde thermique :

I ) Etalonnage de la soude :

 

1) Loi des tensions :    E = u_C + u_R

 

2) i = dq / dt   ;  u_C = q / C   ;   i = C . du_C/dt  ;  u_R = R . i = R.C.du_C/dt

E = u_C + R.C.du_C/dt

 

3) a) Si t ® ¥, e^{- t /(R.C)} ® 0,  u_C ® A .   Or  u_{C max} = E,   A = E.

 

b) A t = 0 s, u_C(0) = E + B   ( e⁰ = 1 ) . Or u_C(0) = 0 V  ;   E + B = 0  ;  B = - E  

 

c) u_C(t) = E . (1 – e^{- t / (R.C)})

 

4) a) u_R = R . i ;   [R] = U . I^-1   ;   ;   i = C.du_C/dt    ;  [C] = I . T . U^-1

[RC] = (U . I^-1).( I . T . U^-1) = T.       t est bien homogène à un temps.

 

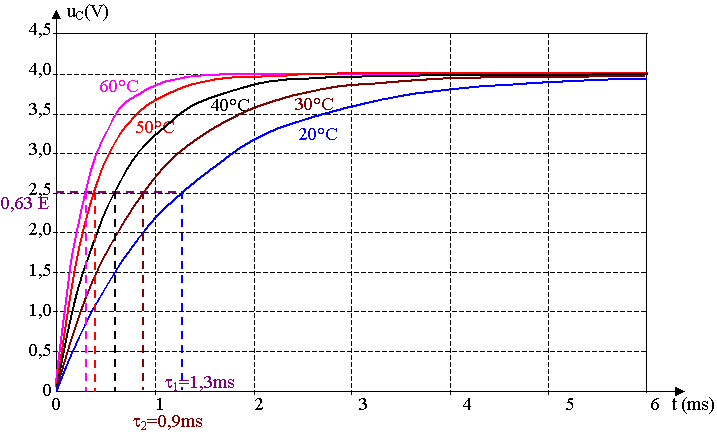
b) Pour déterminer t₁ graphiquement, on utilise la règle des 63 % :

u_C(t) = 0,63 E = 0,63 x 4,0 = 2,5 V. On reporte cette valeur sur la courbe et on lit le temps t₁ .

D'après le tracé, t₁ = 1,3 ms.

 

c) R₁ = t₁ / C = 1,3.10^-3 / 1,0.10^-6 = 1,3.10³ W = 1,3 kW

 

d)

Température q(°C)	q1 = 20	25	30	35	40	45	50	55	60
Constante de temps t (ms)	t1 = 1,3		0,9		0,6		0,4		0,3
Résistance R (k W)	R1 = 1,3	1,07	0,9	0,74	0,6	0,49	0,4	0,34	0,3

e)

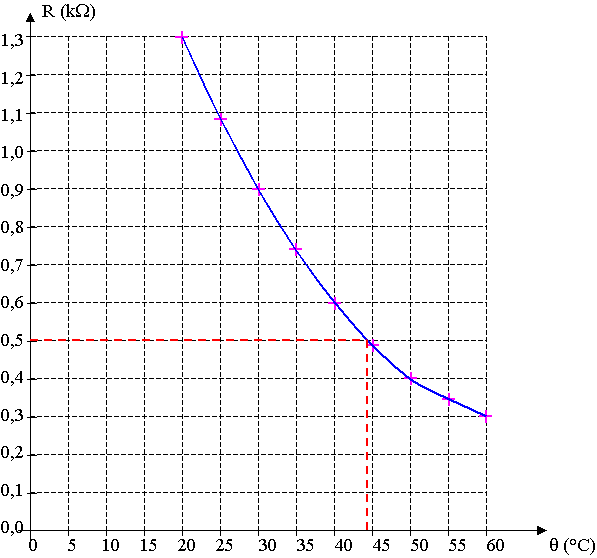
II ) Mesure d'une température :

On reporte la valeur de la résistance et on lit la température q.

D'après le graphique, q » 44,5°C

 

©Sciences Mont Blanc

 

 

 

Antilles Juin 2005 - III ) Modulation d'amplitude (spe) :

I ) La chaîne de transmission :

1) Le dispositif n°1 est le générateur HF, le n°2 est le multiplieur, le n°3 est l'amplificateur HF et le n°4 est l'antenne.

 

2) Le signal en B est le signal modulant BF noté u_S(t) + U₀ ,   celui en C est la porteuse notée u_P(t) = U_{P (max)}.cos(2p.F.t)  et celui en D est le signal modulé noté u_m(t)

 

3) La boîte noire est intercalée entre les points A et B est un dispositif qui amplifie le signal et qui ajoute une composante continue. (le microphone donne un signal électrique assez faible)

 

4) Le dispositif électrique (2) effectue une multiplication : (u_S(t) + U₀) x u_P(t)

II ) La modulation d'amplitude :

1)

 
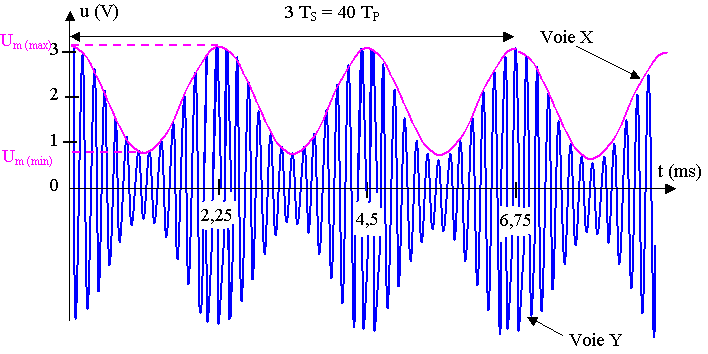
D'après le graphique, 3 T_S = 40 T_P = 6,75 ms

T_S = 6,75/3 = 2,25 ms   et  T_P = 6,75 / 40 = 0,169 ms

 

2) f = 1 / T    ( f en Hertz et T en s)

f = 1 / T_S = 1 / 2,25.10^-3 = 10³ x 0,444 = 444 Hz       

F = 1 / T_P = 1 / 0,169.10^-3 = (40 / 6,75).10³ = 5,93.10³ Hz = 5,93 kHz

 

3) a) D'après le graphique, la tensions maximale U_{m (max)} est voisine de 3,2 V et la tension minimale U_{m (min)} de 0,8 V.

 

b) m = ( 3,2 – 0,8 ) / (3,2 + 0,8) = 2,4 / 4 = 0,6

 

c) Si le taux de modulation était supérieure à 1, on aurait un phénomène de surmodulation.

 

4) a) Le taux de modulation m est inférieure à 1 si U_{S (max)} < U₀

 

b) Pour obtenir une bonne modulation, il faut que la fréquence F de la porteuse soit très grande devant celle du signal à moduler f.

 

c) f₂ = F ,  f₁ = F – f  et  f₃ = F + f

 

 

 

 

©Sciences Mont Blanc