Sujet Bac Antilles Septembre 2005

Calculatrice autorisée

Antilles Septembre 2005 - I ) Une équation au service des Sciences Physiques :

L'équation différentielle dx/dt + a.x = b (1) (1), ( a et b étant des grandeurs constantes), permet de décrire un grand nombre de phénomènes physiques variables au cours du temps: intensité, tension, vitesse, grandeur radioactive.

On rappelle que mathématiquement cette équation admet en particulier 2 solutions :

x(t) = (b / a).(1 – e^-^{a . t}) si b ¹ 0 (2) et x(t) = x₀ . e^-^{a
. t} si b = 0 avec x₀ grandeur constante

Partie A : Dans le domaine des systèmes électriques :

Cette première partie tend à montrer la validité du modèle pour un circuit électrique mettant en jeu une bobine d'inductance L et de résistance r = 11,8 W ,(donc non négligeable), et un conducteur ohmique de résistance R = 12 W, alimenté par un générateur délivrant une tension continue E = 6,1 V.

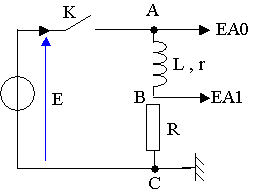
On réalise expérimentalement le circuit électrique ci-contre. L'évolution des grandeurs variables, tension u(t) et intensité i(t), est obtenue par voie informatique.

· La voie EA0 permet de visualiser la tension E

· La voie EAl permet de visualiser la tension U_Bc

Etude expérimentale

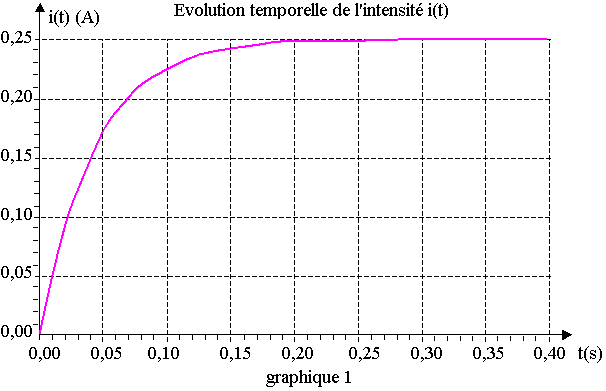
La courbe expérimentale donnant l'évolution de l'intensité i(t), obtenue par traitement informatique est donnée en Annexe n°1, graphique 1 .

Evaluer graphiquement la durée du régime transitoire. Aucune justification n'est demandée.

t étant la constante de temps associée au dipôle {bobine-conducteur ohmique} :

Donner l'expression littérale de t en fonction des paramètres du circuit.

En déduire l'expression de l'inductance de la bobine et calculer sa valeur (elle doit être comprise entre 0,95 H et 1,20 H).

Modèle théorique

En utilisant la loi d'additivité des tensions et en respectant l'orientation du circuit, établir l'équation différentielle vérifiée par l'intensité i(t).

Par identification avec l'équation (1) vérifier que a = ( R + r ) / L et donner l'expression de b.

En déduire l'équation horaire littérale i(t) en fonction de {r, R, L et E}. Montrer que cette solution valide bien l'équation établie en 2.1.

Montrer que cette équation horaire peut s'écrire i(t) = E.( 1 – e^{– t /}^t) / (R + r) .

Confrontation des résultats expérimentaux avec le modèle théorique.

On rappelle que lim_x_®_-_¥ ( e^x) = 0 et e ⁰ = 1

On appellera I l'intensité en régime permanent (l'intensité étant constante).

Donner l'expression littérale de I. Calculer sa valeur.

Est-elle en accord avec la valeur expérimentale obtenue ?

Donner l'expression littérale de i(t) à la date t = t en fonction de I. Calculer sa valeur. Est-elle en accord avec l'expérience ?

Partie B : Dans le domaine mécanique :

L'étude de la chute d'une bille d'acier, de masse m, dans un fluide de masse volumique r_fluide a été exploitée grâce à un logiciel.

Les capacités du logiciel permettent ensuite de faire tracer l'évolution de la vitesse du centre d'inertie en fonction du temps.

Les deux courbes, expérimentale et modélisée, sont proposées ci-dessous, mais ne donnent lieu à aucune exploitation.

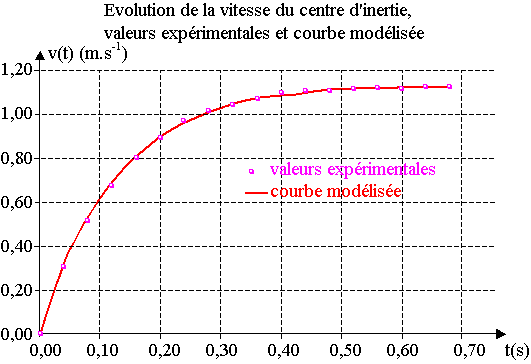
Exploitation de l'équation v(t) modélisée.

L'équation mathématique associée à la courbe modélisée, vérifie v(t) = 1,14 ( 1 – e^{– t / 0,132} ) (3) , avec v(t) en m.s^-1 et t en s. Cette équation est identifiable à l'équation (2).

Déterminer la valeur de a et du rapport b / a . Donner, sans justification, l'unité du rapport b / a .

Montrer que l'équation différentielle ayant l'équation (3) pour solution vérifie l'écriture
numérique dv/dt + 7,58 v = 8,64 .

Etude du phénomène physique.

Faire l'inventaire des forces appliquées à la bille. Les représenter sur un schéma, en sens et direction appliquée au centre d'inertie G de la bille.

Appliquer au système bille la seconde loi de Newton.

Exploitation de la modélisation

La bille ayant servi à réaliser l'étude est une bille d'acier de masse m = 32 g et de volume V.

L'accélération de la pesanteur est g = 9,81 m.s^-2.

Les forces de frottement qui s'appliquent à la bille ont pour expression f = - k. v .

En utilisant un axe vertical orienté vers le bas, montrer que l'équation différentielle relative à la grandeur variable v(t) vérifie

dv/dt + (k / m) . v = ( 1 – r_fluide . V / m ).g .

En déduire l'expression littérale des coefficients a et b de l'équation (1).

Quelle serait la valeur du coefficient b si la poussée d'Archimède était nulle ? En utilisant l'équation établie en 1.2., justifier que cette force doit être prise en compte.

Partie C : Dans le domaine de la radioactivité :

Les traceurs radioactifs sont des radio-isotopes très utilisés en imagerie médicale pour l'exploration des organes.

Des dispositifs adaptés transforment en image les mesures d'activité enregistrées.

Le ¹¹C est un traceur radioactif utilisé pour suivre en particulier l'évolution de la maladie de Parkinson.

Le traceur radioactif se fixe sur le cerveau. L'activité moyenne résiduelle évolue au cours du temps selon la loi

A(t) = A₀.e^-^{l
. t} (4).

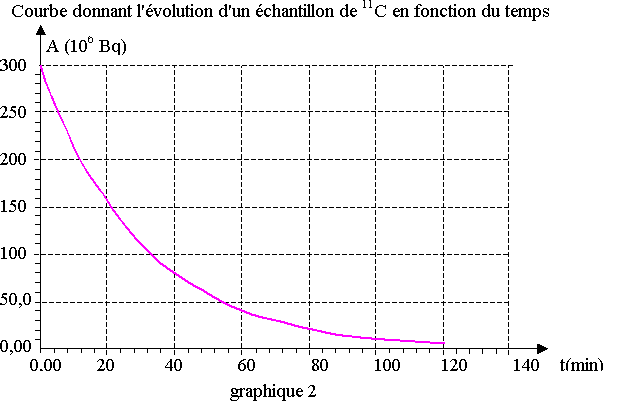
L'évolution de l'activité d'un échantillon de ¹¹C est donnée sur le graphique 2 de l'Annexe n°1.

On va utiliser ce graphique pour atteindre les grandeurs radioactives caractéristiques du ¹¹C.

Montrer par analyse dimensionnelle que l (constante radioactive), est identifiable à l'inverse d'un temps.

Rappeler la relation liant l à la constante de temps t du radio isotope.

Exprimer la loi d'évolution A(t) en fonction de t.

Evaluer graphiquement la valeur de la constante de temps t et en déduire la valeur de l.

On prendra par la suite l = 3,40.10^–2 min^-l.

Définir le temps de demi-vie t_½ , le déterminer graphiquement.

A(t) = A₀. e^-^{l . t} étant solution de l'équation différentielle dA/dt + l . A(t) = 0, on se propose d'utiliser la méthode itérative d'Euler pour résoudre cette équation.

On rappelle que pour une grandeur variable x(t), la méthode d'Euler permet d'écrire :

x(t + Dt) = x(t) + (dx/dt).Dt

Exploiter cette équation pour établir la relation liant A(t+Dt), A(t), l et Dt.

L'activité initiale de la dose injectée au patient est A₀ = A(t₀) = 3,00.10⁸ Bq.

La méthode d'Euler impose de se fixer un pas Dt pour effectuer les calculs.

Justifier que la valeur Dt = 15 min n'est pas correctement adaptée à l'étude.

On choisit de faire les calculs avec un pas Dt = 5 min. Recopier et compléter le tableau ci-dessous mettant en parallèle les résultats obtenus avec la méthode d'Euler et ceux obtenus à partir de l'équation théorique (4).

Date (min)	A _Euler (Bq)	A _théorique (Bq)
0	3,00.10⁸	3,00.10⁸
5		2,53. 10⁸
10	2,07.10⁸
15	1,72.10⁸	1,80.10⁸

On considérera que le choix de Dt est pertinent si l'écart relatif entre A _Euler et A _théorique est inférieur à 5%. La valeur proposée pour Dt vous semble-t-elle correctement adaptée ?

Annexe n°1 à rendre avec la copie

©Sciences Mont Blanc

Antilles Septembre 2005 - II ) A quoi est due la couleur des fleurs d'hortensias :

Certaines fleurs, comme celles des hortensias, possèdent des couleurs variées dues à des pigments naturels.

Les couleurs rouge, mauve, violette et bleue viennent de la présence d'anthocyanines dans les pétales.

La couleur violette est due à la molécule suivante que l'on notera HA dans la suite de l'exercice.

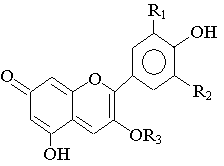
1 ) Introduction

HA peut appartenir à deux couples H₂A⁺ / HA de pKa₁ = 4,3 et HA / A^– de pKa₂ = 7

L'espèce H₂A⁺ est rouge, l'espèce HA est violette et l'espèce A^– est bleue.

On rappelle que pKe = 14.

Donner la définition d'un acide selon Brönsted.

Préciser dans chacun des 2 couples la forme acide et la forme basique.

2 ) Comportement de HA en tant qu'acide.

2.1) Ecrire l'équation de la réaction de HA en tant qu'acide avec l'eau.

2.2) Donner l'expression de la constante d'équilibre de cette réaction.

Comment appelle-t-on cette constante ? Donner sa valeur.

Le pH d'une solution contenant HA est de 10.

2.3) A partir de l'expression de K, évaluer littéralement, puis calculer le rapport [A^-]_éq / [HA]_éq

2.4) En déduire l'espèce prédominante. Conclure sur la couleur de la solution.

3 ) Comportement de HA en tant que base.

3.1) Ecrire l'équation de la réaction de HA en tant que base avec l'eau.

3.2) Donner l'expression de la constante d'équilibre K ' de cette réaction.

Quelle est la relation entre Ka₁ et K ' ?

4 ) Conclusion : Couleur des hortensias.

4.1) Placer sur un diagramme les domaines de prédominance des espèces H₂A⁺ , HA et A^– suivant les valeurs du pH.

4.2) Pourquoi les fleurs d'hortensias peuvent-elles changer de couleur suivant la nature du sol ?

©Sciences Mont Blanc

Antilles Septembre 2005 - III ) La menthe poivrée :

La menthe poivrée, calmante (maux de tête, coups de soleil) mais aussi stimulante, digestive, antispasmodique et antiseptique est bien connue pour ses bienfaits depuis des siècles.

Utilisée en parfumerie, son huile essentielle contient un ester très odorant: l'éthanoate de menthyle que l'on peut synthétiser en laboratoire, à partir de menthol et d'un acide carboxylique.

1 ) Préliminaires :

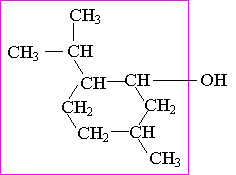Le menthol a pour formule semi-développée :

Dans la suite de l'exercice, on le notera pour simplifier R–OH

R est le groupement encadré ci-contre.

1.1) A quelle famille chimique appartient le menthol ?

1.2) Donner le nom et la formule semi-développée de l'acide carboxylique qui, par réaction avec le menthol, permet de synthétiser l'éthanoate de menthyle.

1.3) A l'aide des formules semi-développées (simplifiée pour le menthol), écrire l'équation de la réaction de synthèse de l'ester.

1.4) On mélange à l'instant initial 0,10 mol d'acide carboxylique précédent et 0,10 mol de menthol. Donner l'expression du quotient de réaction Qr et calculer sa valeur à l'instant initial.

1.5) La constante d'équilibre K associée à cette réaction est égale à 2,3 à 70°C.

Quel est le sens d'évolution spontanée du système ?

2 ) Synthèse de l'éthanoate de menthyle.

Protocole expérimental de l'expérience n°1:

Afin de synthétiser l'éthanoate de menthyle, on introduit dans un erlenmeyer maintenu dans la glace :

0,10 mol d'acide carboxylique précédent

0,10 mol de menthol

quelques gouttes d'acide sulfurique concentré

On répartit de façon égale le mélange dans 10 tubes à essais que l'on surmonte d'un réfrigérant à air. On plonge simultanément les 10 tubes dans un bain marie thermostaté à 70°C et on déclenche le chronomètre.

A intervalles de temps réguliers, on place un tube à essai dans un bain d'eau glacée et on dose l'acide restant par une solution d'hydroxyde de sodium (Na ⁺_(aq) + HO ^-_(aq)) en présence d'un indicateur coloré approprié.

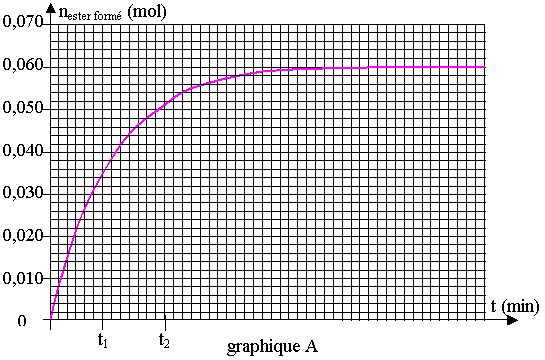
Les résultats obtenus permettent de tracer la courbe d'évolution de la quantité de matière d'ester formée en fonction du temps

( n_{ester formé} = f ( t )) donnée en Annexe graphique A :

Pourquoi faut-il placer les tubes à essais dans la glace avant titrage ? Justifier votre réponse.

Ecrire, à l'aide des formules semi-développées, l'équation de la réaction associée au titrage de l'acide carboxylique par la solution d'hydroxyde de sodium.

3 ) Exploitation des résultats :

Compléter le tableau d'avancement associé à la réaction écrite en 1.3 proposé en Annexe et à rendre avec la copie et déterminer x_max.

A l'aide de la courbe précédente, calculer le rendement de la réaction. Conclure.

Exprimer le quotient de réaction à l'équilibre en fonction de l'avancement final x_f et des quantités de matière initiales.

A l'aide de la valeur de x_f _{expérimental} déterminer la valeur de la constante d'équilibre K.

Est-elle cohérente avec celle fournie dans la partie 1 ?

Comment évaluer graphiquement la vitesse de la réaction ?

Comparer les vitesses v₁ (à t = t₁) et v₂ (à t = t₂) et justifier l'évolution de la valeur de la vitesse de la réaction au cours du temps.

4 ) Influence des conditions expérimentales :

On réalise 3 autres expériences de façon analogue à l'expérience n°1 mais en faisant varier les conditions expérimentales (température, quantité de matière initiale des réactifs) suivant le tableau ci-dessous :

Quantité de matière (en mol)	Expérience n°1	Expérience n°2	Expérience n°3
Acide carboxylique	0,10	0,10	0,20
Menthol	0,10	0,10	0,10
Température ( °C)	70	20	70

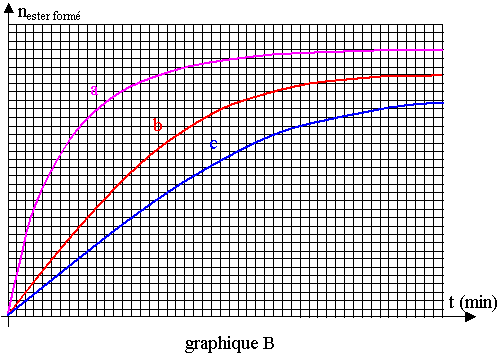
On trace à nouveau les courbes n_{ester formé} = f(t) et on obtient les allures données en Annexe graphique B :

Attribuer, en justifiant votre réponse, les courbes a, b et c aux conditions expérimentales 1, 2 et 3.

Annexe à rendre avec la copie

Equation		………… + ROH = …………
Etat	Avancement	Quantités de matière
Initial	0
Intermédiaire	x
Final	x_f

Antilles Septembre 2005 - III ) Séparation des éléments fer et cuivre (spe) :

Le minerai de cuivre contient des impuretés en particulier du fer. A partir de ce minerai, on prépare une solution aqueuse contenant des ions cuivre II (Cu²⁺_(aq)) et des ions fer III (Fe³⁺_(aq)).

Le but de l'exercice est de comparer deux méthodes possibles pour réaliser la séparation des ions Cu²⁺_(aq) des ions Fe³⁺_(aq) présents dans une même solution. Cette séparation ne nécessite pas que les éléments fer et cuivre soient en solution aqueuse à la fin des transformations envisagées.

Données : La constante de réaction K_e associée à la réaction d'autoprotolyse de l'eau

2H₂O_(l) = H₃O⁺_(aq) + HO^–_(aq) est K_e = 10^–14 (à 25°C)

Masses molaires atomiques : M(Fe) = 55,8 g.mol^–1 ; M(Cu) = 63,5 g.mol^–1.

1 ) Première partie : Une technique par précipitation :

1.1) Etude portant sur les ions Cu²⁺_(aq).

L'ajout d'une solution d'hydroxyde de sodium (Na⁺_(aq) + HO^–_(aq)) dans une solution contenant des ions Cu²⁺_(aq) donne naissance à un précipité bleu d'hydroxyde de cuivre Cu(HO)₂ _(s).

Cette transformation est modélisée par :

Cu²⁺_(aq) + 2 HO^–_(aq) = Cu(HO)_{2 (s)}

La constante de réaction K₁ associée à cette transformation est K₁ = 4,0.10¹⁸.

La formation du précipité dépend du pH de la solution.

On réalise l'expérience suivante :

Les résultats sont exploités à l'aide d'un logiciel qui permet de tracer les courbes représentant les pourcentages respectifs des espèces Cu²⁺_(aq) et Cu(HO)_{2 (s)} présentes dans la solution en fonction du pH.

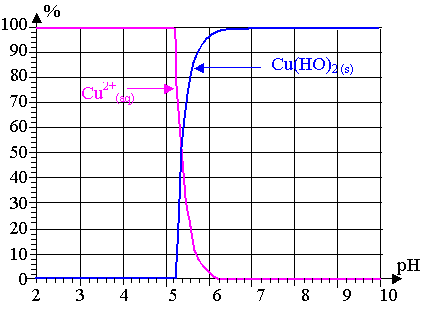
1.1.1) A l'aide de ces courbes, donner la valeur du pH pour laquelle le précipité Cu(HO)_{2 (s)} apparaît.

1.1.2) Sens d'évolution de la réaction.

1.1.2.1) Donner l'expression de K₁.

1.2.2.2) Pour un volume de solution d'hydroxyde de sodium ajouté, on peut définir le quotient de réaction noté Q_r. Exprimer Q_r.

1.2.2.3) Dans quel sens évolue la réaction si Q_r < K₁ ?

1.1.3) On étudie maintenant l'apparition du précipité. On a alors Q_r = K₁ et la concentration en ions Cu²⁺_(aq) à l'équilibre, notée [Cu²⁺_(aq)]_éq, vaut toujours 0,10 mol.L^–1 . Montrer que la valeur de la concentration en ions hydroxyde notée [HO^–_(aq)]_éq vaut 1,6.10^–9 mol.L^-1 .

1.1.4) En déduire la valeur du pH de la solution. Conclure.

1.2) Etude portant sur les ions Fe³⁺_(aq)

On réalise la même expérience en remplaçant la solution contenant des ions Cu²⁺_(aq) par une solution contenant des ions Fe³⁺_(aq) à la même concentration de 0,1 mol.L^–1.

La transformation chimique qui se déroule peut être décrite par la réaction :

Fe³⁺_(aq) + 3 HO^–_(aq) = Fe(HO)_{3 (s)}

Fe(HO)_{3 (s)} est un précipité de couleur rouille.

La courbe donnant les pourcentages respectifs des espèces Fe³⁺_(aq) et Fe(HO)_{3 (s)} présentes dans la
solution en fonction du pH de cette dernière est la suivante :

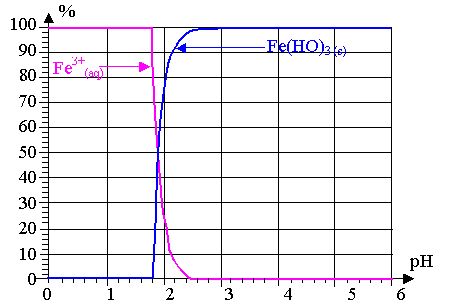
1.2.1) La solution contient-elle des ions Fe³⁺ en quantité significative pour un pH supérieur à 3,5 ?

1.2.2) On reprend le montage de la question 1.1. en plaçant dans le becher une solution constituée de :

- 10 mL de solution de chlorure de fer (III) (Fe³⁺_(aq) + 3 Cl^–_(aq))

- 10 mL de solution de sulfate de cuivre (II) (Cu²⁺_(aq) + SO₄^2–_(aq))

Dans cette solution: [Cu²⁺_(aq)] = [Fe³⁺_(aq)] = 0,1 mol.L^–1 .

Le pH du mélange initial est faible. Un élève désirant séparer les ions Cu²⁺_(aq) des ions Fe³⁺_(aq) ajoute alors la solution d'hydroxyde de sodium pour que le pH du mélange atteigne la valeur 4,0. Il filtre ensuite le mélange obtenu dans le becher, la solution obtenue est appelée S₁.

1.2.2.1) Sous quelle forme est obtenue l'espèce extraite de la solution ?

1.2.2.2) Quelle est l'espèce chimique présente dans la solution S₁ ?

1.2.2.3) Comment vérifier que la solution S₁ ne contient plus qu'une seule des espèces chimiques Cu²⁺_(aq) ou Fe³⁺_(aq) présentes initialement ?

2 ) Deuxième partie : Technique par oxydo-réduction :

Les ions cuivre (II) Cu²⁺_(aq) réagissent avec le métal fer pour donner naissance au cuivre métal et aux ions fer (II) Fe²⁺_(aq) . La transformation peut être décrite par la réaction d'équation :

Cu²⁺_(aq) + Fe_(s) = Cu _(s) + Fe²⁺_(aq) (réaction 3)

Les ions fer (III) réagissent avec le métal fer pour donner des ions fer (II) Fe²⁺_(aq).

La transformation peut être décrite par la réaction d'équation :

2 Fe³⁺_(aq) + Fe _(s) = 3 Fe²⁺_(aq) (réaction 4)

On dispose d'une solution S₁ de volume V₁ = 200 mL contenant des ions Cu²⁺_(aq) et Fe³⁺_(aq).

Dans un becher contenant la totalité de cette solution, on ajoute 10 g de fer en poudre, on estimera que cette masse est suffisante pour que la totalité des ions cuivre (II) et fer (III) réagisse.

2.1) On considère que les réactions (3) et (4) sont totales.

Sous quelle forme l'élément cuivre initialement présent dans la solution S₁ se retrouve-t-il à la fin de la réaction ?

2.2) Sous quelle forme l'élément fer initialement présent dans la solution S₁ se retrouve-t-il à la fin de la réaction.

2.3) A-t-on réalisé la séparation désirée ?

3 ) Conclusion :

On dispose d'une solution contenant des ions Cu²⁺_(aq) et des ions Fe³⁺_(aq) , ces derniers étant présents en très faible quantité. Cette solution doit être utilisée pour préparer du cuivre métallique par électrolyse des ions Cu²⁺_(aq), il est donc nécessaire d'éliminer les ions Fe³⁺_(aq).

Quelle méthode (précipitation ou oxydo-réduction) doit-on utiliser ?