Correction Sujet Bac Nouvelle Calédonie Mars 2005

Calculatrice autorisée

 

I ) La tomographie par émission de positons : Une technique d'imagerie médicale (4 points)

II ) Le dihydrogène pour la protection de l'environnement(6,5 points)

III ) Oscillateur solide-ressort (5,5 points)

I )(spe) La lunette de Kepler (4 points)

 

Nouvelle Calédonie Mars 2005 - I ) La tomographie par émission de positons : Une technique d'imagerie médicale :

1 ) La désintégration de l’oxygène 15 :

1.1) Le numéro atomique Z correspond au nombre de protons.  Z = 8

A correspond au nombre de nucléons (neutrons et protons). A = Z + N = 8 + 7 = 15

écriture symbolique du noyau d’oxygène 15 :  ¹⁵₈O

 

1.2) équation : ¹⁵₈O  ® ⁰₊₁e + ¹⁵₇N

 

1.3.1) On appelle énergie de liaison d'un noyau , notée E_l , l'énergie que le milieu extérieur doit fournir à un noyau au repos pour le dissocier en nucléons séparés au repos. E_l = Dm . c²

 

1.3.2) D'après la figure 1, la variation d’énergie DE₁ correspond à l'énergie de liaison du noyau d'oxygène 15.

DE₁ = (E_l / A)_Ox15 . A_Ox15 = 7,463 x 15 = 111,9 MeV      Cela correspond à la valeur donnée .

 

1.3.3) DE₂ = Dm.c² = (m_f – m_i) . c² = ((7 m_p + 8 m_n + m_pos) – ( 8 m_p + 7 m_n)) . c²

DE₂ = ( m_n + m_pos –m_p) . c² = (1,67492 + 0,0009109 – 1,67262).10^-27 x (2,998.10⁸)²

DE₂ = 2,886.10^-13 J = 2,886.10^-27 / 1,602.10^-19 = 1,801.10⁶ eV = 1,8 MeV

 

1.3.4) DE₃ = - (E_l / A)_N15 . A = - 7,699 x 15 = - 115,5 MeV

DE = DE₁ + DE₂ + DE₃ = 111,9 + 1,8 – 115,5 = - 1,8 MeV

2 ) L’utilisation de l’oxygène 15 en TEP

2.1) Le temps de demi-vie t_1/2 .est la durée au bout de laquelle la moitié des noyaux d'un échantillon se sont désintégrés.

 

2.2.1) N(t) = N₀. e ^{- l . t}  

A t = t_1/2 , N(t_1/2) = N₀ / 2 = N₀ . e ^{- l . t1/2} .      e ^{l . t1/2}  = 2    ;   ln (e ^{l . t1/2} ) = ln 2  ;  l . t_1/2 = ln 2

l = ln 2 / t_1/2

 

2.2.2) l = ln 2 / 123 = 5,63.10^-3 s^-1

 

2.3) N(t₁) = (5/100).N₀ = N₀ . e^{- l . t1}     ;   0,05 = e ^{- l . t1}    ;  ln(e ^{- l . t1} ) = ln 0,05

t₁ = - ln 0,05 / l = - ln 0,05 / 5,63.10^-3 = 532 s » 9 min.

 

2.4) Il faut espacer les injections d'environ 9 min mais à ce stade d'évolution, le nombre de noyaux diminue lentement, on peut donc espacer les injections de 8 à 10 min.

3 ) La détection du rayonnement gamma :

3.1) équation :  ⁰_-1e + ⁰₊₁e ® 2 g

 

3.2) DE = Dm . c² = ( 0 – m_positon - m_électron) .c² = - 2 x 9,109.10^-31 x (2,998.10⁸)² = - 1,637.10^-13 J

DE = - 1022 keV

E_photon = 1022 / 2 = 511 keV

Cette valeur est en accord avec celle donnée dans le texte .

 

©Sciences Mont Blanc

 

 

 

Nouvelle Calédonie Mars 2005 - II ) Le dihydrogène pour la protection de l'environnement:

1 ) Principe de fonctionnement d’une cellule élémentaire :

1.1) Un oxydant gagne des électrons et le réducteur en perd.

L'oxydant est donc le gaz O₂ et le réducteur est donc le gaz H₂ .

Pour écrire l'équation globale, il faut que l'oxydation et la réduction mettent en jeu le même nombre d'électrons, il faut donc multiplier l'oxydation par 2.

H_{2 (g)}  =  2 H⁺_(aq) +  2 e^–        ) x 2        ;     O_{2 (g)}  +  4 H⁺_(aq)  +  4 e^–  = 2 H₂O_(l)

2 H_{2 (g)} + O_{2 (g)} + 4 H⁺_(aq) = 4 H⁺_(aq) + 2 H₂O_(l)         Þ       2 H_{2 (g)}  +  O_{2 (g)}  = 2 H₂O_(l)

1.2) Pour l’environnement, l’avantage d’une pile à combustible est de ne produire que de l'eau et aucun polluant comme le gaz carbonique.

1.3) La réduction se produit toujours à la cathode, qui est donc l'électrode 1.

1.4)

 

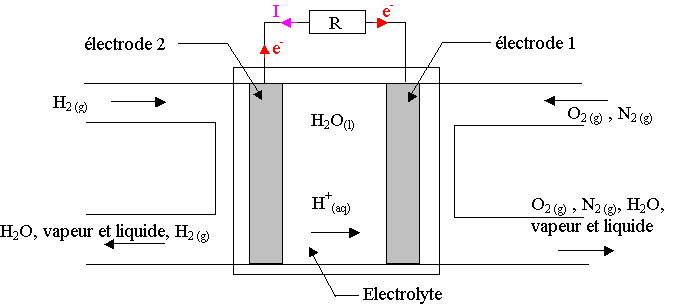
Le courant circule du pôle + de la pile vers le pôle – dans la résistance R.

Le pôle + est donc l'électrode 1 et le pôle – est donc l'électrode 2.

1.5) Un catalyseur est une espèce chimique qui accélère une réaction sans la modifier.

1.6) q = I . t = n(e^-) . N_A . e     

n(e^- ) = I . t / (N_A.e) = 300 x (192 x 60 x 60) / (6,02.10²³ x 1,6.10^-19) = 2,15.10³ mol

D'après la réduction,  n(O₂ ) = n(e^- ) / 4 = 5,38.10² mol

D'après l'oxydation, n(H₂) = n(e^- ) / 2 = 1,08.10³ mol

2 ) Principe de production du dihydrogène par électrolyse au laboratoire :

2.1.1) équation de dissolution : Na₂SO_{4 (s)} = 2 Na⁺_(aq) + SO₄^2-_(aq)  

2.1.2) n(Na₂SO₄) = c . V

2.1.3) n(Na⁺)_f = 1,0 mol = 2 x_f    ;    x_f = 0,50 mol

Si la réaction était totale, n(Na₂SO₄)_f = 0 mol.   

c . V – x_max = 0    ;    x_max = c . V = 1,0 x 500.10^-3 = 0,50 mol

x_f = x_max  , la réaction est donc totale.

2.2) Q_{r, f} =  [Na⁺]_f ² . [SO₄^2-]_f = ( 2 x_f / V )² . (x_f / V) = 4 x_f³ / V³ = 4 x 0,50³ / 0,50³ = 4,0

2.3.1) L'oxydation a toujours lieu à l’anode :                   2 H₂O_(l) =  O_{2 (g)}  +  4 H⁺_(aq)  +  4 e^–

La réduction a toujours lieu à la cathode      :       2 H₂O_(l)  +  2 e^– =  H_{2 (g)}  +  2 HO^– _(aq) 

2.3.2) A la cathode, la solution devient basique à cause des ions hydroxyde formés.

La forme basique du BBT colore la solution en bleu.

A l'anode, la solution devient acide à cause des ions H⁺_(aq) .

La forme acide du BBT colore la solution en jaune.

2.3.3) Il faut que l'oxydation et la réduction mettent en jeu le même nombre d'électrons.

                   2 H₂O_(l) =  O_{2 (g)}  +  4 H⁺_(aq)  +  4 e^–

       2 H₂O_(l)  +  2 e^– =  H_{2 (g)}  +  2 HO^– _(aq)     )  x 2

                  6 H₂O_(l) =  O_{2 (g)} + 4 H⁺_(aq) + 4 HO^-_(aq) + 2 H_{2 (g)}  

                  2 H₂O_(l) =  O_{2 (g)} + 2 H_{2 (g)}    réaction inverse de la réaction spontanée

2.3.4) En mélangeant les 2 solutions, les ions H⁺_(aq) et les ions HO^-_(aq)  forment des molécules d'eau et la solution est donc neutre. Les formes du BBT donnent une couleur verte à la solution comme au début.

©Sciences Mont Blanc

 

 

 

Nouvelle Calédonie Mars 2005 - III ) Oscillateur solide-ressort :

1 ) Etude théorique du mouvement du solide

1.1.1) Les trois forces qui s’exercent sur ce solide sont :

P  : poids du solide, vertical vers le bas,  P = m . g

R  : réaction normale du plan , verticale vers le haut

F  : force exercée par le ressort sur le solide, dans l'axe du ressort,  F = - k . x . i

 

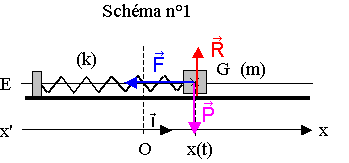
1.1.2) F = - k . x . i

Si x > 0 (cas du schéma), - k . x < 0, F et i sont bien de sens contraire.

Si x < 0 , - k . x > 0, F et i sont bien de même sens.

 

1.2.1) On applique la deuxième loi de Newton au solide dans le référentiel terrestre supposé galiléen :

F + R + P  = m . a

Projection sur l'axe Ox :    - k . x + 0 + 0 = m . a_x = m . d²x/dt² = m . x''(t)

x''(t) + (k / m). x = 0

 

1.2.2) x(t) = X_m . cos [(2p/T₀).t + j₀]     ;   x'(t) = - X_m . (2 p / T₀) . sin [(2p/T₀).t + j₀]     

x''(t) = - X_m . (2 p / T₀)² . cos [(2p/T₀).t + j₀] = - (2 p / T₀)² . x

x''(t) + (2 p / T₀)² . x = 0

D'après la question précédente,  k / m = (2 p / T₀)²

T₀ / 2 p = (m / k)     ;    T₀ = 2p (m / k)

1.2.3) [2p (m / k)] = [ m / k ] ^{1 / 2}

F = k . x   ;  [k] = [ F / x ] = [F] / L   ; 

D'après la 2ème loi de Newton,

[F] = [m.a] = M.L.T^-2

[k] =  [F] / L = M.L.T^-2 / L = M.T^-2

[2p (m / k)] = ( M / ( M.T^-2)) ^{1 / 2} = T

L’expression 2 p (m / k) est bien homogène à un temps.

2 ) Retour à l’expérience :

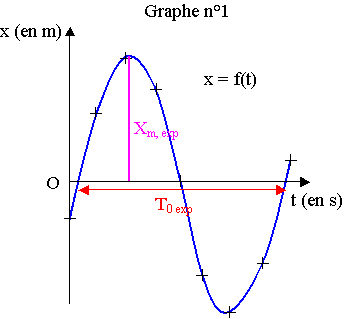
2.1)  graphe n°1

 

 

2.2) Le résultat de la modélisation de la courbe donne :   x = a.cos( b.t + c)

avec : a = 4,25.10^-2 m, b = 21,18 rad.s^-1  et c = 4,71 rad.

x = X_m . cos (2 p t / T₀ + j₀)

X_{m, exp} = a = 4,25.10^-2 m   ;    2 p / T_{0 exp} = b   ;  T_{0 exp} = 2 p / b = 2 p / 21,18 = 0,2966 s    

2.3) T₀ = 2 p (m / k) = 2 p (0,0540 / 24,0) = 0,298 s

2.4) écart relatif : ½T_0exp-T₀½/ T₀  = (0,298 – 0,2966) / 0,298 = 4,70.10^-3 = 0,47 %

Cet écart est très faible et correspond aux erreurs expérimentales.

3 ) Aspect énergétique en l’absence de frottements :

3.1) E_m = Ec + Ep él + Epp  = Ec + Ep él   ;   Epp = m . g . z = 0 J   ;   E_m = ½ m . v² + ½ k . x²

3.2) On néglige les frottements, l'énergie mécanique se conserve donc au cours du temps.

Lorsque x vaut X_m , la vitesse est nulle.  E_m = ½ k . X_m²

Lorsque x est nul, la vitesse est maximale.   E_m = ½ m . V_m²

 ½ m . V_m² = ½ k . X_m²   ;    V_m² = (k / m). X_m²   ;    V_m = X_m . (k /m) = X_m . (2 p / T₀)

V_m = 2p.X_m/ T₀

3.3) V_m = 2p.X_m/ T₀ = 2 p x 4,3.10^-2 / 0,30 = 0,90 m.s^-1 

 

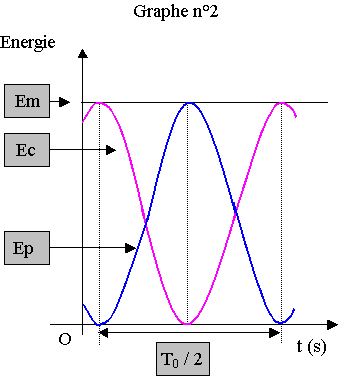
3.4) Au début, x est faible, Ep est donc faible, il s'agit donc de la courbe bleue.

L'énergie mécanique est constante, il s'agit donc de la courbe noire.

Lorsque Ep est maximale, x = x_m , la vitesse est nulle, Ec est nulle, cela correspond à la courbe rouge.

Pour déterminer la durée fléchée , on suit la courbe sur les deux graphiques.

Au début, pour x = 0, Ep = 0 J et Ec = Ec max.

Puis x augmente, Ep augmente et Ec diminue.

Pour x = x_m , v = 0 m.s^-1 ,  Ep = Ep max et  

Ec = Ec max.

Puis x diminue, Ep diminue et Ec aumente.

A nouveau x = 0, Ep = 0 J et Ec = Ec max.

Cela correspond à la durée encadrée du graphe 2 et à la durée de T₀/2 pour le graphe 1.

 

 

 

4 ) Aspect énergétique en présence de frottements :

4.1) Si on tient compte des frottements, il y a amortissement au cours du temps, le régime est alors pseudo périodique, X_m diminue à chaque oscillation.

Le temps caractéristique T correspondant est nommé pseudo période.

 

4.2.1) A t = 0s, x = X_m0 , v₀ = 0 m.s^-1  , E_m0 = Ec₀ + Ep₀ = ½ m . v₀² + ½ k . X_m0² = ½ k . X_m0²

 

4.2.2) Au bout d'une oscillation, x₁ = X_m0 / r , v₁ = 0 m.s^-1  , E_m1 = ½ k . (X_m0 / r )²

E_m1 = ½ k . X_m0² / r² = E_m0 / r²

 

©Sciences Mont Blanc

 

 

 

Nouvelle Calédonie Mars 2005 - I ) (spe)La lunette de Kepler :

©Sciences Mont Blanc