Correction Bac France - Juin 2006

 

I ) La radioactivité au service de l'archéologie ( 5,5 points)

II ) Corrosion des gouttières ( 6,5 points)

III ) Céramiques et ultrasons ( 4 points)

I ) Sons émis par une corde de violoncelle (4 points) (spe)

 

Correction Bac France - Juin 2006 - I ) La radioactivité au service de l'archéologie:

1.1) Les noyau ¹²₆C et ¹³₆C sont des isotopes car ils possèdent le même nombre de protons Z     (Z = 6) et un nombre de neutrons différents (A-Z).

1.2) Le noyau ¹⁴₆C contient 6 protons et 8 neutrons  (14 – 6 = 8)

1.3) Equation :  ¹⁴₆C ® ¹⁴₇N + ⁰_-1e

Conversation de Z :  6 = 7 – 1  ;  conservation de A :  14 = 14 + 0

La particule émise est un électron ⁰_-1^e , il s'agit donc d'une radioactivité b^-.

 

2.1.1) La transformation radioactive d'un noyau possède un caractère aléatoire.

2.1.2) La désintégration d'un noyau n'affecte pas celle d'un noyau voisin.

2.1.3) Un noyau "âgé" a autant de chances de se désintégrer qu'un noyau jeune.

2.1.4) L'évolution d'une population d'un grand nombre de noyaux radioactifs possède un caractère prévisible.

 

2.2.1) Pour les 3 expressions, N(0) = N₀.

expression (a)  :   si t ® + ¥  ,  N(t) ® 0

expression (b)  :   si t ® + ¥  ,  N(t) ® - ¥

expression (c)  :   si t ® + ¥  ,  N(t) ® + ¥

Les noyaux se désintègrent au cours du temps, N(t) diminue donc pour tendre vers 0, seule l'expression (a) convient :   N(t) = N₀ . e^{- l.t}

2.2.2) A = -dN/dt = + l.N₀.e ^{-l . t} = A₀ . e ^{- l . t}    Þ   A₀ = l . N₀

2.2.3) Le texte indique que pour 1,0 g de carbone pur, l'activité est de 13,6 désintégrations par minute, soit 0,227 désintégrations par seconde.   A(¹⁴₆C) = 0,227 Bq.

2.2.4) "L'âge zéro" correspond à la date de la mort du végétal ou de l'animal, date où l'activité vaut A₀ et commence à diminuer.

 

3.1) Le temps de demi-vie est la durée au bout de laquelle statistiquement la moitié des noyaux initialement présents a été désintégrée.  N(t_1/2) = N₀ / 2.

3.2) N(t _½ ) = N₀ / 2   Þ   N₀ . e ^{- l . t ½} = N₀ / 2      Þ  e ^{- l . t ½} = 1 / 2   Þ ln (e ^{- l . t ½} )= ln(1/2)

- l . t _½  = - ln 2   Þ  l . t _½  = ln 2

3.3) l = ln 2 / t _½  = ln 2 / 5,73.10³ = 1,21.10^-4 an^-1

3.4) A_Otzi = A₀ . e ^{- l . t1}  ;   A_Otzi / A₀ = e ^{- l . t1}  ;  A₀ / A_Otzi = e  ^{l . t1}  ;    ln(A₀/A_Otzi) =  l . t₁  

t₁ = (1 / l) . ln(A₀/A_Otzi) = (1 / 1,21.10^-4) x ln(13,6 / 7,16) = 5,30.10³ ans

3.5) Ce corail de 120 000 ans ne peut pas être daté par la méthode du "carbone 14" car d'après le texte, celle-ci a une limite de 40 000 ans, après la quantité de ¹⁴₆C est trop faible pour être mesurée avec précision.

 

4.1) N(t) = N₀ . e ^{- l . t}  Þ  N(4 t_1/2) = N₀ . e ^{- l . 4 t ½} = N₀ . e ^{– 4 ln2}

% K = N(4 t _½) / N₀ = e ^{– 4 ln2} = 2 ^{– 4} = 1 / 2⁴ = 1 / 16 = 6,25 %

4.2) %K = N(t_Terre) / N₀ = e ^{- l . t Terre} = e ^{– ln 2 . t Terre / t ½}  = 2 ^{– ( t Terre / t ½ )}

%K = 2 ^{– 4,5.10 9 / 1,3.10 9} = 2 ^–3,46 = 0,091 = 9,1 %  > 1 %

Cette méthode permet donc de mesurer l'âge de la Terre.

 

©Sciences Mont Blanc

 

Correction Bac France - Juin 2006 - II ) Corrosion des gouttières :

 

1.1)

Equation de la réaction		Zn(s)      +   2 H3O+(aq)     =  Zn 2+(aq) +  H2 (g)  +  2 H2O(l)
Etat	Avancement	Quantité de matière en mol
initial	0	n(Zn)i	n(H3O+)i	0	0	excès
en cours	x	n(Zn)i - x	n(H3O+)i  - 2 x	x	x	excès
final	xmax	n(Zn)i – xmax	n(H3O+)i -2 xmax	xmax	xmax	excès

1.2) n(Zn)_i = m(Zn)_i / M(Zn) = 0,50 / 65,4 = 7,6.10^-3 mol

n(H₃O⁺)_i = c _H3O⁺ . V = 0,40 x 75,0.10^-3 = 3,0.10^-2 mol

Si Zn est un réactif limitant , n(Zn)_f = 0 = n(Zn)_i – x_max   ;  x_max = n(Zn)_i = 7,6.10^-3 mol

Si H₃O⁺ est un réactif limitant, n(H₃O⁺)_f = 0 = n(H₃O⁺)_i – 2 x_max ; x_max= n(H₃O⁺)_i/2 = 1,5.10^-2 mol

Le réactif limitant est donc le métal zinc Zn et x_max = 7,6.10^-3 mol

1.3.1) D'après le tableau d'avancement,  n(H₂) = x   ;    x = (P – P_i) . V_gaz / (R.T)

1.3.2) x_max = (P_max – P_i) . V_gaz / (R.T)    ;    V_gaz / (R.T) = x_max / (P_max – P_i )

x = (P – P_i) . V_gaz / (R.T) = x_max . (P – P_i) / (P_max – P_i)

 

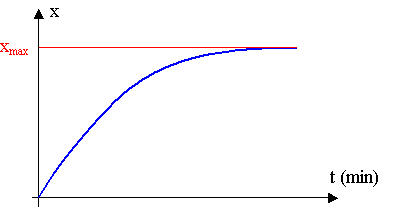
1.3.3) D'après le graphique,

x_max = 7,6 mmol = 7,6.10^-3 mol

Cette valeur correspond bien à celle trouvée à la question 1.2)

1.3.4) à t = 50,0 min, P = 1452 hPa

x = x_max . (P – P_i) / (P_max – P_i) = 7,6.10^-3 x (1452 – 1020) / (1757 – 1020) = 4,45.10^-3 mol

Cette valeur correspond à celle du graphique, à t = 50,0 min, x = 4,4 mmol.

 

 

1.4) A l'aide de la courbe, on peut déterminer dx/dt en traçant la tangente à la courbe au point étudié, dx/dt est alors égal au coefficient directeur de cette droite. On divise ensuite par V pour calculer la vitesse v.

 

2.1) En augmentant la concentration d'un réactif, on accélère la réaction.

c₂ <c₃ < c₁   Þ  v₂ < v₃ < v₁ .

La courbe (a) correspond donc à l'expérience 1 la plus rapide .

La courbe (b) correspond donc à l'expérience 3.

La courbe (a) correspond donc à l'expérience 2.

2.2.1) L'expérience 4 avec la poudre de zinc est plus rapide que l'expérience 5 avec la grenaille de zinc d'après la figure 4.

La poudre de zinc donne une plus grande surface de contact avec la solution que la grenaille où les morceaux sont plus gros.

La vitesse de réaction augmente donc si la surface de contact avec la solution est plus grande.

2.2.2) L'expérience 6 montre que la réaction est quasi nulle. Cette couche de carbonate de zinc empêche le contact entre le zinc et les ions oxonium, ce qui ralentit beaucoup la réaction.

 

3.1) [H₃O⁺] = 10^-pH = 10 ^{– 5} = 1,0.10 ^–5 mol.L^-1

3.2) Les eaux de pluie sont peu acides, ce qui ralentit la réaction. La surface de contact du zinc des gouttières est faible, il n'est pas divisé. Le métal zinc est en plus protégé par la couche de carbonate de zinc. Cela explique la longévité des gouttières en zinc.

 

©Sciences Mont Blanc

 

 

 

Correction Bac France - Juin 2006 - III ) Céramiques et ultrasons :

1.1.1) Pour plus de précisions, on mesure le maximum de périodes possibles.

D'après la figure 8, 3 T = N_S . k_S = 7,5 div  x 10 ms / div = 75 ms.     T = 75 / 3 = 25 ms.

f = 1 / T = 1 / 25.10^-6 = 40 000 Hz = 4,0.10⁴ Hz = 40 kHz

1.1.2) D'après le texte,  f_U = f = 4,0.10⁴ Hz

1.1.3) v = l / T   ;    l = v . T = 340 x 25.10^-6 = 8,5.10^-3 m

1.2.1) La valeur de la fréquence de la tension excitatrice à la résonance est égale à la fréquence des ultrasons f_U.

1.2.2) L'amplitude de vibration de la céramique varie en fonction de la fréquence de la tension excitatrice, elle est maximale à la résonance.

2.1) Ce régime est pseudo-périodique , il correspond à des oscillations amorties.

2.2) L'énergie est transférée du condensateur vers la bobine, puis de la bobine vers le condensateur et ainsi de suite.

L'amortissement des oscillations est du à la résistance, qui fait perdre de l'énergie au système par effet Joule.

2.3) Pour éviter l'amortissement, on ajoute au circuit un dispositif électronique d'entretien des oscillations, qui va compenser la perte d'énergie en apportant la même quantité d'énergie que celle perdue par effet joule.

2.4) L'affirmation 1 est fausse, si on augmente trop la résistance R, il n'y a plus d'oscillations, la tension u_C diminue jusqu'à s'annuler sans osciller, le régime est alors apériodique.

L'affirmation 2 est fausse. La période propre T₀ ne dépend que de L et C.  T₀ = 2 p . (L.C)

2.5.1) i = dq/dt  ;   q = C . u_C   ;  i = C . du_C/dt    ;   u_L = L . di/dt = L.C.d²u_C/dt²

D'après la loi des tensions,  u_C + u_L = 0    ;   u_C + L.C.d²u_C/dt² = 0    ;  d²u_C/dt² + u_C /(L.C) = 0

2.5.2) u_C(t) = U₀ . cos(2p . t / T₀ )     ;   du_C/dt = - (2p / T₀). U₀ . sin(2p . t / T₀)

d²u_C/dt² = - (2p / T₀)². U₀ . cos(2p . t / T₀)

d²u_C/dt² + u_C /(L.C) = 0    Þ   - (2p / T₀)². U₀ . cos(2p . t / T₀) + U₀. cos(2p . t / T₀)  / (L.C) = 0

Þ U₀ . cos(2p . t / T₀) . ( - (2p / T₀)² + 1 / (L.C) ) = 0

U₀ . cos(2p . t / T₀) n'est pas toujours nul, ce qui impose :   - (2p / T₀)² + 1 / (L.C)  = 0

 (2p / T₀)² = 1 / (L.C)   Þ  (T₀ / 2p)² = L.C   Þ  T₀ = 2 p (L.C)

2.5.3) C = (1 / L) . (T₀ / 2p)² = ( 25.10^-6 / (2 x 3,14))² / 1,0.10^-3 = 1,6.10^-8 F = 16 nF

 

©Sciences Mont Blanc

 

 

 

Correction Bac France - Juin 2006 - I ) Sons émis par une corde de violoncelle (spe)

 

1.1) Les modes de vibration de la corde sont appelés les modes propres.

1.2.1) L'aspect de la corde vibrant dans son mode fondamental en plein jour est un fuseau.

1.2.2) l₁ = 2 L = 2 x 0,69  = 1,38 m

 

1.3.1)  2 T₁ = N_S . k_S = 8 div x 2,5 ms/div = 20 ms    ;  T₁ = 10 ms = 1,0.10^-2 s ; f₁ = 1 / T₁ = 1 / 1,0.10^-2 = 100 Hz

1.3.2) La fréquence correspond à la hauteur du son. La fréquence est basse, le son est donc grave

 

1.4) Pour déterminer la fréquence f₁ du mode fondamental, on éclaire la corde avec un stroboscope réglé sur une grande fréquence et on diminue la fréquence jusqu'à voir plusieurs cordes immobiles puis une seule corde immobile, cette fréquence correspond à f₁.

 

1.5) v = l / T = 1,38 / 1,0.10^-2 = 138 m.s^-1 

 

1.6.1)   f₂ = 2 f₁    ;    f₃ = 3 f₁ 

1.6.2) Le pic (a) correspond au mode au mode fondamental de fréquence f₁.

Le pic (b) correspond à la fréquence f₂.     Le pic (c) correspond à la fréquence f₃.

 

1.7) f est proportionnelle à 1 / L.    f = k / L

f ' = k / L' = k / (L/2) = 2 k / L = 2 f₁

 

2.1) La hauteur du son est liée à la fréquence du son.

D'après la figure 9, la période est la même   ( 2 T = 8 x 2,5 = 20 ms)

La fréquence des 2 sons est identique, la hauteur des 2 sons est donc la même.

2.2) La forme périodique des 2 signaux est différente, ce qui signifie que le timbre des 2 sons est différent.

 

3) En comparant les figures 8 et 10, on constate que les fréquences du fondamental et des harmoniques sont doubles sur la figure 10 de celles de la figure 8. Cela signifie que la fréquence du 2^ème son est double de celle du 1^er son, le son est donc plus aigu, la hauteur est différente.

On observe aussi des différences d'intensité des harmoniques.

 

©Sciences Mont Blanc