Correction Bac Amérique du Sud Nov 2006

Calculatrice autorisée

 

I ) Détermination de la constante d'acidité d'un indicateur coloré : le vert de bromocrésol (5 points)

II ) Thermomètre de Galilée (5 points)

III ) Evolution temporelle des systèmes physique et chimique (4 points)
IV) (spe) Titrage des ions cuivre II (4 points)

 

Amérique du Sud Nov 2006 - I ) Détermination de la constante d'acidité d'un indicateur coloré : le vert de bromocrésol :


 

©Sciences Mont Blanc

 

 

 

Amérique du Sud Nov 2006 - II ) Thermomètre de Galilée :

 

1) Principe de fonctionnement

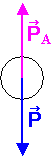
1.1) Bilan de forces : * : poids de la boule, vertical vers le bas  ; A: poussée d'Archimède verticale vers le haut.

1.2) P = m . g = ρ . Vb . g   ;      PA = mhuile . g = ρl . Vb . g  

1.3) Si la boule est immobile, on peut lui appliquer la1ère loi de Newton dans le référentiel terrestre galiléen :

+ A = 0     ;   P = PA    ;   ρ . Vb . g = ρl . Vb . g   ;   ρ = ρl

 

 

1.4) Certaines boules ont une masse volumique ρ supérieure à ρl . Le poids a une valeur supérieure à celle de la poussée d'Archimède.

Ces boules coulent donc dans l'huile et restent en bas de la colonne. D'autres boules ont une masse volumique ρ inférieure à ρl .

Le poids a une valeur inférieure à celle de la poussée d'Archimède. Ces boules montent donc dans l'huile et restent en haut de la colonne.

 

1.5) Lorsque la température du liquide s'élève, ρl diminue, PA diminue, P > PA.

La boule descend donc vers le bas.

2) Étude du mouvement d'une boule.

2.1) : poids de la boule, vertical vers le bas  ;  A :  poussée d'Archimède verticale vers le haut  et  : force de frottement de l'huile verticale vers le haut.

 

2.2) On applique la 2ème loi de Newton dans le référentiel terrestre galiléen : + A+   = m .  

Projection sur l'axe Oz :    m . aZ = m . a = P – PA – f = m . g – mhuile . g – k . v

m . dv/dt = ρ . Vb . dv/dt = ρ . Vb . g - ρl . Vb . g – k . v  = g . Vb . ( ρ - ρl) – k . v

dv/dt = g . (1 - ρl / ρ ) – (k / m) v    ;  A = g . (1 - ρl / ρ )   et   B = k / m

ρ = m / Vb = 12,0.10-3 / (4/3 π x (1,50.10-2)3) = 449kg.m-3

A = 9,80 x ( 1 – 848 / 849) = 9,5.10-3 m.s-2     ;   B = 8,8.10-3 / 12,0.10-3 = 0,73 s-1

Ces valeurs correspondent bien. Ces calculs non demandés permettent de vérifier les formules.

 

2.3) Lorsque v = vlim , la vitesse est constante.   dv/dt = 0 = A – B.vlim 

vlim = A / B = 9,5.10-3 / 0,73 = 0,013 m.s-1 

Le graphique confirme que la vitesse limite est bien de 13 mm.s-1 

 

2.4) ai = A – B . vi   et  vi+1 = vi + ai . Δt            Δt = t1 – t0 = 0,10 s

a0 = A – B x 0 = A = 9,5.10-3 m.s-2  ;    Δv(t0) = a0 . Δt = 9,5.10-3 x 0,10 = 9,5.10-4 m.s-1 

v1 = v0 + Δv(t0) = 0 + 9,5.10-4 = 9,5.10-4 m.s-1 ; a1 = A – B . v1 = 9,5.10-3 – 0,73 x 9,5.10-4 = 8,8.10-3 m.s-2

Δv(t1) = a1 . Δt = 8,8.10-4 m.s-1  ;  v2 = v1 + Δv(t1) = 9,5.10-4 + 8,8.10-4 = 18,3.10-4 m.s-1 

a2 = A – B . v2 = 9,5.10-3 – 0,73 x 18,3.10-4 = 8,2.10-3 m.s-2 ;  Δv(t2) = a2 . Δt = 8,2.10-4 m.s-1 

 

Dates t (s)

Vitesse v(tn) (m.s-1)

Δv(tn) (m.s –1)

t0= 0

0

9,5.10-4

t1 = 0,10

9,5.10-4

8,8.10 –4

t2 = 0,20

18,3.10-4

8,2.10-4

 

 

 


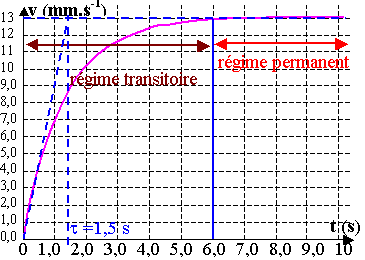
2.5) voir graphique.

 

2.6) D'après le graphique, τ = 1,5 s.

La tangente à l'origine coupe l'asymptote au temps τ.

 

2.7) Il faut choisir Δt petit par rapport au temps τ.

Plus il est petit, plus le résultat est précis mais

plus les calculs sont nombreux.

©Sciences Mont Blanc

 

 

 

Amérique du Sud Nov 2006 - III ) Evolution temporelle des systèmes physique et chimique :

 

©Sciences Mont Blanc

 

 

Amérique du Sud Nov 2006 - IV ) Titrage des ions cuivre II (spe):

 

 

 

 

©Sciences Mont Blanc