Correction Bac Liban - Juin 2008

Calculatrice autorisée

 

I ) Découverte d'une exo-planète habitable (5,5 points)

II ) Détermination expérimentale du pKa d'un indicateur coloré : Le bleu de bromophénol (6,5 points)

III ) 1932 : Le radium à la mode ... (4 points)

III ) Etude d'un piano (4 points) (spe)

 

 

Sujet complet en pdf

 

Correction Bac Liban - Juin 2008 - I ) Découverte d'une exo-planète habitable :

 

Première partie

1.1) schéma

1.2) F = G . M_C . m / (R_C+h)²

1.3) g = F / m  . A la surface de C , h = 0 m  ;  g₀ = F / m = G . M_C / R_C²

 

2.1) On applique la 2^ème loi de Newton dans le référentiel galiléen lié au centre de la planète C en utilisant le repére de Frenet : 

= m .

= _N + _T = v² /(R_C+h) . 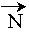+ dv/dt .    ;   = F .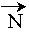

m . ( v² /(R_C+h) . 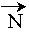+ dv/dt . ) = F . 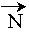     ;      m . v² / (R_C+h) =  F     et      dv/dt = 0

m . v₁² / (R_C+h) =  G . M_C . m / (R_C+h)²   ;   v₁² = G . M_C / (R_C+h)    ;   v₁ = (G . M_C / (R_C+h) )

 

2.2) Si h est négligeable devant R_C ,   v₁ = (G . M_C / R_C )

 

3) V₂ = (2 G . M / R)  ;   si R augmente V₂ diminue.

 

4.1) g₀ = G . M_C / R_C²  ;  G . M_C / R_C = g₀ . R_C   ;   V₂ = (2 g₀ . R_C)

 

4.2) V₂ = ( 2 x 22 x 9,6.10⁶) = 2,1.10⁴ m.s^-1 = 21 km.s^-1 

V₂ est supérieure à la vitesse de libération de la Terre.

 

4.3) L'existence d'une atmosphère est compromise si V₂ est faible or celle de la planète C est supérieure à celle de la Terre, l'existence d'une atmosphère sur la planète C est donc possible.

Deuxième partie :

1) M est ici la masse de l'étoile E.

 

2.1) Dans le référentiel de l'étoile E, le rapport entre le carré de la période de révolution T d’une planète autour de l'étoile et le cube du rayon r est constant :

T² / r³ = constante

 

2.2) T_c² / r_c³ = (12,93)² / (7,27.10^-2)³ = 4,35.10⁵ USI  ; T_d² / r_d³ = (84,4)² / (2,54.10^-1)³ = 4,35.10⁵ USI 

 

2.3) T_b² / r_b³ = k   ;  r_b = ³ (T_b² / k) = ³ (5,366² / 4,35.10⁵) = 4,05.10^-2 U.A.

Troisième partie :

1) "L'énergie des molécules est quantifiée" signifie que les niveaux d'énergie des molécules ont une valeur définie et distincte. Les transitions possibles entre ces niveaux d'énergie sont donc définis.

 

2) Le domaine de longueur d'onde du visible est compris entre 400 et 800 nm. 1 μm = 1000 nm

Ces radiations ont une longueur d'onde supérieure à celles du domaine visible, ce sont des radiations infra-rouges .

 

3) ΔE = E₁ – E₀ = h . ν = h . c / λ   

λ = h . c / (E₁ – E₀) = 6,626.10^-34 x 3,00.10⁸ / (0,20 x 1,6.10^-19) = 6,2.10^-6 m = 6,2 μm

 

©Sciences Mont Blanc

 

 

Correction Bac Liban - Juin 2008 - II ) Détermination expérimentale du pKa d'un indicateur coloré : Le bleu de bromophénol :

Première partie

1) n₀ = C₀ . V = 3,0.10^-5 x 0,100 = 3,0.10^-6 mol

 

2.1) Un acide selon Bronsted est une espèce chimique capable de céder un proton H⁺ .

 

2.2) couples :  HIn / In^-  et  H₃O⁺ / H₂O

 

3.1)

Equation chimique		HIn(aq)    +       H2O(l)     = In-(aq)  +    H3O+(aq)
Etat du système	Avancement	Quantité de matière en mol
Etat initial	x = 0	n0	excès	0	0
Etat intermédiaire	x	n0 - x	excès	x	x
Etat final si réaction totale	x = xmax	n0 - xmax	excès	xmax	xmax
Etat final observé	x = xf	n0 - xf	excès	xf	xf

 

3.2) L'eau est en excès, HIn est en défaut :  n₀ – x_max = 0   ;   x_max = n₀ = 3,0.10^-6 mol.

 

3.3) x_f = n(H₃O⁺)_f = [H₃O⁺] . V = 10^-pH . V = 10^-4,7 x 0,100 = 2,0.10^-6 mol

 

3.4) τ = x_f / x_max = 2,0.10^-6 / 3,0.10^-6 = 0,67 = 67 % ; τ < 1 , la réaction n'est pas totale, elle est limitée.

 

4.1) n(HIn) = n₀ – x    ;   n(In^-) = x  ;  n(HIn) = n₀ – n(In^-)   ;  n(HIn) + n(In^-)   = n₀

 

4.2) On divise la relation précédente par V :  [HIn] + [In^-] = C₀

Deuxième partie

1) Dans la solution S₁ acide, HIn espèce jaune prédomine. Dans la solution S₂ basique, In^- espèce bleue prédomine.

 

2) La proportion d'acide et de base conjuguée dépend de la concentration d'ions oxonium H₃O⁺ , du pH de la solution.

 

3) Si [HIn] est négligeable, [In^-] est égale à C₀ .

Troisième partie

1.1) D'après l'énoncé, à la longueur d'onde λ utilisée par le spectrophotomètre, seule la forme basique In^- absorbe, on a donc : A = k . [In^-].

 

1.2) Au pH de 12,0, la solution est très basique, HIn est négligeable devant In^-,  [In^-] = C₀ .

A = A_max = k . [In^-] = k . C₀ .     k = A_max / C₀ = 1,66 / 3,0.10^-5 = 5,5.10⁴ L.mol^-1

 

1.3) [In^-] = A / k = 0,83 / 5,5.10⁴ = 1,5.10^-5 mol.L^-1  

[Hin] = C₀ – [In^-] = 3,0.10^-5 – 1,5.10^-5 = 1,5.10^-5 mol.L^-1 = [In^-]

 

2.1) voir graphique

 

2.2) K_a = [H₃O⁺] . [In^-] / [HIn]  ; - log Ka = - log[H₃O⁺]+log([HIn]/[In^-])

pKa = pH + log([HIn] / [In^-])  ; pH = pKa + log([In^-] / [HIn]) 

 

2.3) Lorsque [Hin] = [In^-], log([In^-] / [HIn]) = 0 , pH = pKa.

D'après le graphique, les 2 courbes se croisent à pH = pKa = 3,9.

 

2.4) La solution S₂ a un pH de 12,0.  [H₃O⁺ ] = 1,0.10^-12 mol.L^-1

[In^-] / [HIn] = K_a / [H₃O⁺] = 10^-3,9 / 1,0.10^-12 = 1,3.10⁸ >> 10⁴

HIn est donc bien négligeable devant In^- .

 

 

 

©Sciences Mont Blanc

 

 

 

Correction Bac Liban - Juin 2008 - III ) 1932 : Le radium à la mode ... :

 

Première partie

1.1) Le noyau de radium est composé de 88 protons ( Z = 88) et de 138 neutrons (226 – 88).

 

1.2) Lois de Soddy : Lors d'une désintégration nucléaire, il y a conservation du nombre de charge Z et du nombre de nucléons A.

La particule α est ⁴₂He. Le noyau fils a donc 86 protons (88 – 2) et 222 neutrons (226 – 4).

²²⁶₈₈Ra → ²²²₈₆Rn + ⁴₂He

 

2.1) m(²²⁶Ra) = n . M = (N₀ / N_A) . M = ( 3,33.10¹⁴ / 6,02.10²³) . 226 = 1,25.10^-7 g

La phrase illustrant ce résultat est "Le Tho-Radia revendique haut et fort sa faible teneur en radium"

 

2.2.1) Loi de décroissance :  N(t) = N₀ . e^{- λ . t} 

 

2.2.2) pourcentage de noyaux restants à la date de 10 ans :

N(10ans) / N₀ = exp ( - 1,35.10^-11 x 10 x 365,25 x 24 x 60 x 60 ) = 0,996 ≈ 100 %

La quantité de radium ne varie presque pas en 10 ans, son activité reste donc la même.

 

2.3) t_1/2 = ln 2 / λ = ln 2 / 1,35.10^-11 = 5,13.10¹⁰ s = 1627 jours ≈ 16 siècles

t ½ est le temps de demi-vie, temps au bout duquel la moitié des noyaux présents initialement présents ont été désintégrés. Cela correspond bien à la phrase.

 

Deuxième partie :

1) Sur le graphique, la tangente à l'origine croise l'axe des temps au temps τ.

D'après le graphique, τ vaut 5,5 jours.

 

2) t_1/2 est le temps de demi-vie, temps au bout duquel la moitié des noyaux présents initialement présents ont été désintégrés.   A t = t_1/2 , 

N(t) = N₀ / 2  = N₀ . exp( - λ . t_1/2 ) ; exp( - λ . t_1/2 ) = 1 / 2    ;  - λ . t_1/2  = ln(1/2) 

t_1/2 = ln 2 / λ =  τ . ln 2 = 5,5 x ln 2 = 3,8 jours
Cette valeur est en accord avec l'énoncé

 

3)  N₀ = N₀' / 2  ;   τ ne change pas, la tangente à l'origine part de N₀ vers τ.

A t_1/2, N = N₀ / 2 . A 2t_1/2, N = N₀ / 4

 

 

 

©Sciences Mont Blanc

 

 

 

Correction Bac Liban - Juin 2008 - III ) Etude d'un piano :

 

 

 

 

©Sciences Mont Blanc