Sujet Bac Nouvelle Calédonie Mars 2008

Calculatrice autorisée

 

Sujet complet en pdf

 

I ) Stockage de l'énergie solaire" (6,5 points)

II ) Science et sport (5,5 points)

III ) Un conservateur alimentaire (4 points)

 

Sujet Bac Nouvelle Calédonie Mars 2008 - I ) Stockage de l'énergie solaire" :

 

Une partie de cette énergie abondante peut être transformée en énergie électrique par une cellule photovoltaïque (capteur solaire). Cette énergie électrique doit être stockée car la demande énergétique peut être décalée dans le temps vis-à-vis de l’apport en énergie solaire (utilisation par exemple, d’un éclairage la nuit).

 

Dans cet exercice, on étudie deux types de stockage de l’énergie électrique fournie par une cellule photovoltaïque :

- le stockage de l’énergie électrique dans un condensateur de grande capacité.

- la production par électrolyse d’un combustible pour une pile électrochimique.

 

Les deux parties correspondant aux deux types de stockage sont indépendantes.

La charge et la décharge du condensateur peuvent être traitées indépendamment.

1) Utilisation d’un condensateur de très grande capacité

Le fabriquant du condensateur utilisé indique une valeur de capacité C = 100 000 µF 10%.

 

1.1) Charge du condensateur à courant constant

Les caractéristiques de la cellule photovoltaïque en régime normal de fonctionnement sont indiquées ci-dessous (toutes les données ne sont pas utiles) :

Puissance : 0,6 W

Intensité : 270 mA

Tension maximale : 2,25 V

Dimensions : 394 ´ 127 ´ 20 mm

Masse : 0,41 kg

Plage de température : - 40 °C à + 60 °C

 

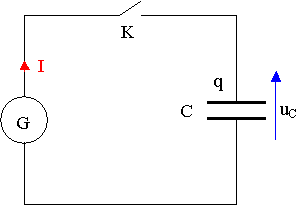La cellule photovoltaïque se comporte comme un générateur G débitant un courant d’intensité constante I = 0,27 A, tant que la tension à ses bornes reste inférieure à la tension maximale U_max = 2,25 V.

La cellule photovoltaïque est branchée aux bornes du condensateur (figure 1).

 

 

A la date t₀ = 0 s, on ferme l’interrupteur K et on débute l’enregistrement informatisé des variations de la tension aux bornes du condensateur u_C(t) en fonction du temps.

 

On obtient le graphe de la figure 2, page suivante.

 

 

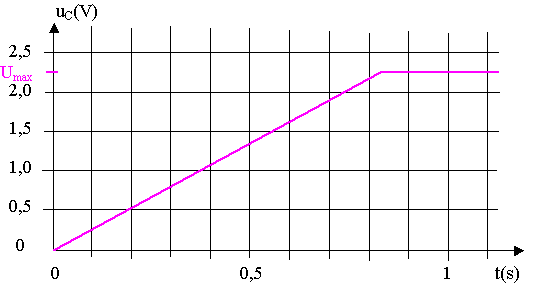
Figure 2 : charge du condensateur

 

 

1.1.1) Nommer les deux régimes observables sur le graphe u_C = f(t) représenté en figure 2.

 

1.1.2) Donner l’expression de u_C en fonction de C et de la charge q du condensateur.

 

1.1.3) Le condensateur est initialement déchargé.

Donner l’expression de la charge du condensateur q en fonction de l’intensité I et de la date t lorsque u_C est inférieure à U_max (charge à courant constant).

En déduire que u_C = I . t / C tant que u_C est inférieure à U_max.

 

1.1.4) Déterminer la valeur et préciser l’unité du coefficient directeur, noté k, de la portion de droite de la figure 2 lorsque u_C est inférieure à U_max .

Utiliser ce résultat pour vérifier que la valeur de C est compatible avec les indications du constructeur.

 

1.1.5) Calculer la quantité d’énergie électrique stockée dans le condensateur lorsque la charge est terminée.

 

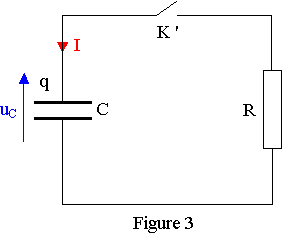1.2) Décharge du condensateur dans un conducteur ohmique

L’énergie stockée dans le condensateur peut être utilisée pour faire fonctionner une lampe (L) de faible puissance que l’on assimile à un conducteur ohmique de résistance R.

On branche en série le condensateur et le conducteur ohmique (figure 3).

 

A l’instant de date t = 0, le condensateur a une tension à ses bornes égale à U_max et on ferme l’interrupteur K’.

Le graphe donnant u_C = f(t) est donné sur la figure 4 de l’annexe.

 

 

 

1.2.1) En respectant les conventions de la figure 3, établir l’expression de i en fonction de u_C.

 

 

1.2.2) Montrer que l’expression de l’équation différentielle à laquelle satisfait u_C lors de la décharge peut s’écrire ; u_C + R.C.du_C/dt = 0.

 

1.2.3) Vérifier que u_C = U_max . e ^{– t / RC} est une solution de l’équation différentielle précédente.

 

1.2.4) Quel est le signe de i(t) lors de la décharge ? Justifier la réponse.

 

1.2.5) Déterminer, en faisant apparaître clairement la méthode sur la figure 4 de l’annexe, la valeur de la constante de temps τ du système électrique.

Déduire de la valeur de la constante de temps τ la valeur de la résistance R.

 

1.2.6) On considère que la lampe (L) fonctionne correctement si la tension imposée par le condensateur entre ses bornes est supérieure à 1,0 V.

On rappelle que l’on assimile la lampe au conducteur ohmique de résistance R.

Déterminer, en utilisant la figure 4 de l’annexe, la durée Δt durant laquelle la lampe fournit une quantité de lumière suffisante.

Conclure sur l’utilisation de ce condensateur pour un éclairage la nuit.

2) Utilisation d’une pile à combustible

L’énergie électrique fournie par une cellule photovoltaïque permet la production de dihydrogène gazeux H₂(g) par électrolyse de l’eau.

Le dihydrogène produit est stocké, puis utilisé dans une pile à combustible.

 

2.1) Electrolyse de l’eau

Afin de réaliser l’électrolyse de l’eau, les bornes de la cellule photovoltaïque sont reliées à deux électrodes de platine immergées dans une solution d’acide sulfurique. Les gaz formés sont récupérés.

L’équation modélisant la transformation ayant lieu lors de l’électrolyse est :

2 H₂O_(l) = 2H_{2 (g)} + O_{2 (g)}

 

Les couples oxydant/réducteur mis en jeu sont O_{2 (g)} / H₂O_(l) et H⁺_(aq) / H_{2 (g)}.

 

2.1.1) L’électrolyse de l’eau est-elle une transformation spontanée ? Justifier.

 

2.1.2) Ecrire les deux équations d’oxydoréduction correspondant aux transformations ayant lieu aux électrodes.

 

2.1.3) Quel type de réaction a lieu à l’électrode reliée à la borne négative de la cellule photovoltaïque ? Nommer cette électrode.

 

2.2) Fonctionnement de la pile

Après douze heures de fonctionnement, l’électrolyseur a produit une quantité de dihydrogène n(H₂) = 6,0´10 ^–2 mol. Ce dihydrogène est entièrement utilisé comme combustible dans une pile schématisée sur la figure 5 de l’annexe. La pile consomme, lors de son fonctionnement, du dihydrogène et du dioxygène gazeux qui sont introduits au contact d’électrodes poreuses séparées par une solution acide jouant le rôle d’électrolyte. Le seul produit formé est de l’eau.

L’équation modélisant la transformation ayant lieu lors du fonctionnement de la pile est :

2 H_{2 (g)} + O_{2 (g)} = 2 H₂O_(l).

 

La valeur d’un faraday est F = 9,65 ´ 10⁴ C.mol ^–1.

 

2.2.1) Indiquer sur la figure 5 donnée sur l’annexe les bornes positive et négative du générateur ainsi que la nature et le sens de circulation des porteurs de charges hors de la pile.

 

2.2.2) Donner l’expression de la quantité d’électrons n(e ^–) échangée lors de la "combustion" de la quantité n(H₂) de dihydrogène dans la pile.

En déduire la valeur de la quantité d’électricité Q échangée.

 

2.2.3) La pile permet de faire fonctionner correctement la lampe (L) avec une tension à ses bornes de 1,0 V et une intensité constante du courant de 0,70 A.

Déterminer la durée de fonctionnement de la pile pour cette intensité. Commenter ce résultat en comparant cette durée à celle obtenue à la question 1.2.6..

 

Annexe à rendre agrafée avec la copie

Annexe de l'exercice I

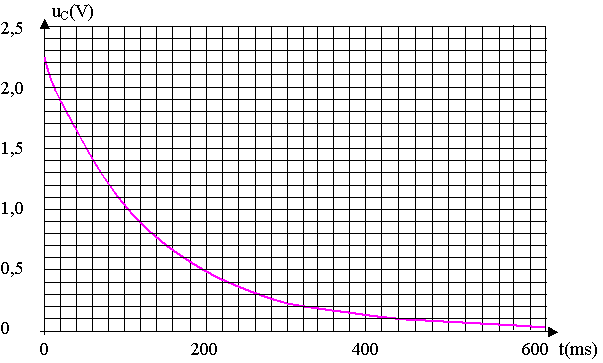
Figure 4 : décharge du condensateur.

 

 

 

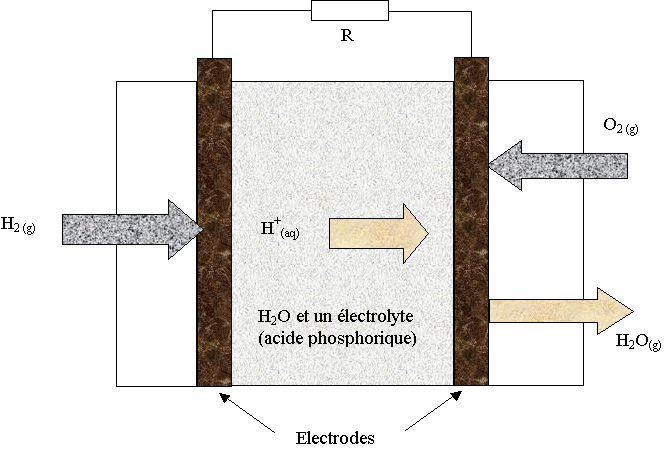
Figure 5 : fonctionnement de la pile à combustible avec un électrolyte acide

©Sciences Mont Blanc

 

 

 

Sujet Bac Nouvelle Calédonie Mars 2008 - II ) Science et sport :

Les parties 1 et 2 de cet exercice sont indépendantes.

Dans tout l’exercice le mouvement du centre d’inertie du plongeur est étudié dans le repère d’axes (Ox, Oy) représenté sur la figure 6.

Le point O est au niveau de la surface de l’eau et l’altitude du centre d’inertie G du plongeur est notée y.

On prendra pour la valeur du champ de pesanteur g = 9,80 m.s ^–2 et on considèrera que le référentiel terrestre est galiléen.

1) Saut du plongeur

Dans toute cette première partie on néglige l’action de l’air sur le plongeur au cours de son mouvement et on admet que lors du saut, les mouvements de rotation du plongeur ne perturbent pas le mouvement de son centre d’inertie G.

On note y₀ l’ordonnée du centre d’inertie du plongeur juste avant le saut et v₀ sa vitesse initiale.

On donne v₀ = 4,0 m.s ^–1 et y₀ = 4,0 m.

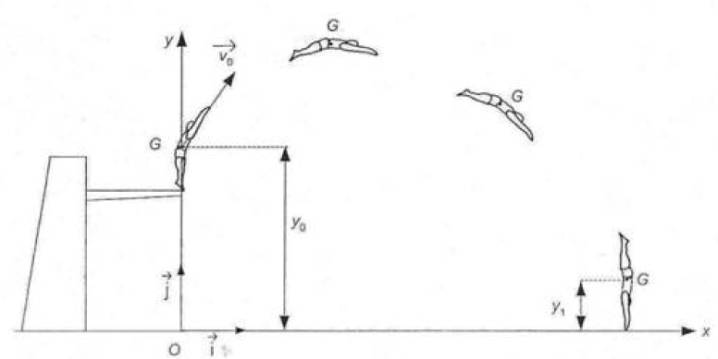
Figure 6

1.1) On considère le système {plongeur} dans le champ de pesanteur terrestre. On a représenté en figure 7, page suivante, l’évolution de l’énergie potentielle de pesanteur du système au cours du temps lors d’une partie de la phase de mouvement étudiée. On précise que la référence de l’énergie potentielle E_pp est prise au niveau de la surface de l’eau.

On rappelle que, dans ces conditions, l’énergie potentielle de pesanteur du système, à l’altitude y, a pour expression : Epp = m . g . y.

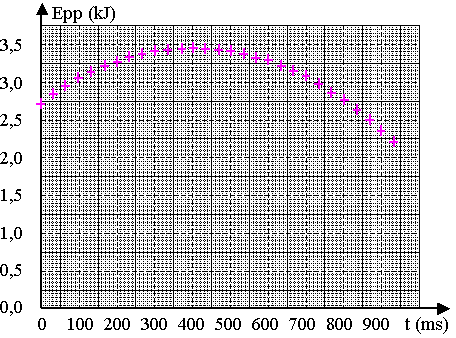
Figure 7

On note t_S la date à laquelle l’énergie potentielle de pesanteur est maximale.

En utilisant le graphique ci-dessus déterminer l’altitude y_S à laquelle se situe le centre d’inertie G du plongeur à l’instant de date t_S.

 

1.2) Le but de cette question est de déterminer la valeur de la vitesse du centre d’inertie du plongeur au moment où ses mains touchent l’eau.

 

1.2.1) Donner l’expression de l’énergie mécanique du système {plongeur en interaction avec la Terre} en fonction des grandeurs m, g, y et de la valeur de la vitesse v du centre d’inertie du plongeur.

 

1.2.2) En justifiant la réponse, dire comment cette énergie évolue au cours du temps.

On rappelle que, dans cette partie, l’action de l’air sur le plongeur est négligée.

 

1.2.3) Lorsque les mains du plongeur entrent en contact avec l’eau, le centre d’inertie du plongeur se situe à une hauteur y₁, au dessus de l’eau (voir figure 6).

A cet instant de date t₁ donner l’expression, en justifiant la réponse, de l’énergie cinétique du plongeur en fonction de v₀, m, g, y₀ et y₁.

Calculer sa valeur sachant que y₁ = 1,0 m.

 

1.2.4) En déduire l’expression de la valeur de la vitesse v₁ à l’instant de date t₁.

Calculer sa valeur.

2) Mouvement dans l’eau

Le mouvement du centre d’inertie G du plongeur est considéré comme vertical dans cette partie.

La profondeur du bassin dans lequel évolue le plongeur est de 5,0 m.

 

2.1) La figure 8 page suivante, résulte d’une simulation et représente l’évolution de l’altitude y du centre d’inertie du plongeur au cours du temps.

On précise que l’on a pris comme origine des dates l’instant où le centre d’inertie atteint la surface de l’eau.

 

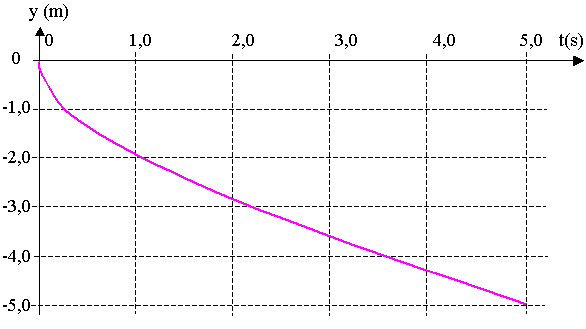
Figure 8

 

Pour pouvoir remonter, le plongeur doit redresser son buste. On estime que le plongeur agit activement pour amorcer sa remontée 1,0 s après que son centre d’inertie a atteint la surface de l’eau. De plus, on considère que le centre d’inertie du plongeur se situe toujours à 1,0 m de ses mains tendues.

Au moment où il amorce sa remontée, les mains du plongeur ont-elles atteint le fond du bassin ? Justifier la réponse.

 

2.2) On se propose de modéliser le mouvement du centre d’inertie du plongeur dans l’eau s’il n’amorçait pas de remontée. On note V le volume du plongeur et r la masse volumique de l’eau de la piscine. Le plongeur est soumis, entre autres, à une force de frottement fluide dont le sens est opposé celui du vecteur vitesse v et dont la valeur peut être modélisée par f = k . v² (où l’on considère k comme une constante).

 

2.2.1) Nommer les forces qui s’exercent sur le plongeur lors de ce mouvement.

Les représenter, sans souci d’échelle, en son centre d’inertie G.

 

2.2.2) En appliquant la deuxième loi de Newton, montrer que l’équation différentielle qui régit le mouvement du centre d’inertie du plongeur est donnée par :

dv_y/dt – (k/m).v_y² + g . (1 - r . V / m) = 0   où v_y est la composante du vecteur vitesse du centre d’inertie sur l’axe vertical orienté vers le haut. On précise que, dans le cas étudié, v = | v_y |

 

2.2.3) En déduire, en la justifiant, l’expression en régime permanent de la valeur v_l du vecteur vitesse.

 

2.2.4) Calculer v_l. On prendra r = 1,00 ´ 10³ kg.m ^–3 ; V = 6,50 ´ 10 ^–2 m³  et  k = 150 kg.m^-1.

 

2.2.5) En exploitant la figure 8, dire si le plongeur a atteint le régime permanent avant que ses mains ne touchent le fond.

On rappelle que v_y = dy/dt .

 

2.3) Une méthode de résolution numérique possible, la méthode d’Euler, permet de calculer de façon approchée la valeur algébrique de la vitesse instantanée verticale v_y à différentes dates.

On note v_y(t_n) la valeur algébrique de la vitesse à l’instant de date t_n ; la valeur algébrique v_y(t_n+1) à la date t_n+1 = t_n + Δt est calculée en utilisant la relation (1) suivante :

v_y(t_n+1) = v_y(t_n) + a_y(t_n).Δt

où a_y = dv_y/dt est la composante de l’accélération selon l’axe (Oy) et Δt est le pas de calcul.

 

Compte tenu des valeurs numériques , l’équation différentielle obtenue en 2.2.2. permet d’obtenir la relation (2) suivante :

a_y(t) = 2,14 x v_y²(t) – 0,700

La valeur du pas de calcul Δt sera choisie égale à la durée Δt = 1,20 ´ 10 ^–2 s.

En utilisant la relation (1) pour le calcul de v_y(t_n+1) et la relation (2) pour celui de a_y(t_n), compléter avec des valeurs numériques le tableau 1.

 

Tableau 1 :

 

©Sciences Mont Blanc

 

 

 

Sujet Bac Nouvelle Calédonie Mars 2008 - III ) Un conservateur alimentaire :

 

 

La solubilité d'une espèce chimique représente, à une température donnée, la quantité de matière maximale de cette espèce que l'on peut dissoudre par litre de solution. Il s'agit ici d'étudier l'évolution de la solubilité de l'acide benzoïque C₆H₅CO₂H_(s) dans l'eau en fonction de la température.

La solubilité de l'acide benzoïque dans l'eau augmente quand la température augmente.

Cette propriété est utilisée dans un procédé de purification des produits : la recristallisation.

 

Données : Masse molaire moléculaire de l'acide benzoïque M = 122 g.mol ^–1

 Conversion de degré celsius en kelvin : T(K) = θ(°C) + 273

1) Composition d'une solution saturée d'acide benzoïque

L'acide benzoïque se présente à l'état pur sous la forme de cristaux blancs.

La dissolution de l'acide benzoïque dans l'eau se traduit par l'équation suivante :

C₆H₅CO₂H_(s) = C₆H₅CO₂H_(aq)

Une solution saturée est obtenue lorsque l'acide benzoïque solide reste présent dans la solution.

A 24°C, on peut dissoudre au maximum 3,26 g d'acide benzoïque par litre de solution.

1.1) L'acide benzoïque appartient au couple acido-basique C₆H₅CO₂H_(aq)/C₆H₅CO₂^-_(aq).

Ecrire l'équation de la réaction entre l'acide benzoïque et l'eau.

 

1.2) Déterminer la concentration molaire apportée c dans un litre de solution saturée d'acide benzoïque à 24°C.

En déduire en utilisant la définition donnée dans le texte, la valeur de la solubilité s de l'acide benzoïque à 24°C exprimée en mol.L ^–1.

 

1.3) Déterminer l'avancement maximal de la réaction de l'acide benzoïque avec l'eau dans un volume de 20,0 mL de solution saturée.

On pourra s'aider d'un tableau d'avancement.

 

1.4) Le pH de cette solution vaut 2,9. Déterminer l'avancement final puis le taux d'avancement final de la réaction.

La transformation correspondante est-elle totale ?

 

1.5) Choisir, en justifiant, la conclusion adaptée parmi les deux suivantes :

(a) dans une solution saturée d'acide benzoïque à l'équilibre, la concentration en ion benzoate est sensiblement égale à la concentration en acide benzoïque.

(b) dans une solution saturée d'acide benzoïque à l'équilibre, la concentration en acide benzoïque dans la solution à l'équilibre est sensiblement égale à la concentration apportée en acide benzoïque.

2) Titrage des solutions saturées d'acide benzoïque

Plusieurs solutions saturées d'acide benzoïque sont préparées selon le protocole suivant :

- A une masse de 0,55 g d'acide benzoïque placée dans un erlenmeyer, ajouter 100 mL d'eau distillée.

- Chauffer au bain-marie afin de dissoudre l'acide benzoïque.

- Refroidir sous courant d'eau froide jusqu'à une température supérieure de 5°C à la température θ souhaitée.

- Verser le contenu de l'erlenmeyer dans un bécher thermostaté à la température θ.

Attendre que la température se stabilise.

- Prélever un volume V_p = 20,0 mL de solution surnageante.

Placer cette solution dans un bécher thermostaté.

Différentes solutions saturées d'acide benzoïque sont ainsi obtenues à différentes températures θ allant de 24°C à 50°C.

Chacune des solutions est titrée par une solution d'hydroxyde de sodium de concentration c_b = 5,0 ´ 10 ^–2 mol.L ^–1 ; le volume titré est V_p = 20,0 mL.

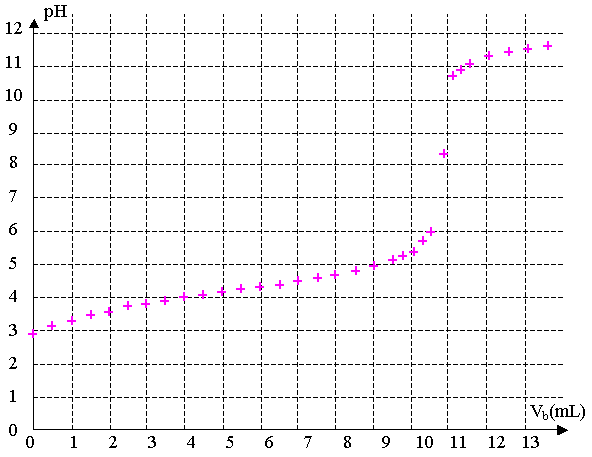
On s'intéresse ici au titrage de la solution obtenue à 24°C. La courbe obtenue lors de ce titrage donnant l’évolution du pH en fonction du volume V_b d'hydroxyde de sodium versé est représentée sur la figure 9 de l’Annexe.

 

2.1) Ecrire l'équation de la réaction modélisant la transformation ayant lieu lors du titrage de l'acide benzoïque.

 

2.2) Définir l'équivalence du titrage.

 

2.3) Déterminer par une méthode graphique que l'on fera apparaître sur la figure 9 de l'Annexe le volume V_bE de solution d'hydroxyde de sodium versé à l'équivalence.

 

2.4) Calculer la concentration molaire c d'acide benzoïque dissous dans la solution.

En déduire la valeur de la solubilité de l'acide benzoïque à 24°C.

2.5) En déduire la masse maximale d'acide benzoïque que l'on peut dissoudre dans 100 mL de solution à 24°C.

Comparer cette masse à celle introduite initialement et expliquer alors l'expression "solution saturée" employée.

3) Variation de la solubilité de l'acide benzoïque dans l'eau en fonction de la température

Les valeurs des solubilités des différentes solutions ont été mesurées suivant la même méthode, puis traitées par un tableur grapheur.

La figure 10 représente l'évolution de la solubilité s en fonction de la température T exprimée en kelvin.

 

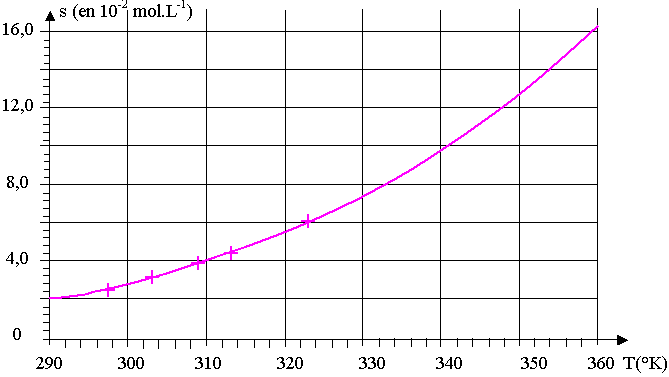
Figure 10

 

3.1) Parmi les quatre équations proposées ci-dessous, une seule peut modéliser la courbe de la figure 10. Choisir l'expression correcte. Justifier.

(1) s = a . T + b ;   (2) s = b . e ^{– a . T} ;   (3) s = b . e ^{– a / T} ; (4) s = a / T + b ; a et b étant des constantes positives.

 

3.2) A l'aide de la figure 10, déterminer la valeur de la solubilité de l'acide benzoïque s à une température de 80°C.

 

Annexe de l'exercice III

 

©Sciences Mont Blanc