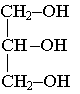Correction Bac Amérique du Nord Juin 2011

Calculatrice autorisée

 

I ) Hydrolyses des esters (6,5 points)

II ) Matière et antimatière (5,5 points)

III ) Constante de raideur d'un ressort (4 points)
IV) Réalisation d'une modulation d'amplitude (spe) (4 points)

 

Correction Bac Amérique du Nord Juin 2011 - I ) Hydrolyse des esters :

1.1.1. )

 

1.1.2. ) Cette réaction est lente , équilibrée et donc limitée.

 

1.2.1. ) Le montage à reflux permet de chauffer et ainsi accélérer la réaction tout en évitant les pertes de vapeurs de produits.

 

Schéma du montage ci-contre :

 

1.2.2. ) L’acide sulfurique est un catalyseur de la réaction.

Il permet d’accélérer la réaction sans la modifier.

 

 

 

 

 

1.3.1. )

équation chimique		ester       +       H2O        =     acide         +    alcool
État du système	Avancement (mol)	Quantités de matière (mol)
État initial	0	n0	n0	0	0
En cours	x	n0 - x	n0 - x	x	x
État final	xf	n0 - xf	n0 - xf	xf	xf

Attention , ici , l’eau n’est pas un solvant, elle n’est pas en excès.

 

1.3.2. ) τ = x_f / x_max

 

1.3.3. ) K = Q_{r, eq} = ( [acide]_eq x [alcool]_eq ) / ( [ester]_eq x [eau]_eq ) = ( x_f / V )² / ( (n₀ – x_f) / V )²

K = x_f² / (n₀ – x_f )² = x_f² / ( n₀² x ( 1 – x_f /n₀)²)

Si la réaction était totale, n(ester)_f = 0 = n₀ – x_max ;   x_max = n₀   ;  τ = x_f / n₀   ;   K = τ² / ( 1 - τ )²

 

1.3.4. ) K = τ² / ( 1 - τ )² = 1 / ( 1/τ -1 )² ;  K = 1 / ( 1/τ -1 ) ; 1 / K = 1/τ -1 

1/τ = 1 / K + 1  ;  τ = 1 / (1 / K + 1) =  1 / (1 / 0,25 + 1) = 0,33

rendement η = n_{acide obtenu} / n_{acide max} = x_f / x_max = τ = 0,33 = 33 %

 

1.4.) Si on extrait l’alcool du milieu réactionnel, l’équilibre est déplacé dans le sens direct de formation de l’acide et de l’alcool, la réaction inverse n’étant plus possible.

Le rendement η augmente.

 

2.1. )

équation chimique	RCOOR’   +       HO-        =     RCOO-    +     R’OH
Quantités en mol	n0 -x	n0 - x	x	x

n(HO^-)_restant  = n(HO^-)_initial - x

 

2.2.2. ) x = n(HO^-)_initial - n(HO^-)_restant    ;  x₄ = 10.10^-3 – 7,3.10^-3 = 2,7.10^-3 mol

x₆ = 10.10^-3 – 5,8.10^-3 = 4,2.10^-3 mol

 

2.2.3.) La réaction est totale, x_f = x_max . L’ester est le réactif limitant.

n(ester)_f = 0 = n₀ – x_max  ;  x_max = n₀ 

n₀ = m_ester / M_ester = 10,0 / 150 = 0,0667 mol ; x_f = n₀ = 0,0667 mol (avancement pour 200 mL )

Attention, le tableau présente les valeurs de x pour 20 mL de solution, soit dix fois moins.

 

2.3.1. ) t ½ est le temps au bout duquel

x = x_max / 2 = 0,0333 mol.

Pour comparer cette valeur à celle du graphique, il faut la diviser par 10 car le dosage est réalisé sur le dixième du volume de la solution .

x_{20 mL} (t ½ ) = 3,33.10^-3 mol = 3,33 mmol . D’après le graphique, t ½ = 4,6 min

 

2.3.2. ) La vitesse de réaction est proportionnelle au coefficient directeur de la tangente à la courbe, celui-ci est maximal au départ , puis il diminue au cours du temps jusqu’à s’annuler.

La vitesse évolue donc de la même façon : elle est maximale au départ, elle diminue jusqu’à s’annuler.

 

2.3.3. ) En chauffant, la réaction est plus rapide.   x_max n’est pas modifié.

La courbe violette du graphique correspond au cas où l’on chauffe.

 

3.1. )

glycérol

tributyrate de glycéryle

 

3.2. ) Le relargage permet de diminuer la solubilité du savon dans la phase aqueuse et donc de faciliter sa précipitation et sa séparation du reste du mélange.

 

 

©Sciences Mont Blanc

 

 

 

correction Bac Amérique du Nord Juin 2011 - II ) Matière et antimatière :

 

1. L’antimatière au voisinage de la Terre

1.1. Exploitation du texte :

1.1.1. E : énergie mise en jeu lors de la réaction en Joule ( J ) . m : différence entre la masse finale des noyaux produits et la masse initiale des noyaux , en kilogramme (kg).

c : célérité de la lumière dans le vide en m.s^-1  .

 

1.1.2. La relation précédente montre une équivalence entre la masse et l’énergie. La phrase du texte suggère que lorsque matière et antimatière réagissent , ils s’annihilent en convertissant la matière en énergie lumineuse.

 

1.2. Énergie créée lors de l’éruption solaire de juillet 2002 :

1.2.1. ⁰_-1e + ⁰₊₁e ➔ 2 γ

1.2.2. E = Δm x c² = ( 0 - m(⁰_-1e) - m(⁰₊₁e) ) x c² = - 2 x 9,109.0^-31 x (2,998.10⁸ )² = -1,637.10^-13 J

1.2.3. m(matière+antimatière) = 1 kg ; E = m x c² = - 1 x (2,998.10⁸ )² = - 8,988.10¹⁶ J

E_éruption = - 8,988.10¹⁶ / 3600 = - 2,497.10¹³ W.h = - 2,497.10⁴ GW.h

E_éruption / E_jour = - 2,497.10⁴ / - 1200 ≈ 21.

Cela correspond à peu près à 21 fois la consommation journalière moyenne d’énergie électrique française en 2006.

2. La création d’éléments radioactifs artificiels.

2.1. Étude de la réaction 1 :

2.1.1. Une particule alpha est un noyau d’hélium ⁴₂He

2.1.2. On utilise les lois de conservation de Soddy :

         Conservation du nombre de charge : 13 + 2 = Z + 15    ;  Z = 0.
         Conservation du nombre de masse : 27 + 4 = A + 30    ;  A = 1.
Le noyau formé est donc un neutron ¹₀n .

Equation :  ²⁷₁₃ Al  + ⁴₂ He ➔  ³⁰₁₅ P  + ¹₀n    (réaction 1)

 

2.1.3. ΔE = Δm x c² = ( m(³⁰₁₅ P)  + m(¹₀n) – m(²⁷₁₃ Al ) - m(⁴₂ He) ) x c²

2.1.4. Δm = 29,970 1 + 1,008 66 - 26,974 4 - 4,001 50 = 2,86.10^-3 u

Δm = 2,86.10^-3 x 1,66043.10^-27 = 4,75.10^{- 30} kg. ΔE = 4,75.10^{- 30} x (2,998.10⁸)² = 4,27.10^-13 J

ΔE = 4,27.10^-13 / 1,602.10^-19 = 2,66.10⁶ eV = 2,66 MeV

Cette réaction provoque un gain de masse.  Δm > 0

 

2.2. Étude de la réaction 2 :

2.2.1. On utilise les lois de conservation de Soddy :

         Conservation du nombre de charge : 15  = Z + 14    ;  Z = 1.
         Conservation du nombre de masse : 30  = A + 30    ;  A = 0.
Le noyau formé est donc un positon ¹₀e .

Equation :  ³⁰₁₅ P  ➔  ³⁰₁₄ Si + ⁰₊₁e   (réaction 2)

2.2.2. Cette réaction est spontanée. Elle se produit sans intervention extérieure, sans apport énergétique. Elle libère de l’énergie. ( E < 0 ). Elle provoque donc une perte de masse .

 

3. Décroissance radioactive du phosphore.

3.1. L’activité A(t) d’un échantillon radioactif est le nombre de désintégrations par seconde.

A(t) = A₀ x exp ( - λ x t )      avec  A₀ est l’activité initiale (à t = 0s) en Becquerel,

λ est la constante radioactive du noyau en s^-1   ; t : temps mesuré en seconde (s)

3.2. Le temps demi-vie t_1/2 est la durée au bout de laquelle la moitié des noyaux initialement présents a été désintégrée. N(t + t ½ ) = N(t) / 2  ou  A(t + t ½ ) = A(t) / 2 

A(t ½ ) = A₀ / 2 = A₀ exp ( - λ x t ½ ) ;    ½ =  exp ( - λ x t ½ ) ;  ln ½ = - λ x t ½

ln 2 = λ x t ½   ;  t ½ = ln 2 / λ

3.3. A₁ = A₀ x exp ( - λ x t₁ ) ;  ln A₁ / A₀ = - λ x t₁ = - ln 2 x t₁ / t ½

t₁ = (t ½ / ln 2) x ln (A₀ / A₁) = ( 156 / ln 2 ) x ln ( 7,2.10¹³ / 9,0.10¹² ) = 468 s = 4,7.10² s

3.4. A₀ / A₁ = 7,2.10¹³ / 9,0.10¹² = 72 / 9,0 = 8,0 = 2³   ;   A(3 t ½ ) = A₀ / 2³   

t₁ = 3 t ½ = 3 x 156 = 468 s 

©Sciences Mont Blanc

 

 

 

Correction Bac Amérique du Nord Juin 2011 - III ) Constante de raideur d'un ressort :

1. Étude statique

1.1. allongement : l₀ = L_e - L₀

1.2. Le solide est immobile dans le référentiel terrestre galiléen, on peut lui applique le principe d’inertie :   + =      où  est le poids du solide et force exercée par le ressort.

Le poids est vertical vers le bas .  P = m x g.

La forcedu ressort est vertical vers le haut car le ressort est étiré. F = k x l₀ .

 

On projète sur l’axe Ox :  P_x + F_x = 0    ;    P – F = 0

P = F   ;   m x g = k x l₀

1.3. D’après le graphique, l₀ est proportionnel à m.

l₀ = a x m.    avec a coefficient directeur de la droite.

On utilise deux points de la droite : O (0,0) et A(120,25).

a = (25.10^-2 – 0 ) / ( 120.10^-3 – 0 ) = 2,1 m.kg^-1

D’après la question 1.2. , l₀ = (g / k) x m = a x m

a = g / k ;  k = g / a = 9,8 / 2,1 = 4,7 N.m^-1

 

2. Étude dynamique

2.1.1. T₀ est la période propre des oscillations, temps pour faire une oscillation.

 

2.1.2. dx/dt = - (2 π / T₀) Xm . sin (2 π t / T₀ )  ; d²x/dt² = - (2 π / T₀)² Xm . cos (2 π t / T₀ ) 

m . d²x / dt² + k . x = - m . (2 π / T₀)² Xm . cos (2 π t / T₀ )  + k . X_m . cos(2 π t / T₀ ) = 0

X_m.cos(2 π t / T₀ ) . ( - m . (2 π / T₀)² + k ) = 0 ;  

Xm ≠ 0   ; la fonction cosinus n’est pas toujours nulle , on a donc :  ( - m . (2 π / T₀)² + k ) = 0 

k = m . (2 π / T₀)²   ;  ( k / m  ) = 2 π / T₀   ; ( m / k  ) = T₀  / 2 π  ;  T₀ = 2 π ( m / k )

 

 

2.2.1. L’amplitude du mouvement diminue au cours du temps car les frottements font perdre de l’énergie à l’oscillateur.

 

2.2.2. La pseudo-période T est-elle très proche de T₀ si l’amortissement est faible.

2.2.3. Pour que la mesure de T soit la plus précise possible, on mesure dix oscillations pour limiter l’erreur de mesure.

 

2.2.4. La courbe de la figure 2c est une droite.

Elle permet de calculer le coefficient de proportionnalité entre T₀²  et m.  T₀² = a₂ . m

On utilise deux points de la droite : O (0,0) et A(100,0,80)

a₂ = (0,80 – 0 ) / (100.10^-3 – 0) = 8,0 s².kg^-1  

D’après la question 2.1.2. , T₀² = (4 π² / k) . m

a₂ = 4 π² / k ;  k = 4 π² / a₂ = 4 x (3,14)² / 8,0 = 4,9 N.m^-1

Cette valeur est proche de celle calculée au 1.3..

 

©Sciences Mont Blanc

 

 

Correction Bac Amérique du Nord Juin 2011 - Spe - Réalisation d'une modulation d'amplitude (spe):

©Sciences Mont Blanc