Sujet Bac Polynésie Juin 2003

Calculatrice autorisée

I ) Des oscillations électriques à la cuve à ondes :

Pour étudier les ondes progressives sinusoïdales à la surface de l'eau, on utilise une cuve à ondes. Un vibreur permet de générer des ondes planes circulaires de fréquence N à la surface de l'eau. Les crêtes des vagues donnent des rides brillantes et les creux des rides sombres sur un écran que l'on photographie. Afin d'apprécier l'échelle, 2 marques A et B ont été faites sur l'écran qui correspondent à une distance AB= 7 cm dans la cuve.

A ) Etude du vibreur :

La surface de l'eau est excitée par de l'air pulsé: les pulsations sont crées par une petite pompe. Leur fréquence peut être réglée de 10 à 40 Hz grâce à un oscillateur électrique entretenu.

Les oscillations électriques peuvent être obtenues à l'aide d'un condensateur de capacité C= 30mF relié à une bobine d'auto-inductance L et de résistance r.

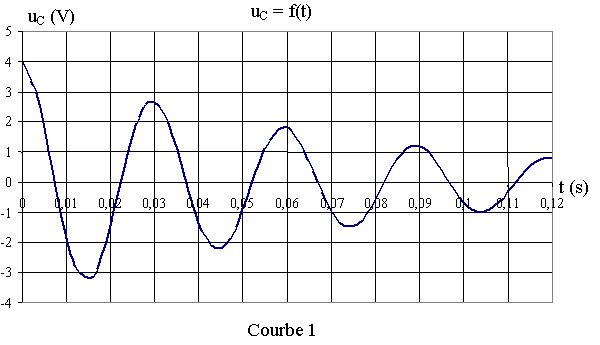
1) A l'instant t = 0 s, on relie le condensateur portant la charge Q₀ à la bobine. On peut, à l'aide d'une interface appropriée, visualiser u_C(t) : tension aux bornes du condensateur, sur l'écran d'un ordinateur et on obtient la courbe 1 ci-après :

a) u_C(t) est-elle une tension périodique ?
Comment qualifie-t-on un tel régime oscillatoire ?

b) Calculer l'énergie E₀ emmagasinée par le condensateur à t₀ =0 s.

c) Calculer l'énergie E₁ emmagasinée par le condensateur à t₁=30ms.

d) Interpréter la variation d'énergie entre les instants t₀ et t₁ .

e) Ce dispositif peut-il être utilisé pour obtenir des oscillations à la surface de l'eau ?

2) On désire entretenir les oscillations :

a) Que signifie : "entretenir les oscillations" ?

b) Pour ce faire, on introduit un montage équivalent à un dipôle D fournissant la puissance P = r.i² où r a la même valeur que la résistance de la bobine. Quel est le nouveau régime des oscillations ?

c) Quelle est alors la forme de u_C(t) ? Ce montage peut-il être utilisé pour générer des ondes sinusoïdales dans la cuve ? (Justifier)

d) Quelle est la fréquence propre des oscillations
si L = 0,75 H et C = 30 mF ?

B) Etude des ondes.

1) Mesure de la célérité des ondes :

1.1) A l'aide du vibreur, on crée des ondes progressives sinusoïdales de fréquence N à la surface de l'eau. Le phénomène observé possède une longueur d'onde l.
a) Définir la longueur d'onde.
b) Quelle relation existe-il entre la longueur d'onde l, la fréquence N et la célérité v des ondes observées ?

1.2) A l'aide de la photo 1 ci-après, déterminer le plus précisément possible la longueur d'onde l ₁ et calculer la célérité v₁ des ondes sachant que pour cette expérience 1 la fréquence des vibrations

N₁ = 8 Hz.
1.3) Une expérience 2 est réalisée à une fréquence différente N₂ = 17 Hz.

a) A l'aide de la photo 2 ci-après , montrer que la célérité des ondes varie avec la fréquence.
b) Comment appelle t-on ce phénomène ?

c) Décrire une expérience permettant d'observer ce phénomène avec des ondes lumineuses.


photo 1	photo 2

2) Influence de la profondeur de l'eau sur la célérité des ondes :

2.1) Pour étudier l'influence de la profondeur h de l'eau sur la célérité des ondes, on place sur le fond de la cuve une plaque P de plexiglas transparent. On délimite ainsi des zones de profondeur h et h' (h'<h). On génère des ondes incidentes planes sinusoïdales de fréquence N=11 Hz.

Montrer en utilisant la photo 3 que la célérité des ondes dépend de la profondeur de l'eau.

2.2) On remplace la plaque P par une plaque P', on obtient la photo 4.Quel phénomène observe-t-on ? (On pourra se référer à des phénomènes lumineux abordés en seconde)


photo 3	photo 4

2.3)

2.3.1) En eau très profonde, pour les vagues de basse fréquence, on peut démontrer que la célérité v des ondes ne dépend pratiquement plus de h. Elle varie alors proportionnellement à la période T suivant la loi : v = g .T /(2p) où g est l'intensité de la pesanteur g = 9,8 m.s^-2 . Calculer v₁ et v₂ pour les fréquences N₁ = 5,0 Hz et N₂ = 10 Hz ainsi que les longueurs d'ondes correspondantes.
2.3.2) On excite sinusoïdalement un point S à partir de l'instant t = 0 s. On observe un point M situé à 10 m de S. A quel instant t₁ le point M entre-t-il en vibration si la fréquence excitatrice est
N₁= 5 Hz ? Calculer de même l'instant t₂ pour une fréquence N₂ = 10 Hz.

2.3.3) En fait, on lance une pierre au point S ; l'ébranlement est supposé être constitué par la superposition d'ondes sinusoïdales de différentes fréquences allant de quelques Hertz à une dizaine de Hertz.

Le point M (au centre des photographies 5 et 6 ci-après) est photographié à des instants différents.


photo 5	photo 6

Donner, en le justifiant, l'ordre chronologique des deux prises de vue.

©Sciences Mont Blanc

II ) Etude cinétique par suivi spectrophotométrique :

On se propose d'étudier la cinétique de la transformation lente de décomposition de l'eau oxygénée par les ions iodures en présence d'acide sulfurique, transformation considérée comme totale. L'équation de la réaction qui modélise la transformation d'oxydoréduction s'écrit :

H₂O_{2 (aq)} + 2 I^-_(aq) + 2 H₃O⁺_(aq) = I_{2 (aq)} + 4 H₂O_(l)

La solution de diiode étant colorée, la transformation est suivie par spectrophotométrie, méthode qui consiste à mesurer l'absorbance A de la solution, grandeur proportionnelle à la concentration en diiode.

I ) Etude théorique :

1) Donner la définition d'un oxydant et celle d'un réducteur

2) Identifier dans l'équation les deux couples d'oxydoréduction mis en jeu et écrire leurs demi-équations correspondantes.

II ) suivi de la réaction :

A la date t = 0 s, on mélange 20,0 mL d'une solution d'iodure de potassium de concentration 0,1 mol.L^-1 acidifiée par l'acide sulfurique en excès, 8 mL d'eau et 2 mL d'eau oxygénée à 0,1 mol.L^-1
On remplit une cuve spectrophotométrique, et on relève les valeurs de l'absorbance au cours du temps. On détermine alors, grâce à la loi de Beer-Lambert, la concentration [I₂] du diiode formé :

t (s)	0	126	434	682	930	1178	1420	¥
[I₂] (mmol.L^-1)	0,00	1,74	4,06	5,16	5,84	6,26	6,53

1) Le mélange initial est-il stoéchiométrique ?

2) Etablir le tableau descriptif de l'évolution du système (tableau d'avancement ).

3) Etablir la relation entre [I₂] et l'avancement x de la transformation.

4) Déterminer l'avancement maximal. En déduire la valeur théorique de la concentration en diiode formé lorsque la réaction est terminée.

III ) Exploitation des résultats :

La courbe ci-après représente les variations de l'avancement x de la transformation en fonction du temps.

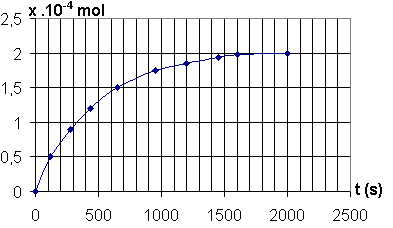
1) Donner la composition du mélange réactionnel pour t = 300 s.

2) Comment varie la vitesse volumique de réaction ? Justifier. Quel facteur cinétique peut être responsable de cette variation ?

3) Donner la définition du temps de demi-réaction, puis le déterminer.

©Sciences Mont Blanc

III ) Synthèse d'un additif alimentaire à odeur de rhum :

Le rhum est une boisson alcoolisée, fabriquée à partir de la canne à sucre. Chaque rhum a ses particularités gustatives dues à divers facteurs : variétés de cannes, lieux de cultures…

Seules certaines boissons alcoolisées, directement issues de la canne ont droit à l'appellation "rhum". L'industrie alimentaire met sur le marché de nombreux produits à odeur de rhum mais, pour des raisons économiques, beaucoup ne contiennent pas de "rhum". Ces produits tiennent leur odeur d'une molécule (notée Y) que l'on peut obtenir par synthèse.

Formule semi-développée de l'ester Y

Données :

Espèce	Masse molaire M ( g.mol^-1 )	Température d'ébullition q (°C)
A	46	101
B	46	78
Y	74	55
W	18	100

1) Transformation (N° 1) d'un mélange d'acide carboxylique (A) et d'alcool primaire (B)

1.1) Donner, en formules semi-développées, l'équation de la réaction de synthèse deY.

De façon simplifiée, elle sera notée: A + B = Y + W

1.2) Nommer Y.

Dans un ballon de 250 ml contenant 1,20 mol de B, 4 gouttes de solution d'acide sulfurique concentré ( H₂SO₄ ) et quelques grains de pierre ponce, on ajoute 1,20 mol de A (système S₁ ).

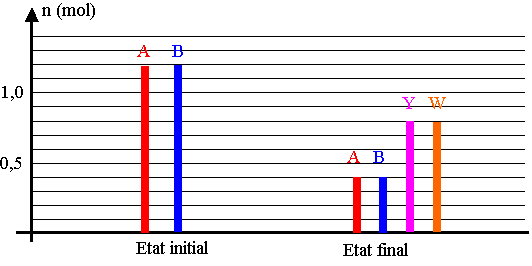
On chauffe à reflux jusqu'à l'obtention de tout l'ester possible.

1.3) Le document 1 (page 10) représente les quantités de matière des réactifs et des produits dans l'état initial et dans l'état final. L'état final est-il un équilibre chimique? Justifier.

1.4) Calculer la constante de réaction K associée à cet équilibre.

1.5) Compléter le tableau d'avancement en faisant apparaÎtre x et x_f (document 2,page 10, à rendre avec la copie).

1.6) Exprimer le quotient de réaction Q_r dans l'état intermédiaire où l'avancement est x.

1.7) Calculer l'avancement final x_f .

Montrer que ce résultat est compatible avec les valeurs du tableau.

1.8) Calculer le rendement h₁ de la transformation 1 (exprimé en pourcentage).

2) Transformation (N°2)

On considère un nouveau système S₂ , que l'on chauffe à reflux.

S₂ ne diffère de S₁ que par une donnée : on introduit 2,4 mol de A à la place de 1,2 mol.

Quand l'équilibre est atteint, un dosage montre qu'il reste 1,4 mol de A.

2.1) Calculer le nouveau rendement h₂ .

2.2) Comparer h₁ et h₂ , et justifier.

3) Transformation (N°3)

Le ballon contenant S₁ est maintenant équipé d'une colonne à distiller et d'un réfrigérant, permettant la récupération d'un distillat. En tête de colonne, un thermomètre permet de suivre la température. Celle-ci monte jusqu'à 55°C environ et se stabilise pendant un certain temps.

Lorsque la température monte à nouveau, on arrête le chauffage.

On pèse alors le distillat recueilli : m = 85,8 g.

3.1) Donner, en justifiant, la nature du distillat obtenu.

3.2) Calculer le rendement h₃.

3.3) Comparer h₁ et h₃ , justifier.

Exercice III - Document 1

Exercice III – Document 2 à compléter et à rendre avec la copie

Equation de la réaction		A + B = Y + W
Etat du système	Avancement x (mol)	n_A (mol)	n_B (mol)		n_Y (mol)	n_W (mol)
initial	0	1,20		1,20
intermédiaire	x
final	x_f