Chap 12 - Chute verticale d'un solide

I ) Force de pesanteur terrestre :

1) Poids :

Le poids d'un objet est égal à la force d'attraction gravitationnelle exercée par la Terre.

Cette force de pesanteur est caractérisée par une origine : le centre de gravité G (ou centre d'inertie) du corps, une direction : la verticale passant par G, un sens : vers le bas et une valeur : P = m . g  avec P en Newton (N), m en kg et g en N.kg^-1

2) Champ de pesanteur terrestre :

En un point donné M, au voisinage de la Terre, le poids d'un objet de masse m peut s'écrire :

  = m .    où est le vecteur champ de pesanteur terrestre au point M considéré.

 

Ce vecteur champ de pesanteur terrestre se caractérise par une origine M , une direction : la verticale passant par M, un sens : vers le bas et une valeur : l'intensité g de la pesanteur au point M

 

Remarque :La valeur de l'intensité g de la pesanteur dépend de la latitude du point M où l'on opère

g = 9,78 N.kg^-1  à l'équateur, g = 9,83 N.kg^-1  au pôle Nord, au niveau de la mer et de son altitude

(diminution d'environ 1 % tous les 30 km).

Cependant, au voisinage de la Terre (quelques kilomètres), le champ de pesanteur est uniforme :

( même direction, même sens et même valeur en tout point).

II ) Forces exercées par un fluide sur un solide en mouvement :

1) Poussée d'Archimède :

La poussée d'Archimède _A (ou ) est une force de contact sur la surface immergée du solide.

Le vecteur _A est vertical vers le haut partant du centre d'inertie C du volume de fluide déplacé .
P_A = ρ_fluide .V_immergé . g    (égal au poids du fluide déplacé).

P_A s'exprime en Newton.(N), la masse volumique du fluide ρ_fluide s'exprime en kg.L^-1 et le volume de fluide déplacé V s'exprime en L et g s'exprime en N.kg^-1

Remarque : L'air exerce aussi la poussée d'Archimède sur les objets mais son intensité est souvent négligeable par rapport aux autres forces.

2) Force de frottement fluide :

Si un solide se déplace dans un fluide, il subit une force de "frottement fluide".

Cette force est colinéaire au vecteur vitesse du solide et de sens contraire.
Souvent, elle s'oppose au mouvement, elle est résistante.

 

Sa valeur f dépend de la vitesse v du solide, de la nature du fluide, de sa forme, de son état de surface.

On peut la modéliser par une expression de la forme : f = k . vⁿ où n est un entier.

Exemples : f = k . v pour les vitesses faibles (quelques cm.s^-1) ou f = k.v² pour des vitesses plus importantes ( quelques m.s^-1).

Pour affiner le modèle, on peut aussi utiliser une expression plus complexe : f = k₁.V + k₂.V ² + ...

 

III ) Etude d'une chute verticale :

1) Chute libre :

Par définition, un solide est en chute libre s'il n'est soumis qu'à son poids.

On peut étudier la chute dans le vide, elle est parfaitement libre..

Dans l'air, un objet en chute, est soumis à la poussée d'Archimède et la force de frottements fluide, exercées par l'air, mais ces forces sont faibles et négligeables par rapport au poids dans certaines conditions : faible hauteur (quelques mètres) et faible vitesse.

2) Chute verticale libre, sans vitesse initiale : 

Une bille métallique de masse m est lâchée à 6,0 m du sol, sans vitesse initiale, d'un point pris comme origine d'un axe vertical

(O, ) orienté vers le bas. ( g = 9,80 N.kg^-1 )

a)     S'agit-il d'une chute libre ? Justifier.

b) Faire un schéma en représentant axe, origine et force(s).

c) Etablir l'équation différentielle du mouvement vérifiée par la vitesse v.

d) Déterminer les équations horaires du mouvement ( a, v et y en fonction du temps)

e)    Déterminer l’instant t₁ et la vitesse v₁ où la bille frappe le sol 

 

Réponses :

a) La poussée d'Archimède P_A dans l'air est négligeable par rapport au poids P de la bille. La vitesse de la bille et la hauteur de chute sont faibles, la force de frottement fluide exercée par l'air sur la bille est donc négligeable par rapport au poids. Le poids est donc la seule force exercée sur la bille. La chute est donc libre.

b) On étudie la bille (système) dans le référentiel terrestre galiléen, auquel on associe le repère ( O, ).

vertical vers le bas.

Force :  poids  vertical vers le bas ,   P = m . g

c) Deuxième loi de Newton : Dans un référentiel Galiléen, la somme des forces extérieures appliquées à un solide est égale au produit de la masse m du solide par l'accélération de son centre d'inertie.  

    = m .     ;    m . = m .          ⇒        =  

Dans ce cas, le mouvement est rectiligne vertical, = _y , = _y et = y . .

On projète sur l'axe   :  a = a_y = g   ;   a = dv/dt     ⇒     dv/dt = g     ( équation différentielle )

d) Pour déterminer la solution de l'équation différentielle, on cherche la fonction v qui admet g comme dérivée  : 

v = g . t + k₁   ( k₁  étant une constante)

Pour déterminer la constante k₁ , on utilise les conditions initiales :

A t = 0s, v = k₁ = v₀ = 0 m.s^-1    ⇒  v = g . t       ,   soit   dy/dt = g . t

La fonction y qui admet  g . t  comme dérivée est :  y = ½ g . t ² + k₂    ( k₂ étant une constante )

A t = 0s,  y = k₂ = y₀ = 0 m   ⇒      y = ½ g . t ²  

Equations horaires du mouvement :    y = ½ g . t²       v = g . t      et      a = g

e) Soit A le point du sol à la verticale de O, y_A = 6,0 m.      y_A = ½ g . t₁²  ;  t₁² = 2 y_A / g

t₁ = (2 y_A / g) = (2 x 6,0 / 9,80) = 1,1 s   (2 chiffres significatifs en accord avec les données)

Calcul de v₁ :   v₁ = g . t₁     ,     v₁ = 9,80 x  1,1 = 11 m.s^-1 

Dans d'autres exercices, v₀ et y₀ peuvent être non nulles, les constantes k₁ et k₂ interviennent alors.

3) Chute verticale avec force de frottement :

Etude de la chute d'une bille sans vitesse initiale, dans une éprouvette remplie d'huile .

Notations : ρ et ρ_h masses volumiques de la bille et de l'huile . V : volume de la bille.

On modélise la force de frottement fluide sous la forme : = - k.  

(Rem : k = 6 π.η.r avec η est le coefficient de viscosité du liquide et r est le rayon de la bille)

a) S'agit-il d'une chute libre ? Justifier.

b) Faire un schéma en représentant axe, origine. Faire un bilan des forces et les représenter.

Exprimer les intensités des forces en fonction des données.

c) Etablir l'équation différentielle du mouvement vérifiée par la vitesse v.

Mettre l'équation sous la forme :   dv/dt + v/τ  = k₁ .       Exprimer k₁ et τ en fonction des données.

d) Déterminer par analyse dimensionnelle les unités de k₁ et τ. Calculer les valeurs de  k₁ et τ.

e) La bille atteint-elle une vitesse limite ?  Si oui, exprimer la vitesse limite de la bille v_m puis la calculer.

Données :  k = 9,33.10^-2 S.I.  ;  ρ = 2400 kg.m^-3 ;  ρ_h = 950 kg.m^-3  ;  g = 9,80 N.kg^-1

rayon de la bille : r = 1,50 mm

Réponses :

a) La poussée d'Archimède et la force de frottement exercées par l'huile ne sont pas négligeables, le poids n'est pas la seule force exercée sur la bille, ce n'est pas une chute libre.

b) Bilan des forces exercées sur la bille :

 poids, vertical vers le bas : P = m . g = ρ . V . g

_A  poussée d'Archimède exercée par l'huile, verticale vers le haut :  P_A = m_huile . g = ρ_h .V .g

  force de frottement exercée par l'huile, verticale vers le haut (opposé au mouvement) : f = k . v

c) La bille est étudiée dans le référentiel terrestre galiléen auquel on associe le repère ( O, ).

Dans un référentiel Galiléen, on applique la 2^ème loi de Newton :   Σ _ext = m .     

  + _A + = m.  

On projète les forces sur l'axe (O, ) :     P – P_A – f  = m . a_y = m . a

ρ . V . g – ρ_h . V . g – k . v = ρ . V. dv/dt         ( on divise tout par ρ .V )

⇒   (1 - ρ_h/ρ) . g – k . v/ (ρ .V )  = dv/dt        ⇒   dv/dt + k . v / (ρ .V ) = (1 – ρ_h/ρ) . g

On a donc :  τ = ρ . V / k   et    k₁ = (1 – ρ_h/ρ) . g

d) D'après l'équation différentielle, k₁ et v / τ ont la dimension d'une accélération. k₁ est en m.s^-2 

[v / τ] = [a]    ;  [τ] = [v] / [a] = L.T^-1 / L.T^-2 = T    ;    τ est donc en s.

k₁ = (1 – ρ_h/ρ) . g = 9,80 x ( 1 - 950 / 2400) = 5,92 m.s^-2  

V = 4/3 π . r³ = 4/3 x 3,14 x (1,50.10^-3)³ = 1,41.10^-8 m³

τ  = ρ.V / k = 2400 x 1,41.10^-8 / 9,33.10^-2 = 3,63.10^-4 s

e) Si une vitesse limite est atteinte, l'accélération va s'annuler. Pour le savoir, on étudie les forces :

Le poids et la poussée d'Archimède sont constants, la force de frottement fluide augmente avec la vitesse.

Le poids  va à être compensée par la somme des deux forces résistantes _A + _lim .

La somme des forces est alors nulle, l'accélération s'annule, la vitesse reste constante, elle a atteint une valeur limite v_m .

On utilise l'équation différentielle : dv/dt + v / τ = k₁

 0 + v_m /τ = k₁    ⇒    v_m = τ. k₁ = (ρ.V / k ) . g . (1 – ρ_h/ρ) = V . g . ( ρ – ρ_h) / k

v_m = τ . k₁ = 3,63.10^-4 x 5,92 = 2,15.10^-3 m.s^-1

IV ) Résolution d'une équation différentielle par la méthode d'Euler

On cherche à résoudre une équation différentielle du type de celle obtenue précédemment :

dv/dt + v / τ = k₁  (les données sont les mêmes que précédemment)

Méthode d'Euler :

La méthode d'Euler consiste à assimiler a = dv/dt à Δv/ Δt , où Δv = v_i+1 – v_i  et Δt = t_i+1 – t_i .

Ce qui revient à considérer que sur Δt très petit, l'accélération a est constante , on a alors la courbe de la vitesse qui est une droite et égale au coefficient directeur de cette droite : a = (v_i+1 -v_i)/(t_i+1-t_i)

v_i+1 – v_i = a_i . Δt   ;   v_i+1 – v_i = a_i . Δt  

Si on choisit un pas suffisamment petit, cette hypothèse est tout à fait valable.

On utilise les conditions initiales (a₀ et v₀), puis successivement la relation  v_i+1 – v_i = a_i . Δt   et l'équation différentielle pour déterminer v_i+1 et a_i+1 .

a) Appliquer la méthode d'Euler pour un pas Δt = 1,5.10^-4 s  de 0 à 21.10^-4 s.

b) Tracer le graphique de la vitesse en fonction du temps et l'analyser .

c) Montrer que la solution de l'équation différentielle est de la forme : v = a.exp( -t / τ) + b.

Exprimer littéralement les constante a et b. Calculer leurs valeurs.

 

Réponses :

a) Avec un pas Δt = 1,50.10 ^{- 4} s, on résout de façon approchée de l'équation différentielle :

dv/dt + v / τ = k₁  ;  a + v / 3,63.10^-4  = 5,92    ⇒ a = 5,92 – 2755 v

Entre les instants t et t +Δt, la vitesse varie deΔv et l'accélération est voisine de Δv/Δt
Avec Δt = 1,50.10 ^{- 4} s et a_i = 5,92 - 2755.v_i  et Δv = v_i+1 – v_i = 1,50.10 ^{- 4}.a_i ; v_i+1 = v_i +1,50.10 ^{- 4}.a_i

A l'instant t₀ = 0 s, la vitesse initiale est nulle v₀ = 0 m.s^-1 , l'accélération initiale, a₀ = 5,92 m.s^-2

v₁ = v₀ + 1,50.10 ^{- 4}.a₀ = 0 + 1,50.10 ^{- 4} x 5,92 = 8,90.10^-4 s

a₁ = 5,92 – 2755.v₁ = 5,92 – 2755 x 8,90.10^-4 = 3,47 m.s^-2

v₂ = v₁ + 1,50.10 ^{- 4}.a₁ = 8,90.10^-4 + 1,50.10 ^{- 4} x 3,47 = 14,1.10^-4 s

a₂ = 5,92 – 2755.v₂ = 5,92 – 2755 x 14,1.10^-4 = 2,04 m.s^-2

 

On continue ainsi les calculs jusqu'à atteindre la vitesse limite v_m .

b) On trace le graphique de v en fonction de t.

 

 

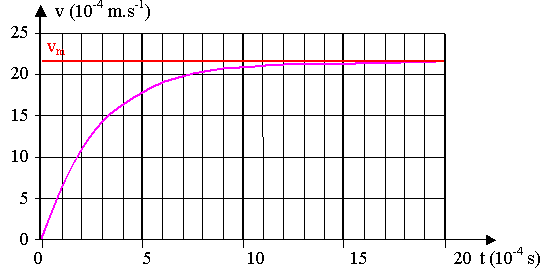
Le mouvement de la bille comporte deux phases , un régime transitoire, au cours duquel la vitesse varie  et un régime permanent pendant lequel la vitesse est constante et est égale à la valeur limite. La vitesse tend vers une valeur limite v_m = 21,5.10 ^{- 4} m.s^-1 ce qui correspond à la valeur calculée.

 

c) v = a.exp( - t / τ ) + b      ⇒     dv/dt =  - (a / τ).exp( - t / τ ) + 0

On remplace dans l'équation différentielle : - (a / τ).exp( - t / τ ) + (a / τ).exp( - t / τ ) + b/τ = k₁  soit  b/τ = k₁  ⇒  b = k₁ . τ = v_m

Pour déterminer la valeur de a , on utilise les conditions initiales :  à t = 0 s , v₀ = 0 m.s^-1 

0 = a.exp( - 0 / τ ) + b    ( exp( 0 ) = 1 )  ⇒    0 = a + b    ⇒   a = - b  

solution  :  v = - k₁ . τ exp( - t / τ ) + k₁ . τ 

v = k₁ . τ .(1 - exp ( - t / τ )) = v_m.(1 - exp ( - t / τ ))  avec τ = 3,63.10 ^{- 4} s  et v_m = 21,5.10^-4 m.s^-1

 

©Sciences Mont Blanc