Chap 13 – Mouvement d'un projectile

Etude d’un projectile

Le lancer de poids semble être l'application idéale des lois de la balistique. Le but est surtout de lancer le "poids" le plus loin possible. Ici, la poussée de l'athlète reste prépondérante et on constate que l'angle de tir est effectivement proche de 45°.

On étudie le mouvement du "poids" dans le repère orthonormé (O,,,), l'origine O étant le point du sol situé à la verticale du centre d'inertie du poids à la date t = 0 (schéma ci-dessous).

Données : pour α = 45°, sin² α = cos² α = 0,5 et tan α = 1 ; 18² = 324

Tous les calculs sont à réaliser SANS CALCULATRICE !!!

Données : si α = 45°, sin² α = cos² α = 0,5 et tan α = 1 ; 18² = 324 , g = 10 N.kg-1 , 1,8 ≈ 1,3

1) Calculer, à t = 0 s, les cordonnées du vecteur position 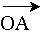et du vecteur vitesse ₀ dans le repère (O,,,) sous forme littérale.

2) Etablir sous forme littérale les équations horaires du mouvement du centre d'inertie M du "poids" dans le repère(O,,,) Montrer que le mouvement est plan.

3) En déduire l'équation littérale de la trajectoire et préciser sa nature.

4) En déduire que, pour α = 45°, le carré de la vitesse initiale peut se mettre sous la forme littérale v₀² = g.D² / (D+h), D étant la distance mesurée au sol pour ce lancer.

5) Calculer l'énergie cinétique initiale du "poids" de masse 4,0 kg ainsi lancé dans une compétition féminine, la performance étant réalisée pour un lancer D égal à 18 m et α = 45°.

6) Pour un autre lancer d'un athlète jeune, on mesure la vitesse initiale à 10 m.s^-1 et α = 45°.

Déterminer la distance D réalisée.

Solution :

1) Conditions initiales.

x₀ = 0	₀	v_0x = v₀.cos α
y₀ = OA = h = 2 m		v_0y = v₀.sin α
z₀ = 0		v_0z = 0

2) Equations horaires du mouvement.

Le système "poids" est étudié dans le référentiel terrestre galiléen auquel on associe le repère orthonormé (O,,).

Il est en chute libre, il s’est soumis qu’à son poids = m .

Deuxième loi de Newton : Dans un référentiel Galiléen, la somme des forces extérieures appliquées à un solide est égale au produit de la masse m du solide par l'accélération de son centre d'inertie : ₁ + ₂ + ₃ + …= m .

⇒ m . = m . L'accélération est donc : =

Les coordonnées du vecteur accélération sont donc :

	a_x = dv_x / dt = 0	v_x = k₁
	a_y= dv_y / dt = - g primitives ⇒	v_y = - g.t + k₂
	a_z= dv_z / dt = 0	v_z = k₃

k₁, k₂ et k₃ sont des constantes que l’on détermine en utilisant les conditions initiales

k₁ = v₀.cos α ; k₂ = v₀.sin α et k₃ = 0

	v_x = dx / dt = v₀.cos α	x = v₀.cos α.t + k₄
	v_y = dy / dt = - g.t + v₀.sin α primitives ⇒	y = - ½ g t² + v₀.sin α .t + k₅
	v_z = dz / dt = 0	z = k₆

k₄, k₅ et k₆ sont des constantes que l’on détermine en utilisant les conditions initiales

k₄ = x₀ = 0 ; k₅ = y₀ = h = 2 m ; k₆ = z₀ = 0

z = 0 à tout l’instant, la trajectoire est donc plane. Le mouvement a lieu dans un plan vertical

Les équations horaires du mouvement sont :

x = v₀.cos α .t ; y = - g.t² + v₀.sin α.t + h et z = 0

3) Etude de la trajectoire.

x = v₀.cos α .t ⇒ t = x / (v₀.cos α) .

y = - ½ g.t² + v₀.sin α .t + h = - ½ g.x² / (v₀.cos α )² + tan α.x + h

La trajectoire du "poids" est donc un arc de parabole.

4) pour α = 45°, cos α² = 0,5 et tan α = 1.

L'équation devient donc : y = - ½ g.x² / 0,5 v₀² + x + h = - g.x² / v₀² + x + h

Si x_P = D, y_P = 0 . On a donc : 0 = - g.D² / v₀² + D + h

g.D² / v₀² = D + h ⇒ v₀² = g.D² / (D+h)

5) énergie cinétique initiale du "poids" : Ec₀ = ½ m.v₀² = ½ m.g.D² / (D+h)

Ec₀ = ½ x 4,0 x 10 x 18² / (18+2) = 20 x 324 / 20 = 324 J

6) v₀ = 10 m.s^-1 , y_P = 0 = - g.D² / v₀² + D + h = - 10 D² / 100 + D + 2

0 = - 0,1 D² + D + 2 , c'est de la forme 0 = a x² + b x + c

Le discriminant est Δ = b² - 4ac = 1² + 4 x 0,1 x 2 = 1,8 ; Δ = 1,8 ≈ 1,3

Les racines sont : x₁ = (- b - Δ ) / 2a = (- 1 – 1,3) / (-0,1 x 2) = 23 / 2 = 11,5 m

x₂ = (- b + Δ ) / 2a = (- 1 + 1,3)/(-0,1 x 2) = - 3/2 = - 1,5 m