Chap 16 et 17 - Le dispositif solide-ressort

I ) Force exercée par un ressort :

Un ressort exerce une force proportionnelle à son allongement x = L - L₀ :

F = k . | L – L₀ | = k . | x | où k est le coefficient de raideur du ressort exprimé en N.m^-1 .

Si le ressort est comprimé, est vers le solide, s'il est détendu, est vers le ressort.

Expression vectorielle : On choisit un vecteur normé dans le repère Ox.

Si x < 0 , et sont dans le même sens , si x > 0 , et sont de sens contraire :  

= - k . x .

II ) Etude du système solide-ressort :

1) Oscillateur élastique libre non amorti :

Un oscillateur élastique est constitué d'un ressort fixé, reliée à un solide. C'est un oscillateur mécanique.

En l'absence de frottement, les oscillations sont libres et non amorties.

2) Etude du mouvement :

On écarte le solide de masse m de sa position d'équilibre et  on le lâche.

Le ressort a une masse supposée négligeable et un coefficient de raideur k.

On néglige tous les frottements.

O est la position du centre d'inertie du solide à l'équilibre et M sa position à un instant t.

 

Bilan des forces exercées sur le système :

:  poids du solide. P = m . g , vertical vers le bas

: force du plan sur le solide, perpendiculaire au plan vers le haut.

: force du ressort sur le solide, dans l'axe du ressort :  = - k . x .

 

On applique la 2^ème loi de Newton dans le référentiel terrestre galiléen au système de masse m. 

On associe au référentiel un repère orthonormé : O, , .

2^ème loi de Newton :             + + = m .

Projection sur l'axe (O, ) :    0 + 0 – k . x = m . x''    ( x" ou d²x/dt²)

⇒  m . x'' + k . x = 0  ⇒  x'' + (k / m) . x = 0     (équation différentielle)

 

Cette équation n'est pas à résoudre, on propose l'expression suivante :

x = x_m cos(2π t /T₀  + φ₀ )  

où T₀ est la période propre de l'oscillateur élastique et φ₀ est la phase à l'origine.

 

Cette  expression est-elle solution de l'équation différentielle du mouvement ?

* vitesse :  v(t) = dx/dt = x' = -x_m (2π/T₀) sin(2π t /T₀  + φ₀  ) ;

* accélération : a(t) = dv/dt = d²x/dt² = x'' = -x_m (4π²/T₀²) cos(2π t/T₀ + φ₀ ) = - (4π²/T₀²) . x

 

On remplace ces expressions dans l'équation différentielle :

0 = x'' + (k / m) . x = - (4π²/T₀²) x + (k / m) x

     

x n'est pas toujours nulle, on a donc :   -4π² / T₀² + k / m = 0 

T₀ = 2 π (m / k)

x = x_m cos( 2π t / T₀  + φ₀  )   est bien solution de l'équation différentielle x'' + (k / m) x = 0

avec la période propre T₀ = 2 π (m / k)  

Les oscillations libres d'un oscillateur élastique non amorti sont donc sinusoïdales.

* Vérification par analyse dimensionnelle de la dimension de 2 π (m / k)   :

[ k ] = [ F / x ] = [ m.a / x ] = M.L.T^-2 / L = M.T^-2

[2 π (m / k)] = [ m / k ]^{1 / 2} = ( M / (M.T^-2))^{1 / 2} = ( T² )^{1 / 2} = T    ( homogène à un temps)

Pour définir précisément x(t), il faut définir x_m et φ₀ en tenant compte des conditions initiales :

A t = 0 s , x = x_m cos φ₀ = x₀ . Souvent , v_x0 = 0 = - 2 π /T₀ .sin φ₀ , on a donc φ₀ = 0 ou π .

⇒ si φ₀ = 0,  x_m = x₀ ;  si φ₀ = π  , x_m = - x₀ (impossible x₀>0).  Solution : x = x₀ cos ( 2 π t / T₀ ) 

 

Remarque : Si on tient compte des forces de frottements pour les faibles vitesses : = - k'.

Elle s'oppose au déplacement. L'équation différentielle devient :    x'' + (k'/m).x' + (k/m).x = 0

III ) Oscillations libres amorties :

S'il n' y a pas de frottement, les oscillations sont sinusoïdales.

 

Si les frottements sont faibles, l’amplitude des oscillations décroît .

Le régime est pseudo-périodique. La pseudo-période T est voisine de la période propre T₀ .

 

Si les frottements sont importants, il n'y a plus d'oscillations, l'oscillateur retourne à sa position d'équilibre sans la dépasser.

Le régime est apériodique.

aucun frottement	frottements faibles	frottements importants
régime périodique	régime pseudo périodique	régime apériodique

IV ) Oscillations forcées et résonance : ( Chap 17 )

Le chapitre 15 définit les oscillations forcées. On observe ici de fortes similitudes avec le pendule.

1) Exemples :

Le haut-parleur est un exemple d'oscillations forcées. La membrane est mise en vibration par une force magnétique qui a la fréquence f du courant délivré par le générateur (GBF) qui est ici l'excitateur.     

Lire p 302 : Un pont détruit par oscillations forcées.

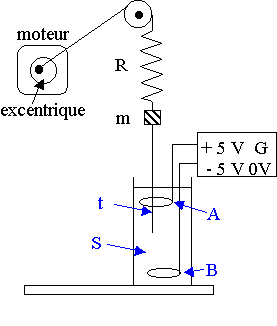2) Etude expérimentale :

 

Le résonateur étudié est l'oscillateur ressort-solide.

Le dispositif en dessous permet d'enregistrer la position de l'oscillateur grâce à une interface informatique.

Grâce à un moteur, on lui applique une force extérieure, de fréquence f égale à la fréquence de rotation du moteur.

Le résonateur oscille à la fréquence f réglable imposée par l'excitateur (moteur)..

 

On étudie les oscillations du résonateur en modifiant la fréquence f de l'excitateur .

 

On mesure l'amplitude x_m des oscillations du résonateur dans trois situations d'amortissement : faible, moyen et fort.

 

 

 

 

Si l'amortissement est faible, l'amplitude du résonateur est maximale pour une certaine fréquence f_R de l'excitateur proche de la fréquence propre f₀ du résonateur.

Il y a résonance aiguë d'amplitude.

 

Si l'amortissement est moyen, la fréquence de résonance diminue et la résonance devient plus difficile à repérer, elle est floue.

 

Si l'amortissement est grand, il n'y a plus de résonance

 

Ce phénomène de résonance s'observe pour d'autres types d'oscillations, notamment les oscillations électriques ou optiques.

 

©Sciences Mont Blanc