Chap 07 - Masse et énergie. Réactions nucléaires
I ) Equivalence masse énergie :
1) Relation d'Einstein :
En 1905, en élaborant la théorie de la relativité restreinte, Einstein postule que la masse est une des formes de l'……….. :
Un système au repos, de masse m possède une ………. de masse :
E : énergie de masse en ….. (..)
E = … … avec m : masse en …………. (…)
c : vitesse de la lumière dans le vide ( c = ……… m.s-1 )
(relation d'équivalence masse-énergie)
Conséquence : Si le système (au repos) échange de l'énergie avec le milieu extérieur, (par rayonnement ou par transfert thermique par exemple), sa variation d'énergie DE et sa variation de masse Dm sont liées par la relation : DE = …………..
Ø Si Dm < 0 alors DE .. 0, le système …… de l'énergie au milieu extérieur et sa masse ……….
Ø Si Dm > 0 alors DE .. 0, le système ……. de l'énergie du milieu extérieur et sa masse ………..
2) Unités :
A l'échelle atomique, l'unité joule est inadaptée , trop grande ; on utilise plutôt l'électron volt , eV : 1 eV= 1,60.10-19 J et aussi le MeV: 1 MeV = 106 eV = 1,60.10-13 J.
exemple : Déterminer l'énergie de masse E d'un proton en J et en MeV : ( mp = 1,67.10-27 kg )
E = .......... = ……..x (…………) » ………… J » …… MeV
Remarque : A cette échelle, l'unité kg est aussi inadaptée,
on utilise parfois l'unité de masse atomique notée u . Elle est égale au douzième
de la masse d'un atome de carbone ![]() .
.
1 u =…….. / ( …. …. ) = …………………….. = …………… kg
II ) Energie de liaison du noyau :
1) Défaut de masse du noyau :
On a constaté en mesurant les masses que la masse du noyau atomique est ………… à la somme des masses des protons mp et des neutrons mn qui le constituent : mnoyau … Z.mp + (A-Z).mn
Cette différence est appelée défaut de masse Dm : Dm = ……………………………..( Dm … 0 )
Exemple: Calculer Dm pour un noyau d'hélium :
données : mn=1,67496.10-27
kg , mp = 1,67265.10-27 kg et m(![]() ) =6,6447.10-27
kg
) =6,6447.10-27
kg
Dm = ……………………………..= ……………………………………. = ………….. kg
2) Energie de liaison du noyau :
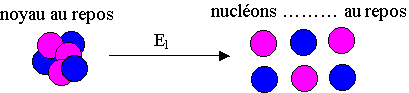 Définition:
On appelle énergie de liaison d'un noyau , notée El , l'énergie
que le milieu extérieur doit ………. à un noyau au repos pour le ……….. en nucléons
……….. au repos.
Définition:
On appelle énergie de liaison d'un noyau , notée El , l'énergie
que le milieu extérieur doit ………. à un noyau au repos pour le ……….. en nucléons
……….. au repos.
Lorsque le noyau se …………, la masse …………. de Dm et l'énergie de Dm.c2.
L'énergie de liaison d'un noyau a pour expression :
El : énergie de liaison du noyau (en J) à convertir en MeV
El = ……….. avec Dm : défaut de masse du noyau (en kg)
c : célérité de la lumière dans le vide (en m.s-1)
Pour un noyau d'hélium : El = ………= …………………… = ……….. J = …….. MeV
Remarque: Inversement, lorsque le noyau se forme à partir de ses nucléons libres, le milieu extérieur ……….. l'énergie E= ………. (la masse du système ………. et Dm…0).
3) Energie de liaison par nucléon :
Définition: L'énergie de liaison par nucléon d'un noyau notée EA est le quotient de son énergie de liaison par le nombre de ses ………..
EA: énergie de liaison par nucléon (en Mev/nucléon)
EA = ……….. avec El: énergie de liaison du noyau (en Mev)
A: nombre de nucléons du noyau
Pour un noyau d'hélium : EA = ………= ……….. = ……. MeV
Remarque: EA permet de comparer la ……….des
noyaux entre eux.
Plus l'énergie de liaison par nucléon est grande, plus le noyau est ……….
 4)
Courbe d'Aston :
4)
Courbe d'Aston :
La courbe d'Aston représente ………en fonction de …(nombre de ……….).
Elle permet de visualiser facilement les noyaux les plus stables ,ceux-ci se trouvent au …. du graphe comme le noyau de …..
( A entre 20 et 195)
Les noyaux instables peuvent évoluer de 2 façons :
Ø Les noyaux lourds peuvent se ……… en 2 noyaux ……. appartenant au domaine de stabilité. C'est la ………...
Ø 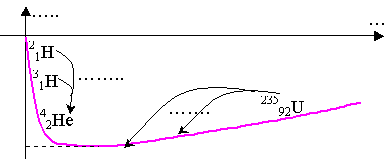 Certains
noyaux ……… peuvent "………….." pour former un noyau plus …… et stable.
Certains
noyaux ……… peuvent "………….." pour former un noyau plus …… et stable.
C'est la ……...
III ) Fission et fusion nucléaires :
1) Réactions nucléaires provoquées :
Définition: Une réaction nucléaire est dite provoquée lorsqu'un noyau ……est frappé par un noyau ………. et donne naissance à de …………. noyaux.
Les lois de conservation de Soddy sont………..
Exemple : Expérience de Rutherford en 1919 : le bombardement de noyaux d'azote avec des particules a provoque la formation de noyaux d'………… et de ………...
2) La fission nucléaire: réaction en chaîne :
Définition: La fission est une réaction nucléaire provoquée au cours de laquelle un noyau ……. "…….." donne naissance à deux noyaux plus ………..
Exemple: Plusieurs réactions de fission de l'uranium 235 sont possibles:
![]() +
+
![]() ® ……. + ……. +..
® ……. + ……. +.. ![]()
![]() +
+
![]() ® ……. + ……..+..
® ……. + ……..+.. ![]()

![]() +
+
![]() ® ..... + .... +..
® ..... + .... +.. ![]()
Les neutrons émis lors de la fission peuvent provoquer la
………d'autres noyaux. Si le nombre de neutrons émis lors de chaque fission est
……….. à 1, une réaction en …….. peut se produire et devenir rapidement …………(bombe
à fission : bombe "A" d'Hiroshima).
Dans une centrale nucléaire, la réaction en chaîne est …………. par des barres
mobiles qui plongent dans le réacteur entre les barres de "combustible"
pour ……….. une partie des neutrons émis. On peut ainsi contrôlé la ………… d'énergie
produite par les réactions de fission.
Pour amorcer une fission, il faut ……….. une quantité minimale d'énergie au système.
3) La fusion nucléaire :
Définition:
La fusion nucléaire est une ……….. de deux noyaux ………. pour former un noyau plus ……..

Equation : ![]() +
+ ![]() ®…….+
®…….+![]()
L'énergie libérée au cours d'une fusion est considérable.
La fusion n'est possible que si les deux noyaux possèdent une grande ……….. ………..pour vaincre les forces de répulsion électriques.
La fusion se produit naturellement dans les étoiles.
Dans une bombe thermonucléaire (appelée bombe H), la fusion nucléaire est incontrôlée et explosive
Elle est très intéressante pour produire de l'énergie , mais on ne la maîtrise pas suffisamment pour produire de l'électricité .
IV ) Bilan énergétique :
1) Cas général :
Equation d'une réaction nucléaire : ![]() +
+ ![]() ®
®![]() +
+![]()
D'après l'équivalence masse-énergie, la variation d'énergie DE de la réaction correspond à la variation de masse Dm : Dm = ……………………DE = ……….
Remarque : DE =………………… ( voir définition de El)
2) Réactions nucléaires spontanées :
Radioactivité a :
![]() ®
® ![]() +
+
![]()
Energie fournie au milieu extérieur : DE = [m(…..) + m(……..) - m(……)].c2
Exemple : désintégration a d'un noyau de radium 226 en noyau de radon 222
m(![]() )=225,9770 u, m(
)=225,9770 u, m(![]() )=221,9702
u, m(
)=221,9702
u, m(![]() )
= 4,0015 u, ( 1 u = 931,5 MeV/c2 )
)
= 4,0015 u, ( 1 u = 931,5 MeV/c2 )
![]() ®
®![]() +
+![]() DE = [m(…..)
+ m(…..) - m(….)].c2
DE = [m(…..)
+ m(…..) - m(….)].c2
DE = ………………………………= …. MeV
Désintégration b-
: ![]() ®
® ![]() +
+![]() DE = [m(….) + m(…..) - m(….)].c2
DE = [m(….) + m(…..) - m(….)].c2
Exemple : désintégration b- du cobalt 60 en nickel 60
m(![]() )
= 59,9190 u , m(
)
= 59,9190 u , m(![]() )
= 59,9154 u , m(
)
= 59,9154 u , m(![]() )
= 5,49.10-4 u
)
= 5,49.10-4 u
![]() ®
® ![]() +
+
![]() DE = [m(…..)
+ m(….) - m(….)].c2
DE = [m(…..)
+ m(….) - m(….)].c2
DE = ………………………… = ………. MeV
3) Réactions de fission et de fusion :
Pou la fission, étudions la réaction utilisée par une centrale nucléaire : la fission de l'uranium 235.
![]() +
+
![]() ® …… + …….+ …
® …… + …….+ … ![]()
remarque : La fission d'un noyau d'uranium peut donner d'autres noyaux fils.
m(![]() )
= 234,9935 u ; m(
)
= 234,9935 u ; m(![]() )
= 93,8945 u ; mn = 1,0087 u; m(
)
= 93,8945 u ; mn = 1,0087 u; m(![]() )
= 139,8920 u
)
= 139,8920 u
DE = [m(….) + m(.....) + ...mn - m(......) - mn ].c2
DE = …………………………….. = ………… MeV
Cette énergie est énorme par rapport à la combustion de pétrole .
1 kg d'uranium fournit autant d'énergie que 2 000 Tonnes de pétrole.
Pour la fusion, prenons l'exemple de la fusion de 2 noyaux d'hélium 3
![]() +
+ ![]() ®
® ![]() + ..
+ ..![]()
m(![]() )
= 3,0149 u ; m(
)
= 3,0149 u ; m(![]() )
= 4,0015 u ; mp = 1,0073 u
)
= 4,0015 u ; mp = 1,0073 u
DE = [m(…..)+...mp- …m(……)].c2=………………………………………. = ……. MeV.
Remarque : Par nucléon, la fusion libère plus d'énergie que la fission.
©Sciences Mont Blanc