Sujet Bac Antilles Septembre 2003

Calculatrice autorisée

 

I ) Espèces acides en solution (6,5 points)

II ) Défibrillateur cardiaque (5,5 points)

III ) L'âge de la Terre (4 points)

III ) (spe) Emission et réception d'une onde modulée en amplitude (4 points)

 

Antilles Septembre 2003 - I ) Espèces acides en solution :

On se propose d’identifier deux espèces chimiques acides différentes notées HA₁ et HA₂ , en utilisant quelques mesures mettant en jeu différentes techniques expérimentales.

Tout d’abord, on prépare les deux solutions aqueuses S₁ et S₂, à partir des espèces HA₁ et HA₂ et d’eau distillée , de telle manière que la concentration en soluté apporté soit C₀ = 1,0.10^-2 mol.L^-1  pour chacune d’elles. On considère que la réaction de chaque espèce acide dans l’eau est instantanée.

Les parties I, II et III sont indépendantes.

I ) Mesure par pH-métrie :

1) Nous allons tenter de différencier ces deux espèces acides en observant leur action sur l’eau, par l’intermédiaire d’une mesure de pH réalisée dans les m^mes conditions pour chaque solution.

a) Définir une espèce acide selon Brönsted.

b) Ecrire l’équation qui représente la réaction d’une espèce acide quelconque HA avec l’eau.

Indiquer les deux couples acide/base mise en jeu à cette occasion.

c) On néglige toute autre réaction. Quelle relation a-t-on, dans ces conditions, entre les quantités de matière de A^- et H₃O⁺ ?

2) On réalise la mesure du pH, à 25°C, en utilisant un volume V = 200 mL de chacune des deux solutions S₁ et S₂ . Des mesures précises de pH pour S₁ et S₂ permettent de calculer leurs concentrations effectives en ions oxonium :

         [H₃O⁺]₁ = 1,3.10^-3 mol.L^-1  pour S₁       et     [H₃O⁺]₂ = 1,0.10^-2 mol.L^-1  pour S₂

a) Calculer les quantités de matière en ions oxonium, n(H₃O⁺ )₁ et n(H₃O⁺)₂ dans chaque solution.

b) Calculer la quantité de matière d’acide HA₁ et HA₂ , initialement présente dans les 200 mL de chaque solution avant toute réaction avec l’eau.

c) Exprimer l’avancement maximal de la réaction et calculer sa valeur en fonction des données.

- Calculer l’avancement final x_f1 et x_f2 pour la réaction de chaque acide avec l’eau.

- Préciser la signification du taux d’avancement final et calculer t₁ et t₂ pour chaque réaction.

II ) Suivi spectrophotométrique :

L’une des deux réactions précédentes se caractérise par un taux d’avancement final maximal. Pour identifier précisement l’espèce acide qui participe à cette réaction, on introduit dans les 200 mL de cette solution 4 mL d’une solution de peroxyde d’hydrogène (H₂O₂ ), de concentration

C = 0,10 mol.L^-1 . On observe alors l’apparition d’une coloration jaune très pâle qui se renforce progressivement ; cette coloration est caractéristique du diiode en solution aqueuse.

La transformation d’oxydoréduction qui se déroule alors peut être décrite par l’équation suivante :

H₂O_{2 (aq)} + 2 H₃O⁺_(aq) + 2 I^-_(aq) = 4 H₂O_(l) + I_{2 (aq)}

 

 

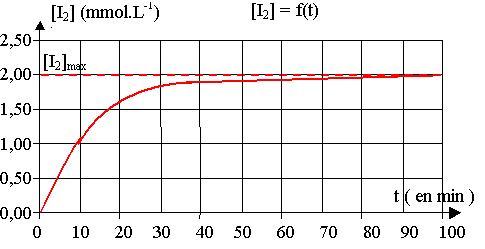
1) Par spectrophotométrie, on établit la courbe qui représente l’évolution de la concentration en diiode formé au cours du temps (courbe ci-après), ce qui permet de suivre le déroulement de la réaction.

a) Tracer les tangentes à la courbe aux points d’abscisse : t= 0 min ; t = 20 min ; t = 60 min.

b) Indiquer comment varie la vitesse de réaction au cours du temps. Justifier cette évolution.

c) A quelle date la vitesse de réaction est-elle maximale ?

d) Donner la définition du temps de demi-réaction t_1/2 .

e) Faire sa détermination graphique sur la courbe donnée ci-avant et indiquer sa valeur.

2) La réaction (1) représente une transformation d’oxydoréduction :

a) Identifier les deux couples oxydant/réducteur mis en jeu dans cette équation.

b) Ecrire les demi-équations correspondantes.

c) Quelle est l’espèce chimique qui subit une oxydation ?

d) identifier l’espèce acide recherchée HA en donnant sa formule.

III ) Mesure conductimétrique :

Pour identifier à présent l’autre acide, on réalise une mesure de conductivité de sa solution ; on immerge la cellule du conductimètre dans les 200 mL de solution utilisée au I. 2) ; on obtient s_exp. = 53,4 mS.m^-1 .

La conductivité d’une solution est liée à la concentration effective des espèces chargées en solution par la relation suivante :

s = ( l_x+.[X⁺] + l_y-.[Y^-])

 mS.m^-1                mS.m².mol^-1       mol.m³

(pour une solution contenant les ions X⁺ et Y^- )

 

1) Exprimer cette relation pour la solution acide étudiée, en considérant uniquement les ions formés après réaction de l’el(A^-) = (s / [H₃O⁺] ) - l(H₃O⁺) = (53,4 / 1,3 ) – 35,0 = 6,1 mS.m².mol^-1 spèce acide avec l’eau.

2) En utilisant le résultat du I.1.c), exprimer la conductivité molaire ionique l(A^-) de la base conjuguée de l’espèce acide, en fonction des autres grandeurs, s , l(H₃O⁺), [H₃O⁺].

Calculer sa valeur (utiliser les valeurs données en I.2) ).

3) En considérant les valeurs de conductivités molaires ioniques du tableau ci-dessous, identifier la nature de la base conjuguée présente en solution.

Donner la formule du deuxième acide recherché.

 

 

©Sciences Mont Blanc

 

 

 

Antilles Septembre 2003 - II ) Défibrillateur cardiaque :

 

 

       

 

©Sciences Mont Blanc

 

 

 

Antilles Septembre 2003 - III ) L'âge de la Terre:

 

La détermination de l'âge de la Terre a commencé vers le XVIe siècle, on l'estimait alors autour de 5 000 ans. Au XIXe siècle, des scientifiques admettaient un âge d'environ 100 millions d'années.

La découverte de la radioactivité, par H. Becquerel en 1896, bouleversa toutes les données connues. La datation à l'uranium-plomb permit de déterminer assez précisément l'âge de la Terre.

Nous proposons de comprendre cette technique de datation.

I ) Etude de la famille Uranium – Plomb 206 :

Le noyau d'uranium 238, naturellement radioactif, se transforme en un noyau de plomb 206, stable, par une série de désintégrations successives. Nous allons étudier ce processus.

(On ne tiendra pas compte de l'émission g.)

1) Dans la première étape, un noyau d'uranium  subit une radioactivité a . Le noyau-fils est du thorium (symbole Th).

a) Qu'est-ce qu'un noyau radioactif ?

b) Ecrire l'équation de la réaction nucléaire en précisant les règles utilisées.

2) Dans la deuxième étape, le noyau de thorium 234 se transforme en un noyau de protactinium . 

L'équation de la réaction nucléaire est :   ®  +

Préciser, en justifiant, le type de radioactivité correspondant à cette transformation.

3) L'équation globale du processus de transformation d'un noyau d'uranium 238 en un noyau de plomb 206 est :

 ®  + 8  + 6

Déterminer, en justifiant, le nombre de désintégrations a et b^- de ce processus.

II ) Géochronologie :

On a constaté, d'une part, que les minéraux d'une même couche géologique, donc du même âge, contiennent de l'uranium 238 et du plomb 206 en proportions remarquablement constantes et, d'autre part, que la quantité de plomb dans un minéral augmente proportionnellement à son âge relatif.

Si on mesure la quantité de plomb 206 dans un échantillon de roche ancienne, en considérant qu'il n'y en avait pas initialement, on peut déterminer l'âge du minéral à partir de la courbe de décroissance radioactive du nombre de noyaux d'uranium 238.

Etudions un échantillon de roche ancienne dont l'âge, noté t_Terre , correspond à celui de la Terre.

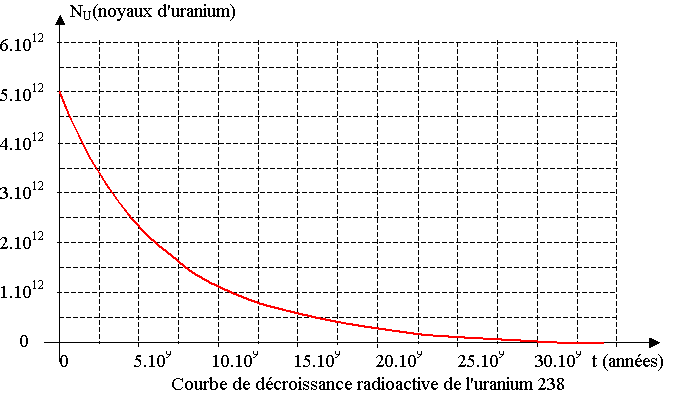
1) On considère la courbe de décroissance radioactive du nombre N_U( t) de noyaux d'uranium 238 dans un échantillon de roche ancienne, voir l'annexe (à rendre avec la copie).

a) Indiquer la quantité initiale N_U(0) de noyaux d'uranium.

b) Déterminer graphiquement la valeur de la constante de temps t de l'uranium 238 (représenter la construction sur la courbe de l'annexe). En déduire la valeur de sa constante de radioactivité l.

c) Donner l'expression de N_U(t) , nombre de noyaux radioactifs présents dans l'échantillon à la date t, en fonction de N_U(0).

Calculer le nombre de noyaux d'uranium 238 qui restent dans la roche à la date t₁ = 1,5.10⁹ ans. Vérifier graphiquement votre résultat.

d) Définir et déterminer graphiquement le temps de demi-vie t_1/2 de l'uranium 238 (représenter la construction sur la courbe de l'annexe).

2) La quantité de plomb mesurée dans la roche à la date t_Terre ,notée N_Pb(t_Terre) , est égale à

2,5.10¹² atomes.

a) Etablir la relation entre N_U(t_Terre) , N_U(0) et N_Pb(t_Terre) . Calculer la quantité N_U(t_Terre) de noyaux d'uranium.

b) Déterminer l'âge t_Terre de la Terre.

 

Annexe (à rendre avec la copie)

 

 

 

 

©Sciences Mont Blanc

 

 

 

Antilles Septembre 2003 - III ) (spe) Emission et réception d'une onde modulée en amplitude :

 

On s'intéressera aux stations de la bande des grandes ondes pour lesquelles toutes les porteuses sont modulées en amplitude par des signaux audio-fréquences (ondes dont la fréquence est comprise entre 20 Hz et 20 000 Hz).

1 ) Emission d'une onde modulée en amplitude :

1.1) Etude de l'onde porteuse :

Pour simuler l'onde porteuse, on utilise un GBF délivrant une tension sinusoïdale p(t) d'amplitude P_m et de fréquence f_P. Cette tension a pour expression :  p(t) = P_m . cos(2 p . f_P . t)

On visualise cette tension à l'aide d'un oscilloscope. L'oscillogramme obtenu est le suivant.

 

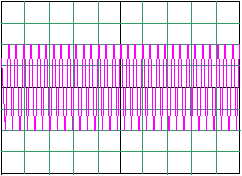
Figure 1 : Oscillogramme 1.

Coefficient de balayage : 20 ms /div

Sensibilité verticale : 1 V / div

Couplage : DC

 

En l'absence de tension, le spot occupe la ligne médiane de l'écran.

 

 

1.1.1) D'après l'oscillogramme 1, déterminer l'amplitude P_m de la tension sinusoïdale p(t) représentée.

1.1.2) D'après l'oscillogramme 1, déterminer la période T_P de la tension p(t) ; comment peut-on obtenir la meilleure précision sur la détermination de la période en maintenant le coefficient de balayage constant ?

1.1.3) En déduire la fréquence de la tension p(t).

1.14) Déterminer la longueur d'onde l d'une onde porteuse ayant la même fréquence que la tension sinusoïdale p(t).

Donnée : la célérité des ondes électromagnétiques dans l'air  c = 3,0.10⁸ m.s^-1 

 

1.2) Etude du signal modulant :

Pour simuler le signal modulant, on utilise un GBF délivrant une tension sinusoïdale s(t) d'amplitude S_m et de fréquence

f_S = 10 kHz.

Cette tension a pour expression : s(t) = S_m . cos ( 2p . f_S . t). 

A l'aide du réglage du décalage du signal de sortie du générateur, on superpose à la tension sinusoïdale s(t) une tension constante positive, de valeur U₀.

On visualise la tension s(t) + U₀ à l'aide d'un oscilloscope.

 

 

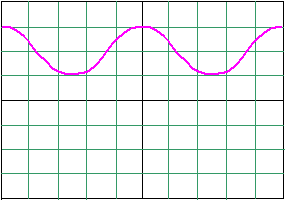
Figure 2 : Oscillogramme 2.

Coefficient de balayage : 20 ms /div

Sensibilité verticale : 1 V / div

Couplage : DC

 

En l'absence de tension, le spot occupe la ligne médiane de l'écran.

 

 

1.2.1) L'oscillogramme obtenu est représenté sur la figure 2.

Déterminer l'amplitude de la tension modulante S_m.

1.2.2) Sur l'oscillogramme 2, déterminer la tension de décalage U₀.

 

1.3) Etude de la réalisation d'une onde modulée en amplitude

La modulation en amplitude est réalisée à l'aide d'un multiplieur. Son rôle est ainsi défini :

On applique entre la masse et chacune des entrées E₁ et E₂ du multiplieur une tension électrique :

         - la tension sinusoïdale p(t) sur E₁ qui correspond à la porteuse.

         - la tension sinusoïdale s(t) + U₀ sur E₂ qui correspond au signal modulant à transmettre.

Le multiplieur donne en sortie une tension u(t) qui correspond au signal modulé.

Cette tension a pour expression : u(t) = k . p(t) . (s(t) + U₀), avec p(t) = P_m . cos(2p . f_P . t)

                                                                                                 s(t) = S_m . cos(2p . f_S . t)

et k constante caractéristique du multiplieur.

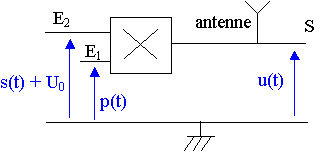
En S, on place une antenne qui émet l'onde modulée en amplitude.

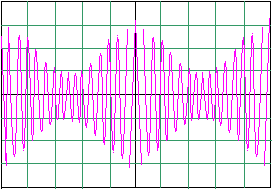
On visualise la tension u(t) à l'aide d'un oscilloscope. L'oscillogramme obtenu est représenté sur la figure 3.

 

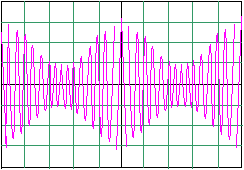
Figure 3 : Oscillogramme 3.

Coefficient de balayage : 20 ms /div

Sensibilité verticale : 1 V / div

 

Couplage : DC

En l'absence de tension, le spot occupe la ligne médiane de l'écran.

 

1.3.1) En introduisant le taux de modulation m = S_m / U₀ et en posant A = k . P_m . U₀ , montrer que la tension modulée en amplitude peut se mettre sous la forme :

               u(t) = A . ( m . cos(2p . f_S . t) + 1) . cos(2 p . f_P . t)

1.3.2) Une tension modulée en amplitude peut également se mettre sous la forme :

               u(t) = U_m(t) . cos(2 p . f_P . t)    avec   U_m(t) =  A . ( m . cos(2p . f_S . t) + 1)

L'amplitude de la tension modulée U_m(t) varie entre deux valeurs extrêmes, notées U_min et U_max,

Ø      Déterminer les expressions littérales de U_min et U_max en fonction de A et m.

Ø      En déduire que l'expression littérale du taux de modulation peut se mettre sous la forme :

               m = (U_max – U_min) / (U_max + U_min)

1.3.3) Sur l'oscillogramme de la figure 3, déterminer les valeurs de U_max et U_min et calculer la valeur du taux de modulation m.

La comparer avec la valeur trouvée en utilisant l'expression m = S_m / U₀ .

1.3.4) Citer la condition pour éviter la surmodulation.

Les résultats précédents permettent-ils d'affirmer que cette condition est vérifiée ?

2 ) Réception de l'onde modulée

Pour capter l'onde électromagnétique émise par l'antenne placée en S, on utilise le dispositif représenté ci-dessous (figure 4) où on considère que la diode D est idéale. Il s'agit d'un récepteur d'ondes hertziennes, qui constitue une chaîne électronique dont on va étudier certains étages.

 

 

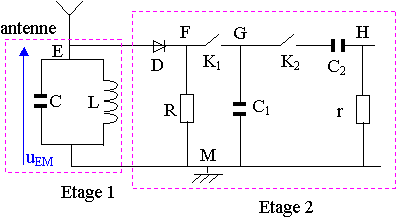
2.1) L'étage 1 étudié est un circuit constitué par une association condensateur – bobine en parallèle.

2.1.1) Quel est le rôle du dipôle LC parallèle utilisé ici comme filtre passe-bande pour la tension ?

2.1.2) La théorie montre que l'amplitude de la tension u_EM est maximale pour une fréquence de l'onde captée f₀ telle que

4p² . f₀² . L . C = 1 . Sachant que la valeur de la capacité C est 0,47 nF, déterminer la valeur à donner à l'inductance L de la bobine pour capter France Inter grandes ondes (fréquence de la station : 160 kHz). La réception de l'onde émise sera alors optimale.

 

2.2) Après réception du signal modulé, il faut le démoduler.

Cette démodulation est réalisé par l'étage 2.

Pour comprendre les rôles de chaque partie de cet étage, on va les étudier à l'oscilloscope. On relie donc successivement l'entrée de l'oscilloscope aux bornes E, G et H du montage ci-dessus.

On visualise successivement les trois tensions u_EM, u_GM et u_HM sur un oscilloscope, M étant la masse du circuit. Les oscillogrammes des trois tensions sont obtenus en utilisant le mode DC de l'oscilloscope.

 

 Oscillogramme A                                    Oscillogramme B

 

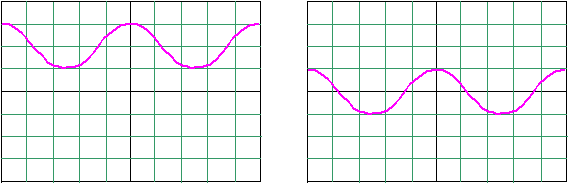
Oscillogramme C

 

En l'absence de signal appliqué aux voies, les traces obtenues sur l'écran coïncident avec la ligne horizontale médiane.

2.2.1) Les deux interrupteurs K₁ et K₂ étant ouverts, identifier u_EM en indiquant l'oscillogramme A  B ou C correspondant. Justifier.

2.2.2) K₁ étant fermé et K₂ étant ouvert, identifier u_GM en indiquant l'oscillogramme A, B ou C correspondant. Quel est le rôle de l'ensemble diode D et circuit RC₁ parallèle ?

2.2.3) K₁ et K₂ étant fermés, identifier u_GM en indiquant l'oscillogramme A, B ou C correspondant. Quel est le rôle du dipôle rC₁ série utilisé ici comme filtre passe-haut ?

2.2.4) On souhaite obtenir une démodulation de bonne qualité en choisissant la valeur de la capacité C₁ adaptée. La constante de temps RC₁ doit alors satisfaire aux conditions suivantes :

RC₁ < T_S  avec T_S période du signal modulant.

RC₁ > T_S  avec T_P période de la porteuse.

Application : la période T_S du signal sonore à transporter est égale à 100 ms, et la période T_P de la porteuse est égale à 6,25 ms. Le conducteur ohmique a une résistance R = 10 kW.

Déterminer alors, dans la liste suivante, la valeur de la capacité C₁ permettant d'obtenir la meilleure démodulation possible.

Liste des valeurs des capacités disponibles : 220 pF – 2,2 nF – 22 nF – 220 nF.

 

 

©Sciences Mont Blanc