Sujet Bac Antilles Juin 2004

Calculatrice autorisée

 

I ) Brouillard et vitesse ( 9,5 points)

II ) Durée de fonctionnement d'une pile cuivre-aluminium ( 2,5 points)

III ) Contrôle de qualité sur l'aspirine de laboratoire ( 4 points)

III (spe) Dosage du glucose libre d'un jus de fruit ( 4 points)

 

Antilles Juin 2004 - I ) Brouillard et vitesse :

Le brouillard est un phénomène qui réduit la visibilité à quelques dizaines de mètres.

Il se compose de très fines gouttelettes d’eau.

Les brouillards se forment lorsque l’air humide rencontre une zone froide. L’air devient alors saturé en vapeur d’eau et celle-ci se condense pour former de très petites gouttelettes en suspension dans l’air. C’est le même principe qui est à la base de la formation des nuages.

Le brouillard est une forme de nuage qui touche le sol.

I ) Modèle simple :

Les gouttelettes qui se forment lors de cette condensation au voisinage du sol sont de très petites dimensions (indiscernables à l’œil nu) ; nous allons considérer l’évolution d’une goutte de brouillard sphérique, de rayon r, de masse m, située à une altitude h par rapport au sol et soumise au seul champ de pesanteur terrestre.

On suppose la goutte immobile au début de l’étude, et on oriente l’espace par un axe vertical descendant, repéré (Oz), dont l’origine est la position occupée par la goutte à cet instant initial.

Données :    g = 9,8 N.kg^–1       volume du sphère : V = 4/3 p.r³                   r_eau = 1,0.10³ kg.m^–3

1) Quelle propriété présente le champ de pesanteur terrestre dans un volume comparable à celui d’une nappe de brouillard ? (ordre de grandeur : le km³)

2) Nommer et énoncer la loi qui, appliquée au centre d’inertie de la goutte, permet d’exprimer son vecteur accélération.

3) Etablir l’équation horaire du centre d’inertie de la goutte de brouillard dans ces conditions.

4) Calculer la vitesse de la goutte quand elle atteint le sol, en prenant h = 10 m.

II ) Frottements :

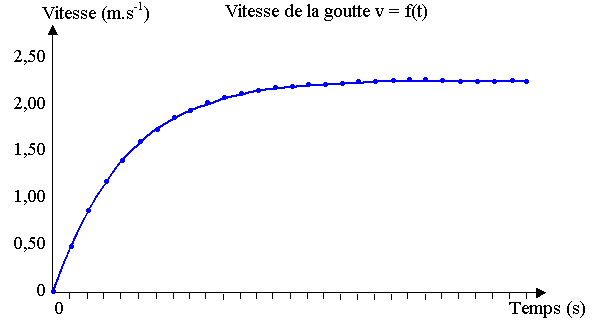
En réalité, une observation minutieuse du brouillard à proximité du sol permet d'estimer la vitesse constante de ses gouttelettes; on obtient: v_L = 2,30.10^–2 m.s^–1

Pour nous rapprocher des conditions réelles, envisageons d'autres forces agissant sur la goutte de brouillard.

1) Donner l'expression de la poussée d’Archimède s'exerçant sur cette goutte en fonction de r_air, de V_g (volume de la goutte) et de g, la masse volumique de l'air étant r_air = 1,3 kg.m^–3.

2) Exprimer le poids de la goutte de brouillard en fonction de r_eau, de V_g et de g et comparer cette expression à celle obtenue à la question précédente. Conclure.

3) On envisage l'existence d'une force de frottement fluide exercée par l'air sur la goutte pendant son déplacement, elle est exprimée sous la forme:  F = – k. v

a) Etablir alors l'équation différentielle à laquelle obéit le centre d'inertie de la goutte de brouillard, dans son mouvement selon l’axe Oz, et la mettre sous la forme :

         dv/dt = a.v + b      (1)

b) Identifier les constantes a et b et les exprimer en fonction des données de l'énoncé.

c) Exprimer la vitesse limite atteinte par la goutte, v_L, à partir de l'équation différentielle précédente dans le cas où l'accélération du centre d'inertie de la goutte s'annule, en fonction de m, g et k.

d) En utilisant l'expression obtenue, rechercher par analyse dimensionnelle, l'unité du coefficient k qui intervient dans l’expression de la force de frottement.

III ) Brouillard simulé :

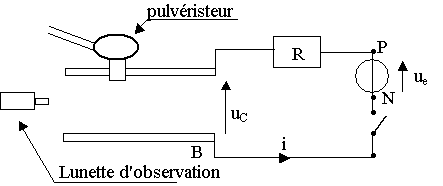
Pour en savoir un peu plus à propos du brouillard, on utilise le dispositif suivant: une lunette permet d'observer finement une zone située entre les deux armatures horizontales A et B d'un condensateur plan ; l'armature supérieure est percée d'un orifice qui permet à l'opérateur de pulvériser un brouillard de fines gouttelettes entre les deux armatures.

Le générateur délivre une tension positive constante de valeur U_e entre ses bornes P et N.

La valeur de la résistance est R ; on note u_C la tension aux bornes du condensateur et u_R celle aux bornes du résistor;

1) On ferme l'interrupteur à t = 0.

a) Sur le schéma de l'annexe 1, indiquer le signe de la charge qui apparaît sur chaque armature pour t > 0.

b) En considérant l'orientation choisie pour i, écrire la relation qui existe entre l'intensité du courant i(t) et la charge acquise, notée q, par l'armature positive du condensateur.

c) La charge acquise par le condensateur est à tout moment proportionnelle à u_C :

q(t) = C .u_C(t). En exploitant cette relation, établir l'expression liant i(t) à u_C(t).

d) En déduire l'équation différentielle (2) à laquelle obéit la tension u_C(t).

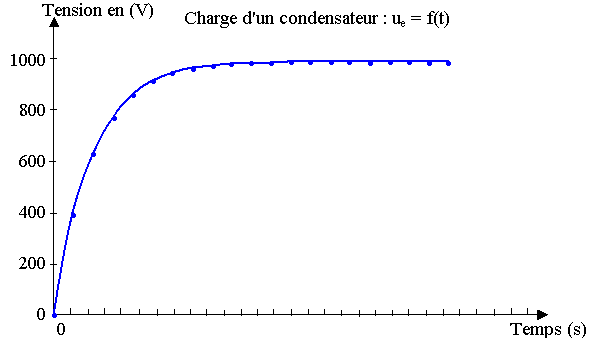
2) La solution analytique de l'équation différentielle (2) prend la forme: u_C(t) = U_e.(1 – e ^{–t / R.C}).

Vérifier que cette solution satisfait à l'équation différentielle (2).

IV ) Analogie mécanique-électrique

On constate que l'évolution temporelle du système électrique «condensateur» est analogue à celle du système mécanique «goutte de brouillard». En effet, l'équation différentielle (1) peut également être résolue analytiquement; elle conduit alors à la solution suivante :

v(t) = v_L . (1 – e ^{–k.t / m})

1) Identifier, parmi les propositions suivantes, en s'appuyant sur l'allure des courbes v = f(t) et     u_C = f(t) données en annexe 2, le régime d'évolution commun aux deux systèmes étudiés.

a) régime divergent : la valeur de la grandeur physique étudiée tend à augmenter (en valeur absolue) au cours du temps.

b) régime convergent: la valeur de la grandeur physique étudiée tend vers une valeur limite constante; l'évolution du système présente alors deux phases distinctes: un régime transitoire et un régime établi ou permanent.

c) régime périodique: la valeur de la grandeur physique étudiée se répète de manière identique à intervalles de temps égaux.

2) Rappeler l'expression de la constante de temps t pour un circuit RC et réécrire l'expression de u_C(t) en fonction de t.

3) En comparant les expressions de v(t) et u_C(t), identifier et donner l'expression de la constante de temps pour le système de la goutte de brouillard.

V ) Brouillard stabilisé :

Lorsque la tension aux bornes du condensateur est U_e, toute particule porteuse d'une charge électrique q, est soumise à une force électrique, , de direction perpendiculaire aux armatures vérifiant l'expression       F_e= ½q ½.U_e / d ,   « d » étant la distance séparant les 2 armatures A et B.

On pulvérise à présent entre les plaques du condensateur un brouillard de fines gouttelettes.

Au cours de cette opération celles-ci acquièrent, par frottement, une charge électrique « q » négative. La lunette permet d'observer les gouttelettes dans leur mouvement de chute.

Pour une tension U_e = 1,0.10³ V, il est possible de les immobiliser.

1) Montrer que dans ces conditions les seules forces à prendre en compte sont le poids et la force électrique.

2) A l'aide de la première loi de Newton, écrire la relation vectorielle entre ces deux forces et les représenter sur le schéma de l'annexe 1.

3) Etablir l’expression littérale de la valeur absolue de la charge ½q½.

En déduire sa valeur, sachant que d = 0,10 m et que le micromètre intégré à la lunette a permis de déterminer le rayon moyen des gouttelettes, soit r = 5,4.10^–6 m.

On rappelle les données de l'énoncé :

g = 9,8 N.kg^–1                volume du sphère : V = 4/3 p . r³                 r_eau = 1,0.10³ kg.m^–3

4) D'après le sens de la force électrique, déterminer le signe des charges Q_A et Q_B portées par les armatures A et B du condensateur. Ce résultat est-il cohérent avec celui de la question 3 ?

Annexe 1 A rendre avec la copie

Schéma à compléter :

 

 

 

©Sciences Mont Blanc

 

 

 

Antilles Juin 2004 - II ) Durée de fonctionnement d'une pile cuivre-aluminium :

 

Une pile est composée de deux demi-piles reliées par un pont salin (papier filtre imbibé d’une solution de chlorure de potassium).

La première demi-pile est constituée d’une lame d’aluminium de masse m₁ = 1,0 g qui plonge dans 50 mL de solution de sulfate d’aluminium (2Al³⁺_(aq) + 3SO₄^2-_(aq)) de concentration en ion aluminium [Al³⁺_(aq)] = 5,0.10^-1 mol.L^-1. La seconde est constituée d’une lame de cuivre de masse m₂ = 8,9 g qui plonge dans 50 mL de solution de sulfate de cuivre (Cu²⁺_(aq) + SO₄^2-_(aq)) de concentration [Cu²⁺_(aq)] = 5,0.10^-1 mol.L^-1.

On associe à cette pile un ampèremètre et une résistance en série.

 

1) Réaliser le schéma annoté de la pile.

2) L’ampèremètre indique que le courant circule de la plaque de cuivre vers la plaque d’aluminium à l’extérieur de la pile. Préciser, en la justifiant, la polarité de la pile.

Compléter votre schéma en indiquant cette polarité.

3) L’équation d’oxydoréduction de fonctionnement de la pile est :

3 Cu²⁺_(aq)  +  2Al_(s)  = 3 Cu_(s)  +  2 Al³⁺_(aq)    (1)

Écrire les équations des réactions se produisant à chaque électrode.

4) La constante d’équilibre associée à l’équation (1) est K = 10²⁰⁰.

a) Déterminer le quotient initial de réaction du système ainsi constitué.

b) Le sens d’évolution du système étudié est-il cohérent ?

5) Etude de la pile en fonctionnement.

a) Déterminer les quantités de matière initiales en moles des réactifs de l’équation chimique (1). Compléter le tableau descriptif de l’évolution du système (voir annexe 3 à rendre avec la copie). En déduire la valeur de l’avancement maximal.

b) Calculer la quantité maximale d’électricité que peut débiter cette pile.

Données :    F = 9,6.10⁴ C.mol^-1 ;   M(Al) = 27,0 g.mol^–1 ;   M(Cu) = 63,5 g.mol^–1

                   Couples redox : Cu²⁺_(aq) / Cu_(s)   et     Al³⁺_(aq) / Al_(s)

 

 

ANNEXE 3  à rendre avec la copie

 

Tableau descriptif de l'évolution du système :

.

 

©Sciences Mont Blanc

 

 

 

Antilles Juin 2004 - III )Contrôle de qualité sur l'aspirine de laboratoire :

 

Des élèves souhaitent élaborer au laboratoire des comprimés d’aspirine équivalents à ceux du commerce. Ils comptent procéder en plusieurs étapes : synthèse de l’aspirine et purification, vérification de la pureté de l’aspirine, préparation des comprimés et dosage conductimétrique d’un échantillon.

I ) Synthèse de l'aspirine :

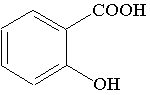
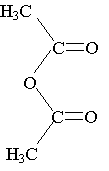
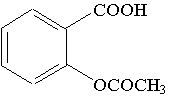
Les élèves synthétisent l’acide acétylsalicylique (ou aspirine) par réaction de m₁ = 10,00 g d’acide salicylique avec V₂ = 15,0 mL d’anhydride éthanoïque de masse volumique m₂ = 1,08 g.mL^-1.

1) Ecrire l’équation de la réaction. Donner ses caractéristiques.

 

2) La synthèse est réalisée en ajoutant quelques gouttes d’acide sulfurique au milieu réactionnel. Quel est son rôle ?

 

3) Calculer les quantités de matière initiales des réactifs (en mole).

 

4) Déterminer la masse maximale m_max d’aspirine que les élèves peuvent fabriquer.

 

5) A la fin de la synthèse, les élèves purifient l’aspirine.

Ils obtiennent une masse m_exp = 9,80 g. Calculer le rendement de la synthèse.

II ) Pureté de l'aspirine synthétisée :

Les élèves réalisent ensuite une chromatographie sur couche mince de silice avec un éluant convenable. On obtient le chromatogramme suivant :

 

 

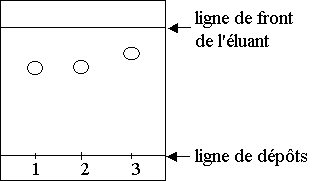
Dépôt 1 : aspirine synthétisée

 

Dépôt 2 : acide acétylsalicylique pur

 

Dépôt 3 : acide salicylique

 

 

1) Calculer le rapport frontal de l’acide acétylsalicylique.

2) L’aspirine synthétisée par les élèves est-elle pure ? (Justifier votre réponse).

III ) Dosage de l'aspirine synthétisée :

Les élèves préparent un comprimé à partir de m_i = 0,32 g d’acide acétylsalicylique synthétisé.

Ils désirent vérifier la teneur en aspirine du comprimé par dosage conductimétrique.

Pour cela, ils préparent une solution S en dissolvant le comprimé dans de l’eau distillée.

Le volume de la solution obtenue est V = 250 mL. Ils dosent V_A = 100 mL de cette solution avec une solution d’hydroxyde de sodium (Na⁺_(aq) + HO^–_(aq)) ou soude de concentration C_B = 1,0.10^–1 mol.L^–1.

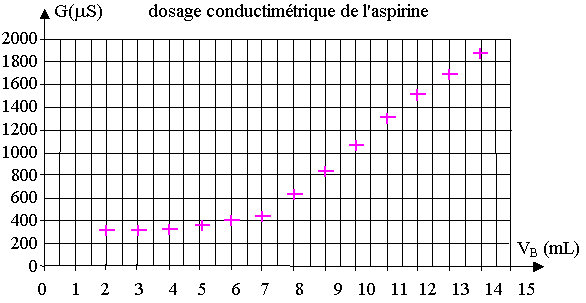
A partir des résultats obtenus par dosage conductimétrique, les élèves tracent la courbe

G = f(V_B) donnée en annexe (G étant la conductance de la solution).

1) Ecrire l’équation de la réaction acido-basique du dosage. L’acide acétylsalicylique est noté HA_(aq) et l’ion acétylsalicylate A^–_(aq).

 

2) Déterminer graphiquement le volume V_BE de soude versé à l’équivalence en expliquant votre méthode (voir annexe 4, à rendre avec la copie).

 

3) Calculer la concentration C_A en acide acétylsalicylique de la solution S (expliquer clairement votre démarche)

 

4) Déterminer la masse m_A d’aspirine contenue dans le comprimé. Ce résultat est-il attendu ?

 

Données :

Espèce chimique	Formule	Masse molaire (g.mol-1)
acide salicylique		138
anhydride éthanoïque		102
acide acétylsalicylique (aspirine)		180

 

 

Annexe 4 à rendre avec la copie

 

 

 

©Sciences Mont Blanc

 

 

Antilles Juin 2004 - III ) (spe) Dosage du glucose libre d'un jus de fruit :

1. Mélange initial :

On prélève 2,0 cm³ d’une solution de jus de fruit que l’on verse dans une fiole jaugée de 50 mL. On y ajoute 20,0 cm³ d’une solution colorée de diiode, de concentration [I_2(aq)] = 2,0.10^–2 mol.L^–1. On complète au trait de jauge par une solution d’hydroxyde de sodium afin de maintenir un excès d’ions hydroxyde dans le milieu réactionnel.

Quelle est la quantité de matière n_D de diiode initialement introduit ?

On note n_G la quantité de glucose initialement présente.

2. Réaction entre le glucose et le diiode

Le glucose G (que l’on notera RCOH) réagit avec le diiode. Il se forme des ions iodure I^–_(aq) et le glucose se transforme en ion gluconate (qui sera noté RCOO^–_(aq)). Dans le mélange étudié, on supposera que seul le diiode est coloré.

Il se produit la réaction totale :

I_2(aq) + 3 HO^–_(aq) + RCOH_(aq)  =  RCOO^–_(aq)  + 2 H₂O  + 2 I^–_(aq)

I_2(aq)  et I^–_(aq) constituent un couple oxydant réducteur ainsi que RCOH_(aq) et RCOO^–_(aq).

2.1. Ecrire la demi-équation électronique correspondant au couple I_2(aq)  et I^–_(aq).

2.2. Identifier l’espèce chimique oxydante et l'espèce chimique réductrice du couple RCOH_(aq) et RCOO^–_(aq).

2.3. Au bout d’une demi-heure l’aspect de la solution n’évolue plus, celle-ci restant partiellement colorée. Quel est le réactif limitant ?

2.4.

2.4.1. Compléter le tableau n°1, descriptif de la réaction, proposé en ANNEXE 4 qui sera

rendue avec la copie.

2.4.2. En déduire que la quantité de glucose n_G introduite dans la solution peut s’écrire :
n_G = n_D – n_R où n_R représente la quantité de diiode n’ayant pas réagi.

3. Dosage du diiode en excès

On souhaite déterminer la quantité de diiode n_R n’ayant pas réagi.

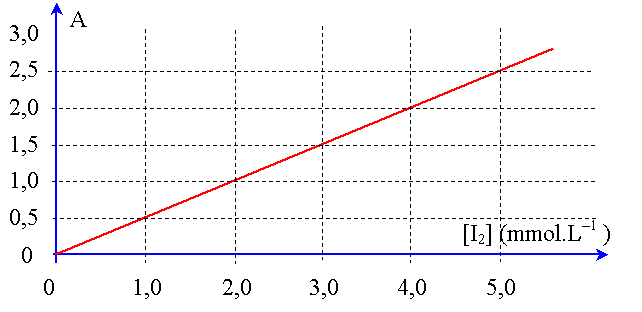
Pour cela on prépare 5 solutions de diiode de concentrations différentes et on mesure l’absorbance A de chacune à l’aide d’un spectrophotomètre.

Les valeurs obtenues permettent de tracer la courbe A = f([I₂]) proposée en ANNEXE 4 (à rendre avec la copie).

3.1. A quelle catégorie appartient une telle courbe ?

3.2. L’absorbance du mélange étudié vaut 1,5.

En utilisant la courbe A = f([I₂]) déterminer la valeur de la concentration en diiode restant dans la solution. En déduire la quantité de matière de diiode restant n_R (on rappelle que cette solution était préparée dans une fiole jaugée de 50 mL).

3.3. En utilisant la relation établie à la question 2.4.2. en déduire la quantité de glucose n_G introduite initialement ?

4. Conclusion

Calculer la quantité de glucose n’_G et la masse m_G de glucose présentes dans un litre de jus de fruits.

Donnée : masse molaire moléculaire du glucose : M_G = 180 g.mol^–1

ANNEXE 4

Tableau n°1 (x représente l’avancement de la réaction).

		I2(aq)  + 3 HO–(aq) + RCOH(aq) = RCOO–(aq) + 2 H2O + 2 I–(aq)
État initial (mol)	0	nD =	Excès	nG	0		0
État intermédiaire (mol)	x
État final en fonction de xmax (mol)	xmax	nR =

 

Courbe A = f([I₂])

 

 

 

 

 

©Sciences Mont Blanc