Sujet Bac Polynésie Juin 2004

Calculatrice autorisée

 

I ) Aïe j'ai une crampe (6,5 points)

II ) Bac à décantation à flux horizontal (5,5 points)

III ) Ondes en question (4 points)

III ) Ondes le long d'une corde (4 points)

 

I ) Aïe j'ai une crampe :

 

Lors du métabolisme basal de l'homme, l'énergie nécessaire provient de la transformation en milieu oxygéné du glucose en dioxyde de carbone et eau. Le dioxyde de carbone est transporté par le sang jusqu'aux poumons où il est alors éliminé par ventilation. Lors d'un effort physique intense, les besoins énergétiques des muscles augmentent : le métabolisme basal augmente ainsi que la ventilation. Dans certains cas, lorsque la ventilation est insuffisante, l'énergie nécessaire au fonctionnement du muscle devient insuffisante : la crampe apparaît. Il se forme, dans la cellule musculaire, de l'acide lactique qui, lorsqu'il passe dans le sang, provoque une diminution locale de son pH du fait de la création en abondance de dioxyde de carbone dissous dans le sang. Cette diminution du pH sanguin déclenche des ordres hypothalamiques qui vont amplifier la ventilation.

 

Le but de l'exercice est d'expliquer, de façon très simplifiée, les processus mis en jeu lors de l'apparition d'une crampe.

 

1) pH du sang et maintien de sa valeur :

Le sang est constitué d'un liquide plasmatique (contenant entre autres les globules et les plaquettes), qui peut être assimilé à une solution aqueuse ionique dont le pH (d'une valeur voisine de 7,4) est quasiment constant et ne peut subir que de très faibles fluctuations. Dans le cas contraire, de fortes fluctuations nuiraient gravement à la santé.

 

Le maintien de la valeur du pH se fait par deux processus :

- Le premier met en œuvre un ensemble d'espèces chimiques régulatrices dont notamment le couple acide-base CO₂ ,H₂O / HCO₃^- (couple dioxyde de carbone dissous / ion hydrogénocarbonate) grâce à l'équilibre :  CO₂ , H₂O_(aq)+ H₂O_(l) = HCO₃^-_(aq)+ H₃O⁺_(aq)  (réaction 1).

- Le deuxième processus physico-chimique est la respiration.

 

A une température de 37° C, on donne :

- pH d'un sang artériel "normal" : 7,4

- pK_A (CO₂ ,H₂O / HCO₃^-) = pKa ₁ = 6,1

 

1.1) a) Donner l'expression de la constante d'acidité Ka₁ associée au couple régulateur (réaction 1) En déduire la relation entre le pH et le pKa₁ du couple CO₂ ,H₂O / HCO₃^-.

b) Calculer alors la valeur du rapport  [HCO₃^-] / [CO₂, H₂O] dans le sang artériel normal.

c) Lors d'un effort physique. la concentration en dioxyde de carbone dissous dans le sang, au voisinage du muscle, augmente. Comment devrait varier le pH du sang ?

 

Pour éviter cette variation du pH du sang, l'hémoglobine contenue dans ce dernier et la respiration interviennent pour éliminer l'excès de dioxyde de carbone. Le transport des gaz dissous dans le sang peut être modélisé par l'équilibre :

HbO₂ + CO₂ = HbCO₂ + O₂   (réaction 2)

où Hb représente l'hémoglobine du sang.

 

1.2) Répondre qualitativement aux questions suivantes :

a) Au voisinage du poumon la quantité de O₂ dissous augmente. Dans quel sens est  déplacé l'équilibre 2 ?

b) Au voisinage du muscle la quantité de CO₂ dissous augmente. Dans quel sens est déplacé l'équilibre 2 ?

c) Expliquer comment la respiration permet de maintenir constante la valeur du pH sanguin.

 

2) L'acide lactique :

L'acide lactique a pour formule CH₃-CHOH-COOH. Sa base conjuguée est l'ion lactate

CH₃-CHOH-COO^- .

2.1) Donner la formule développée de l'acide lactique ; entourer et nommer les différents groupes fonctionnels de la molécule.

2.2) Donner la définition d'un acide selon Bronsted.

2.3) Ecrire l'équation de la réaction de l'acide lactique avec l'eau.

2.4) Dans la cellule musculaire, l'acide lactique est formé à partir de l'acide pyruvique de formule CH₃-CO-COOH. La transformation produite est une oxydoréduction faisant intervenir le couple acide pyruvique / acide lactique. 

Ecrire la demi-équation électronique associée au couple.

S'agit-il d'une oxydation ou d'une réduction de l'acide pyruvique dans la cellule musculaire ?

 

3) Variation locale du pH sanguin en l'absence des processus de maintien :

Lorsque l'acide lactique produit dans la cellule musculaire est en partie transféré dans le sang, il réagit avec les ions hydrogénocarbonate selon l'équation :
CH₃-CHOH-COOH_(aq) + HCO₃^-_(aq) = CH₃-CHOH-COO^-_(aq) + CO₂ ,H₂O_(aq)   (réaction 3)

 

Données à 37°C :

Pour le sang avant effort :    - [HCO₃^-]_i = 2,7.10^-2 mol.L^-1

                                           - [CO₂ ,H₂O]_i = 1,4.10^-3 mol.L^-1

                                           - pKa (CO₂ ,H₂O / HCO₃^- ) = pKa₁ = 6,1

                                           - pKa (acide lactique / ion lactate) = pKa₂ = 3,6

On considère un volume V = 100 ml de sang "après" effort dans lequel apparaît

n₀ = 3,0.10 ^-4 mol d'acide lactique.

3.1) Calculer la constante d'équilibre K de la réaction 3.

3.2) En supposant la transformation totale, compléter le tableau d'évolution des espèces (tableau d'avancement) fourni en annexe 1, page 9/10 ( à rendre avec la copie).

3.3) Calculer alors pour le sang après effort : [HCO₃^-]_f et [CO₂ ,H₂O]_f .

3.4) En utilisant la relation établie au 1.1.a) calculer le pH local du sang après effort.

 

Exercice I :  Annexe 1 ( à rendre avec la copie )

L'acide lactique est noté AH , sa base conjuguée A^-

Avancement	AH(aq)         +     HCO3- (aq)     =        A-(aq)        +     CO2 , H2O(aq)
Etat initial x = 0 n (mol)	n0 = 3.10 -4		0
Etat intermédiaire x
Etat final x = xmax

©Sciences Mont Blanc

 

 

 

II ) Bac à décantation à flux horizontal :

1) Etude de la chute d'une particule dans un liquide visqueux :

On prépare un mélange homogène constitué d'un liquide de masse volumique r_l = 1,0 x 10³ kg.m^-3 et de particules solides de forme sphérique de rayon R = 2,0 x 10^-6 m, de masse volumique  

r_s = 1,5 x 10³ kg.m^-3 et de masse m = 5,0 x 10^-14 kg.

 

On dépose, à la date t = 0, une fine couche (dont on néglige l'épaisseur) de ce mélange homogène à la surface d'un récipient contenant le même liquide, à l'état pur, que le mélange précédent.

 

A partir de cet instant, les particules, que l'on suppose initialement au repos, se déplacent verticalement vers le fond du récipient.

On suppose que la vitesse limite est suffisamment faible. Dans cette hypothèse, les particules sont soumises à leur poids P , à la poussée d'Archimède p = – 4/3 p.R³.r_l.g  et à une force de frottement F = - f . v  où f vaut 3,1 x 10^-12 kg.s^-1 et représente le coefficient de frottement.

On donne g = 9,8 N.kg^-1.

Pour étudier le mouvement de la particule, on se place dans un repère unidimensionnel d'axe Oz vertical et dirigé vers le bas, d'origine O au niveau de la surface libre du liquide. (voir annexe 2 page 9/10).

1.1) En effectuant une analyse dimensionnelle, vérifier que l'unité du coefficient de frottement est bien le kg.s^-1.

1.2) Compléter l'annexe 2 en faisant figurer les forces s'exerçant sur la particule pendant sa chute à l'instant 1.

1.3) En appliquant la deuxième loi de Newton, montrer que l'équation différentielle relative à la vitesse de la particule est :   dv/dt + f.v / m = g.( r_S - r_l ) / r_S .

1.4) En déduire que la valeur de la vitesse limite atteinte par les particules s'exprime par la relation

v_l = ( (r_S - r_l)/ r_l ).m.g / f .  Calculer v_l .

1.5) La solution de l'équation différentielle établie à la question 1.3 est de la forme :

                                          v(t) = v_l.( 1 – e ^{– f.t / m} )

Déterminer la date t₁ à partir de laquelle la valeur de la vitesse vaudra 99 % de la valeur de la vitesse limite.

1.6) Une étude expérimentale a permis d'obtenir le graphe, donné ci-après représentant les variations de la vitesse de la particule au cours du temps.

 

 

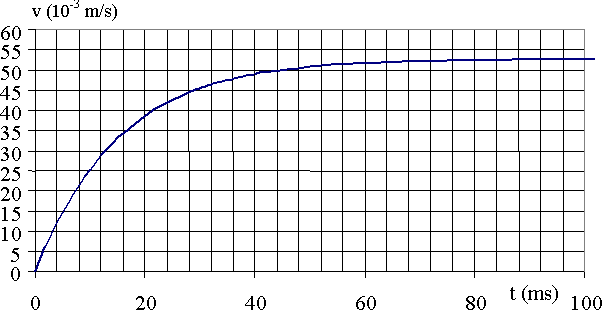
a) Déterminer par une méthode de votre choix le temps caractéristique t₁ de l'évolution de la vitesse.

b) Décrire et nommer les phases du mouvement de la particule entre les instants t = 0 et t' =100 ms

 

2) Application : modélisation simple d'un bac à décantation à flux horizontal.

Le principe d'un bac à décantation à flux horizontal consiste à faire circuler, à vitesse constante v_h un courant d'eau contenant des particules de masses différentes dans un dispositif que l'on peut modéliser de la façon suivante :

 

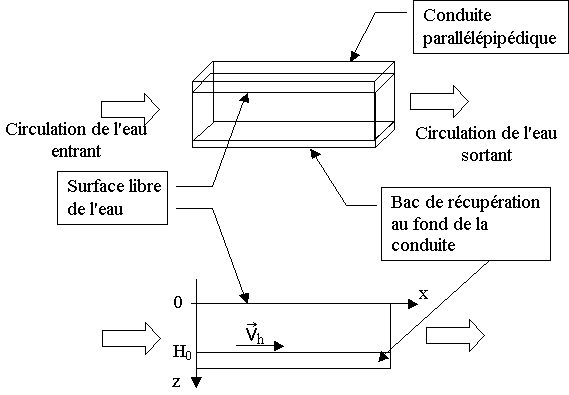
En fonction des caractéristiques des particules, ces dernières vont tomber au fond du bac en des endroits différents. On peut donc, par ce procédé, séparer les particules de nature différente contenues dans l'eau.

 

On s'intéresse au mouvement d'une particule (identique à celle de la partie 1) initialement à la surface de l'eau, à la côte z = 0 et pénétrant dans le bac en x = O.

2.1) En imaginant que la particule reste à la surface de l'eau, quel temps t₂  mettrait-elle pour parcourir la longueur du bac L = 1,0 m, si la vitesse de circulation d'eau est constante et de valeur

v_h = 0,10 m.s^-1 ?

2.2) En comparant les valeurs de t₁ (déterminé à la question 1.6.a) et t₂ , justifier que l'on puisse considérer que la vitesse de la particule dans la conduite est  v = v_h + v_l  (où V_l est la valeur de la vitesse limite atteinte en chute libre dans le fluide).

2.3) On déduit de l'étude précédente les grandeurs cinétiques données en annexe 3, page 9/10

(à rendre avec la copie). Compléter la dernière ligne du tableau.

2.4) En déduire que la trajectoire z = f(x) est une droite de coefficient directeur :

                                          a = ((r_s - r_l)/ r_s).m.g / (f.v_h)

En réalité les particules ne sont pas toutes identiques et sont caractérisées par leur masse m.

2.5) Calculer la valeur de la masse m_c de la particule pour que cette dernière tombe dans le bac à récupération au point de coordonnées x = L et z = H₀ = 0,54 m.

2.6) Dans quelle zone vont tomber les particules de masses m et de même masse volumique r_s :

si m < m_c ?    si m > m_c ?  . Justifier votre réponse.

 

 

Exercice II : Annexe 2 ( à rendre avec la copie)

 

 

 

Exercice II : Annexe 3 ( à rendre avec la copie )

 

	Projection selon Ox	Projection selon Oz
Accélération	ax(t) = 0	aZ(t) = 0
vitesse	vx(t) = vh	vz(t) = vl
Position	x(t) =	z(t) =

 

         

©Sciences Mont Blanc

 

 

 

III ) Ondes en question :

 

Les questions sont indépendantes.

 

Répondre aux questions suivantes en justifiant toutes vos réponses :

 

Question 1 :

On excite l'extrémité d'une corde à une fréquence de 50 Hz. Les vibrations se propagent le long de la corde avec une célérité de 10 m.s^-1  . Quelle est la longueur d'onde ?

 

Question 2 :

Un faisceau de lumière, parallèle monochromatique, de longueur d'onde l, arrive sur une fente horizontale de largeur a (a est de l'ordre du dixième de millimètre). Quelle figure de diffraction parmi celles proposées dans l'annexe 4, schéma 1, page 10 observe-t-on sur l'écran situé à une distance D, grande devant a.

 

Question 3 :

a) La fréquence d'une radiation lumineuse monochromatique, qui passe d'un milieu transparent à un autre milieu d'indice plus élevé, ne change pas.

b) La longueur d'onde d'une radiation monochromatique qui passe d'un milieu transparent à un autre milieu d'indice plus élevé ne change pas.

Ces affirmations sont-elles vraies ou fausses ?

 

Question 4 :

La célérité du son dans l'air est v = (k.T / M ) où T est la température absolue (en Kelvin) et  

M la masse molaire du gaz; k étant une constante.

4.1) La célérité du son diminue-t-elle quand la température augmente?

4.2) La célérité du son varie-t-elle avec la fréquence ?

4.3) La célérité du son dans l'air est-elle de l'ordre de 1 000 km.s^-1 ?

 

Question 5 :

Un pêcheur à la ligne est au bord d'un lac tranquille. Soudain un enfant vient perturber la surface de l'eau en jetant un caillou à quelques mètres du flotteur.

Le flotteur se déplace-t-il à la célérité v de l'onde ?

 

Question 6 :

Deux ébranlements se propagent en sens contraire sur une corde tendue. On a représenté (annexe 4, schéma 2, page 10) plusieurs situations possibles après leur rencontre, Choisir celle qui est physiquement possible.

   

 

Annexe 4 – Schéma 1 – Exercice III

 

 

 

  

Schéma 2 – Exercice III

 

 

 

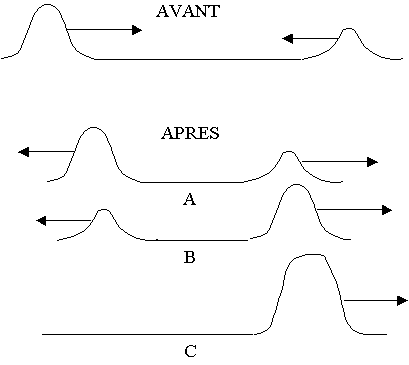©Sciences Mont Blanc

 

 

 

III ) Ondes le long d'une corde (spe):

 

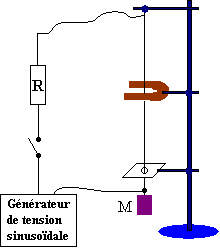
Une corde métallique, verticale, de longueur L = 1,0 m est attachée en son extrémité supérieure à un support fixe.

Son extrémité inférieure est quasiment immobilisée par une  plaque percée d’un petit trou dans lequel passe la corde.

La corde est tendue par une masse marquée M, accrochée à son extrémité inférieure; elle est parcourue par un courant électrique sinusoïdal de fréquence f = 50 Hz.

On dispose un aimant en U à cheval sur le fil, au voisinage du milieu de la corde.

Pour certaines valeurs de la masse marquée M, la corde prend un aspect particulier : on y observe un système d’un ou plusieurs fuseaux stables de même longueur.

Données :

- L’accélération de la pesanteur est g = 10 m.s^–2 ;

La célérité d’une onde se propageant sur la corde tendue est v = ( T / m )  où T est la valeur de la tension du fil (en newton) et m, sa masse linéique ou masse par unité de longueur (en kg.m^–1).

1) Comment nomme-t-on le système d’ondes qui s’établit le long de la corde ?

2) Pour une masse M = 2 kg, la corde vibre fortement en un seul fuseau.

a) Quelle est alors la longueur d’onde l des ondes progressives se propageant le long de la corde ?

b) Calculer la célérité v des ondes sur la corde.

c) En déduire la masse m de la corde.

3) La position de l’aimant et la fréquence du courant restant inchangées, on souhaite que la corde de longueur L vibre en formant plusieurs fuseaux.

a) Faut-il pour cela, augmenter ou diminuer la valeur de la masse M suspendue à la corde ? Justifier.

b) Le nombre de fuseaux produits étant impair, quel est l’état vibratoire du point situé au milieu de la corde ? Quel nom donne-t-on alors à ce point ?

4) La masse marquée suspendue à la corde est maintenant M’ = M / 4.

a) Calculer la nouvelle célérité v' des ondes sur la corde.

b) En déduire leur longueur d’onde l'.

c) Combien de fuseaux observe-t-on dans ce cas ?

d) Comment faut-il placer l’aimant pour observer les fuseaux de manière bien visible ?

©Sciences Mont Blanc