Sujet Bac Afrique Juin 2005

Calculatrice autorisée

 

I ) L'hydrogène : un combustible d'avenir ? (7 points)

II ) Voyage autour de Saturne (5 points)

III ) Utilisons le beurre pour dissoudre une tache de graisse (4 points)
III )(spe) Argentimétrie : Dosages volumétriques par précipitation (4 points)

 

 

Afrique Juin 2005 - I ) L'hydrogène : un combustible d'avenir ? :

 

Première partie : La fusion nucléaire contrôlée :

Depuis plusieurs années des recherches sont menées en Europe sur les réactions de fusion nucléaire contrôlées. Elles concernent principalement les isotopes de l’hydrogène : le deutérium et le tritium.

Le mélange réagissant doit être porté à très haute température, d’où l’expression énergie thermonucléaire désignant l’énergie libérée dans ce type de réactions.

A long terme, l’énergie thermonucléaire pourra remplacer l'énergie des centrales à fission actuelles.

 

Données

1) Eléments et noyaux :

On représente le noyau d’un atome X par le symbole  ^A_ZX.

1.1) Que représentent les deux symboles A et Z ?

1.2) Par quoi différent les isotopes d’un même élément chimique ?

1.3) Donner la composition du noyau de deutérium.

1.4) Nommer un isotope du deutérium et donner la composition de son noyau.

2) Réactions nucléaires :

Actuellement les recherches sont menées sur un mélange deutérium - tritium ; plusieurs réactions nucléaires sont possibles.

Par exemple, avec 2 noyaux de deutérium, on peut avoir la réaction (1) :

²₁H + ²₁H ® ^A1_Z1X + neutron      ou   la réaction (2) : ²₁H + ²₁H ® ^A2_Z2X + proton

Pour chacune de ces réactions (1) et (2), donner le nom et le symbole des noyaux formés : ^A1_Z1X et  ^A2_Z2X.

3) Conditions :

Pour qu’une réaction de fusion puisse se produire entre deux noyaux, il faut qu’ils soient très proches.  Il faut donc vaincre leur répulsion coulombienne.

3.1) Expliquer l’expression "la répulsion coulombienne".

3.2) Quel est le signe de la charge électrique des noyaux de deutérium et de tritium ?

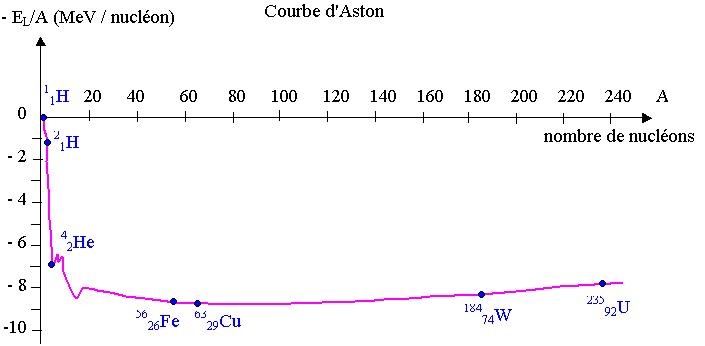
4) Courbe d’Aston :

Au cours des chocs, les noyaux sont dissociés en nucléons séparés puis de nouveaux noyaux sont formés. Il faut donc fournir de l’énergie au noyau pour le dissocier. Cette énergie comptée positivement est au moins égale à l’énergie de liaison des noyaux. Plus le noyau contient de nucléons, plus l’énergie de liaison est importante.

4.1) Rappeler la définition de l’énergie de liaison E_L.

4.2) Calculer en mégaélectronvolt (MeV) l’énergie de liaison du noyau de tritium.

4.3) Pour comparer la stabilité des noyaux entre eux, on utilise l’énergie de liaison par nucléon. La courbe d’Aston donnée en annexe représente l’opposée de l’énergie de liaison par nucléon (- E_L/A) en fonction du nombre de nucléons A. Indiquer sur la courbe, par des hachures, la zone où l’on trouve les noyaux les plus stables.

4.4) Parmi les réactions de fusion possibles dans les "tokamaks", la réaction entre le deutérium et le tritium libère le plus d’énergie.

La réaction (3) s’écrit :  ²₁H + ³₁H ® ⁴₂He + ¹₀n.

L’énergie de liaison par nucléon du noyau de tritium est d’environ 2,8 MeV.

4.4.1) Repérer sur la courbe la place du noyau de tritium.

4.4.2) Comparer à partir de la courbe d’Aston l’énergie de liaison par nucléon de ⁴₂He aux énergies de liaison de ²₁H et ³₁H . Dégager l’intérêt énergétique de la réaction (3).

5) Bilan énergétique :

Montrer que l’énergie libérée par la réaction (3) vaut 17,6 MeV.

 

 

Annexe 1 à rendre avec la copie

 

 

Deuxième partie : L'électrolyse de l'eau :

La production de dihydrogène en vue d’une utilisation énergétique semble avoir de l’avenir, que ce soit avec les piles à combustibles ou les moteurs à combustion interne.

Le dihydrogène peut être produit par électrolyse. L’objet de cet exercice est d’en étudier la production.

Dans l’industrie on utilise de l’eau pure afin d’éviter que des impuretés perturbent le fonctionnement de l’électrolyse. La cellule d’électrolyse (ou électrolyseur) est constituée de deux électrodes (cathode et anode) et d’un électrolyte ; un générateur de tension continue maintient une tension de l’ordre de 2 V permettant d’avoir une intensité du courant électrique de plusieurs kiloampères.

L’équation de la réaction qui a lieu est : 2 H₂O_(l) = 2 H_2(g) + O_2(g)

 

1) Étude de l’électrolyse :

1.1) La réaction qui a lieu dans l’électrolyseur est-elle une réaction spontanée ? Justifier votre réponse.

 

1.2) Les couples d’oxydoréduction qui participent à l’électrolyse sont O_2(g) / H₂O_(l) et H⁺_(aq) / H_2(g). Ecrire la demi-équation électronique correspondant à la formation du dihydrogène.

 

1.3) A quelle électrode se dégage le dihydrogène : cathode ou anode ? Justifier votre réponse.

 

1.4) A quel pôle du générateur cette électrode est-elle branchée ?

 

2) Intensité du courant dans l’électrolyseur :

A l’instant t₀ = 0, on démarre l’électrolyse. On cherche à connaître l’intensité I du courant qui circule dans l’électrolyseur et qui permet d’avoir une production horaire de dihydrogène de 5 m³.

À un instant t, la valeur absolue de la charge électrique Q transportée dans l’électrolyseur est donnée par la relation Q = I . Dt avec Dt = (t – t₀).

 

2.1) On considère la demi-équation électronique correspondant à la formation du dihydrogène.

On appelle x l’avancement à l’instant t de la formation du dihydrogène. Donner la relation entre la quantité de matière de dihydrogène formée n(H₂) et l’avancement x.

 

2.2) Donner la relation entre la quantité d’électrons mise en jeu n_e et l’avancement x à l’instant t.

 

2.3) Donner l’expression de la valeur absolue de la charge électrique Q à l’instant t, en fonction de l’avancement x.

 

2.4) En utilisant les relations précédentes, montrer que l’intensité I du courant qui a circulé dans l'électrolyseur pour produire la quantité de matière de dihydrogene n(H₂) est : I = 2 F . n(H₂) / Dt.

Avec F, le faraday, représentant la charge électrique transportée par une mole d’électrons.

 

2.5) On rappelle que la quantité de matière d’un gaz est proportionnelle au volume occupé par le gaz : n(H₂) = V(H₂) / V_molaire

Calculer la valeur de l’intensité I du courant qui circule dans l’électrolyseur quand le débit horaire de dihydrogène est de 5 m³.

 

Données : Dans les conditions de l’électrolyse : 25 L.mol^-1 ; F = 9,65.10⁴ C.mol^-1.

©Sciences Mont Blanc

 

 

 

Afrique Juin 2005 - II ) Voyage autour de Saturne :

En Juillet 2004, la sonde européenne Cassini-Huygens nous a livré ses premiers clichés des anneaux de Saturne.

Elle a également photographié Titan, le plus gros satellite de Saturne, situé à une distance R de Saturne. L’excentricité orbitale des satellites étant très faible, on supposera leurs trajectoires circulaires.

Dans tout l’exercice, on se place dans le référentiel saturno-centrique, centré sur Saturne et dont les trois axes sont dirigés vers trois étoiles lointaines supposées fixes.

On considère que la planète Saturne et ses satellites sont des corps dont la répartition des masses est à symétrie sphérique. Les rayons des orbites des satellites sont supposés grands devant leur taille.

Données :    G = 6,67.10^-11 S.I. :   constante de gravitation universelle.

Concernant Titan :     R_T = 1,22.10⁶ km (rayon de l’orbite de Titan).

Concernant Saturne : R_S = 6,0.10⁴ km (rayon de la planète Saturne).

                                                   T_S = 10 h 39 min (période de rotation de Saturne sur elle-même).

                                          M_S = 5,69.10²⁶ kg  (masse de Saturne).

1 ) Quelques caractéristiques de Titan :

1.1) Forces :

On considère que la seule force gravitationnelle exercée sur Titan provient de Saturne.

 

1.1.1) Nommer la (les) force(s) extérieure(s) appliquée(s) au satellite Titan, de masse M_T.

 

1.1.2) Représenter qualitativement sur un schéma, Saturne, Titan, et la(les) force(s) extérieure(s) appliquée(s) sur Titan.

 

1.1.3) Donner l’expression vectorielle de cette(ces) force(s).

 

1.2) Accélération et vitesse

On étudie le mouvement du centre d’inertie T de Titan. S est le centre d’inertie de Saturne.

Soit u  le vecteur unitaire porté par la droite ST dirigée de S vers T.

 

1.2.1) Exprimer son accélération vectorielle en précisant la loi utilisée.

 

1.2.2) On se place dans la base orthonormée (t , n ) centrée en T dans laquelle t est un vecteur unitaire porté par la tangente à la trajectoire et orienté dans le sens du mouvement et n un vecteur unitaire perpendiculaire à t et dirigé vers l’intérieur de la trajectoire

(n = - u ).

On donne l’expression de a dans la base orthonormée ( t , n): a = a_t . t + a_n . n .

Donner les expressions littérales de a_t et de a_n en fonction de la vitesse v du satellite.

 

1.2.3) A quelle composante se réduit l’accélération vectorielle a de Titan dans la base orthonormée ( t , n) ?

Compléter alors le schéma précédent, avec la base orthonormée ( t , n)  et l’accélération a de Titan.

 

1.3) Type de mouvement :

1.3.1) Montrer que le mouvement de Titan est uniforme.

 

1.3.2) Retrouver l’expression de la vitesse de Titan sur son orbite autour de Saturne :

v = (G.M_S / R_T)

 

2) D’autres satellites de Saturne :

Après le survol de Titan, la sonde Cassini a survolé le satellite Encelade en février 2005.

On peut considérer que dans le référentiel saturno-centrique, Encelade à un mouvement de révolution circulaire uniforme, dont la période (en jour terrestre), est T_E = 1,37 et le rayon est R_E.

 

2.1) Loi de Kepler :

La relation qui lie la période T de révolution d’un satellite, sa vitesse v et le rayon R de son orbite est T = 2 p R / v.   

Sa vitesse de révolution autour de Saturne est donnée par : v = (G.M_S / R)

 

2.1.1) Retrouver la troisième loi de Kepler  T² / a³ = 4 p² / (G.M_S)

 

2.1.2) Utiliser la troisième loi de Kepler pour déterminer la valeur du rayon R_E de l’orbite d’Encelade.

 

3) Sonde saturno-stationnaire :

On cherche dans cette partie à déterminer l’altitude h à laquelle devrait se trouver la sonde Cassini pour être saturno-stationnaire (immobile au-dessus d’un point de l’équateur de Saturne).

 

3.1) Quelle condition doit-on avoir sur les périodes T_S (rotation de Saturne sur elle-même) et        T_C (révolution de Cassini autour de Saturne) pour que la sonde soit "satumo-stationnaire" ?

 

3.2) Altitude de la sonde :

3.2.1) En utilisant la troisième loi de Kepler donnée à la question 2.1.1) , montrer que l’altitude h de la sonde peut se calculer avec la relation: h = ³ (T_C².G.M_S / (4 p²) – R_S

 

3.2.2) Calculer la valeur de h.

©Sciences Mont Blanc

 

 

 

Afrique Juin 2005 - III ) Utilisons le beurre pour dissoudre une tache de graisse :

A travers les quatre parties abordées, nous allons essayer de comprendre les étapes de fabrication d’un savon à partir d’un morceau de beurre, dans le but de dissoudre une tache de graisse à la surface d’un tissu.

Partie 1 : Fabrication d’un ester à partir d’un acide carboxylique

L’acide "butyrique", composé A, est un acide carboxylique de formule semi-développée

CH₃-CH₂-CH₂-COOH.  

Dans la nomenclature officielle, le nom de la molécule d’acide "butyrique" est l’acide butanoïque.

1.1) Nommer le groupe caractéristique de cette molécule et l’encadrer sur la formule semi-développée.

 

1.2) L’action de l’acide butyrique A sur un réactif B conduit à la formation de deux produits C et D.      

C a pour formule CH₃-CH₂-CH₂-COO-CH₂-CH₂-CH₃.

 

1.2.1) Nommer le produit C. A quelle famille appartient-il ?

 

1.2.2) Ecrire la formule semi-développée du réactif B et donner son nom.

1.2.3) Quelle est la nature du produit D?

Partie 2 : Synthèse d’un corps gras : la butyrine

La butyrine, appelée aussi tributyrate de glycéryle, est un corps gras (ou triester) présent dans le beurre. Cette molécule résulte de l’action de l’acide "butyrique" sur le glycérol.

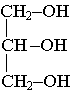
Formule semi-développée du glycérol :

 

 

 

 

2.1) En utilisant les formules semi-développées, écrire l’équation de synthèse de la butyrine.

 

2.2) On réalise et on chauffe le mélange suivant:

- une masse m₁ = 39,6 g d’acide "butyrique"

- une quantité de matière n₂ = 0,150 mol de glycérol

- quelques pierres ponces

Données : M (glycérol) = 92,0 g.mol^-1    ;   M (acide butyrique) = 88,0 g.mol^-1

Le mélange est-il stœchiométrique ?

 

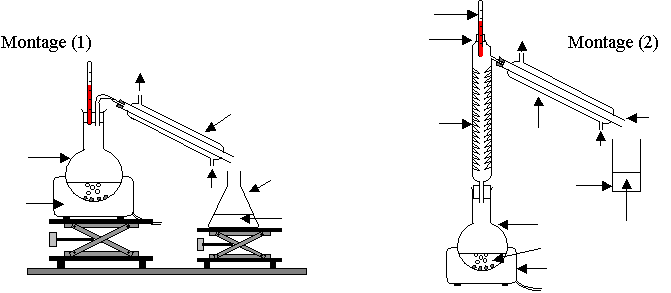
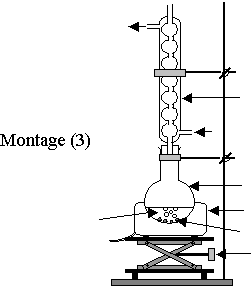
2.3) Parmi les montages (1), (2) et (3) proposés en annexe 2, lequel utiliseriez-vous pour réaliser cette synthèse ?

 

2.4) Légender le schéma du montage choisi.

 

2.5) On obtient une masse m = 29,0 g de butyrine. Calculer le rendement r de la réaction.

 

Donnée :  M (butyrine) = 302 g.mol^-1

Partie 3 : Fabrication d’un savon mou à partir de beurre :

Le beurre contient plusieurs corps gras, l’oléine, la palmitine et la butyrine.

La butyrine représente 35% en masse du beurre.

Nous n’étudierons que la réaction de fabrication du savon grâce à la butyrine.

Pour cela, nous allons faire réagir :

20 g de beurre avec un excès de potasse (K⁺_(aq) + HO^-_(aq) ) concentrée.

Après 30 minutes de chauffage, on observe, après relargage, la formation d’un précipité jaune.

 

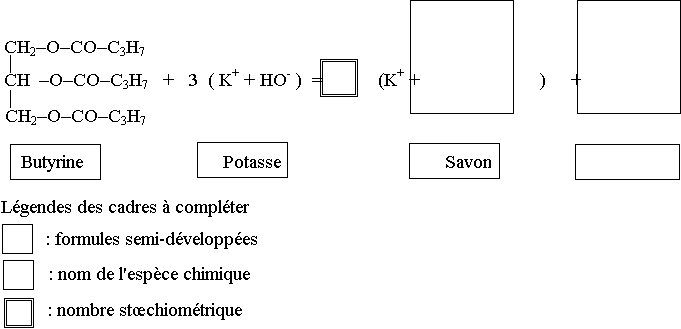
3.1) Nommer la réaction qui conduit à la formation du précipité observé et compléter son écriture, en annexe 3, en remplissant les cadres.

 

3.2) Donner deux caractéristiques de cette transformation à chaud.

 

3.3) En fait, le rendement après filtration n’est que de 85 %.

Calculer la masse de savon ainsi produite à partir de la butyrine.

 

Donnée  :  M (savon fabriqué à partir de la butyrine) = 126 g.mol^-1

Partie 4 Utilisation du savon fabriqué pour dissoudre une tache de graisse :

Après élimination de l’excès de potasse, on souhaite étudier les qualités détergentes du savon sur une tache de graisse.

 

Le savon est composé d’ions carboxylates qui peuvent être modélisés des deux façons suivantes

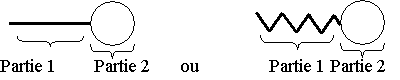
Le schéma ci-dessous représente une tache de graisse à la surface d’un tissu plongé dans l’eau savonneuse (étape N°1) et sa dislocation par action du savon synthétisé précédemment (étape N°2).

 

 

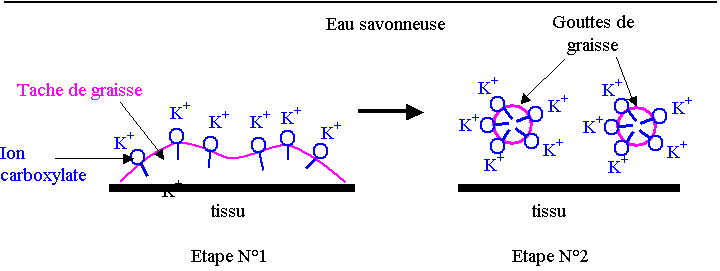
Les ions carboxylates modélisés ont été représentés, correctement orientés par rapport à l’eau et à la graisse, sur chacune des étapes N°1 et N°2.

 

4) En vous aidant du schéma précédent, identifier la composition et la propriété de chacune des deux parties de l’ion carboxylate modélisé.

 

Annexe 2   à rendre avec la copie

 

 

Annexe 3   à rendre avec la copie

Ecriture de la réaction de synthèse du savon :

 

©Sciences Mont Blanc

 

 

 

Afrique Juin 2005 - III )(spe) Argentimétrie : Dosages volumétriques par précipitation :

L’argentimétrie groupe un certain nombre de dosages faisant intervenir le nitrate d’argent AgNO₃ (totalement dissocié en Ag⁺ et NO₃^- ).

On utilise deux méthodes de dosage argentimétriques, pour lesquelles aucune connaissance spécifique préalable n’est nécessaire.

On utilise dans un premier temps la méthode Mohr afin d’étalonner la solution de nitrate d’argent à l’aide d’une solution de chlorure de sodium de concentration connue.

Puis on utilise la méthode de Charpentier-Volhard pour doser une solution d’acide chlorhydrique.

I ) Méthode de Mohr :

1) Principe

On précipite à l’état de chlorure d’argent les ions chlorure d’une solution de chlorure de sodium par addition d’une solution de nitrate d’argent à étalonner.

a) Ecrire l’équation de la réaction de dosage.

On doit posséder un indicateur de fin de réaction : les ions chromate CrO₄^2- qui donnent avec les ions argent Ag⁺ un précipité rouge brique de chromate d’argent.

b) Donner l’équation de cette réaction de précipitation

 

2) Domaine de travail

En milieu basique pH > 7,5 , il y a précipitation des ions argent en hydroxyde d’argent AgOH_(s).

En milieu acide pH < 6,5 , le chromate d’argent est soluble.

Préciser le domaine d’utilisation de la méthode de Mohr. Justifier votre réponse.

 

3) Type de dosage

Indiquer à quel type de dosage, direct ou indirect, correspond la méthode de Mohr.

 

4) Mise en oeuvre expérimentale

Dans un erlenmeyer de 100 mL à col large:

Placer une prise d’essai de V₁ = 20,0 mL de la solution connue de chlorure de sodium de concentration c₁ = 4,0.102 mol.L^-1

Ajouter 5 gouttes de solution de chromate de potassium.

Faire couler la solution de nitrate d’argent contenue dans la burette jusqu’à l’obtention d’une coloration orange de la solution.

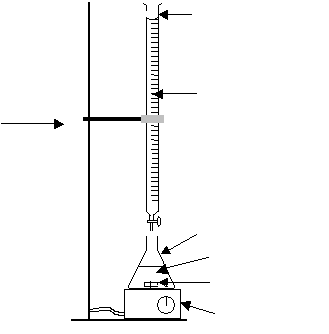
a) Compléter le schéma légendé du dispositif expérimental en Annexe 2.

Le virage est obtenu pour un volume de solution de nitrate d’argent versé: V_eqi = 18,2 mL.

b) En déduire la concentration de la solution de nitrate d’argent.

II ) Méthode de Charpentier-Volhard :

1) Principe

A une prise d’essai de la solution d’acide chlorhydrique à titrer, contenant n₀(Cl^-) moles d’ions chlorure, on ajoute un excès connu n₀(Ag⁺) de moles d’ions argent issus d’une solution de nitrate d’argent de concentration c₀ = 5,0.10^-2 mol.L^-1

a) Ecrire l’équation de cette première réaction consommant des ions argent.

L’excès d’ions argent est précipité sous forme AgSCN_(s) par des ions thiocyanate SCN^-_(aq) .

Soit n_eq(SCN^-) la quantité de matière ajouté à l’équivalence.

b) Ecrire l’équation de cette deuxième réaction consommant des ions argent.

c) Retrouver la relation à l’équivalence :         n₀(Ag⁺) = n₀(Cl^-) + n_eq(SCN^-)

On utilise comme indicateur de fin de réaction, l’ion fer III qui donne avec les ions thiocyanate un ion complexe rouge sang.

 

2) Domaine de travail

En milieu basique pH > 7,5 , AgOH_(s) précipite.

Par ailleurs, l’hydroxyde de fer(III) : Fe(OH)₃ précipite à pH >2.

a) Préciser le domaine d’utilisation de la méthode de Charpentier-Voihard. Justifier votre réponse.

b) Aurait-on pu utiliser la méthode de Mohr pour doser les ions chlorure de cette solution d’acide chlorhydrique ? Justifier votre réponse.

 

3) Type de dosage

A quel type de dosage, direct ou indirect, correspond la méthode de Charpentier-Volhard ?

 

4) Mise en oeuvre expérimentale

Dans un erlenmeyer de 100 mL à col large:

Placer une prise d’essai de V_A = 10,0 mL de la solution d’acide chlorhydrique: celle-ci contient les ions chlorure à doser à la concentration c_A.

Ajouter environ 5 mL de solution d’acide nitrique.

Ajouter V₀ = 25,0 mL de la solution de nitrate d’argent de concentration c₀ = 5,0.10^-1 mol.L^-1 .

Ajouter environ 5 mL de solution contenant des ions Fe³⁺_(aq).

Faire couler la solution de thiocyanate contenue dans la burette

(de concentration c₂ = 4,0.10^-2 mol.L^-1) jusqu’à l’obtention d’une coloration rouge.

Le virage est obtenu pour un volume de solution de thiocyanate d’ammonium versé V_eq2 = 8,0 mL.

Déduire de la relation donnée au II ) 1) c), la concentration c_Ade la solution d’ions chlorure.

 

 

Annexe 2      à rendre avec la copie

 

 

©Sciences Mont Blanc