Sujet Bac Asie Juin 2005

Calculatrice NON autorisée

Une très longue corde élastique inextensible est disposée horizontalement sur le sol. Un opérateur crée une perturbation en imprimant une brève secousse verticale à l'extrémité S de la corde.

1 ) Considérations générales :

1.1) Préciser la direction de propagation et la direction du mouvement du point M.

1.2) En déduire si l'onde est transversale ou longitudinale.

2 ) Etude chronophotographique :

La propagation de l'onde le long de la corde est étudiée par chronophotographie (figure 2).

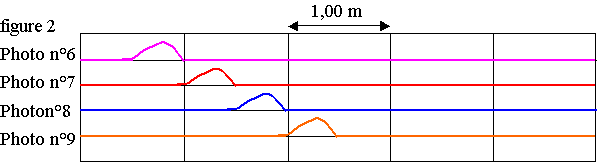
L'intervalle de temps séparant deux photos consécutives est Dt = 0,25 s.

2.1) Définir puis calculer la célérité de l'onde.

2.2) Pendant quelle durée un point de la corde est-il en mouvement ?

3 ) Evolution temporelle du déplacement vertical de plusieurs points de la corde :

L'évolution au cours du temps des altitudes z_A et z_B de deux points A et B de la corde est l'objet de la figure 3.

L'instant de date t₀= 0 s correspond au début du mouvement de S.

Toutes les réponses doivent être justifiées.

3.1) Lequel de ces deux points est touché le premier par la perturbation ?

3.2) Lequel de ces deux points est situé le plus près du point source S ?

3.3) Quel retard le point touché en second présente-il dans son mouvement par rapport au point touché en premier ?

3.4) Quelle est la valeur de la distance séparant les deux points A et B ?

3.5) Un troisième point C commence son mouvement à l'instant de date t_C= 0,50 s.

Préciser sa position par rapport à A.

Représenter sur un schéma la position des points A, B et C ( échelle 2 cm pour 1 m) par rapport au point source S.

4 ) Influence de quelques paramètres sur la célérité de l'onde :

Les courbes ci-dessous ( figures 4, 5 et 6) donnent l'évolution au cours du temps du déplacement vertical d'un point K d'une corde situé à la distance fixe d = SK du point source S ; l'instant de date t₀ = 0 s correspond au début du mouvement de S ; les conditions expérimentales sont précisées pour chaque expérience.

Toutes les réponses doivent être justifiées en utilisant les représentations graphiques.

On étudie successivement l'influence de :

- la forme de la perturbation;

- la tension de la corde;

- la nature de la corde.

4.1) Influence de la forme de la perturbation .

La même corde est utilisée ; sa tension est la même dans toutes les expériences.

La forme de la perturbation modifie-t-elle la célérité ?

4.2) Influence de la tension de la corde.

La même corde est utilisée ; lors de l'expérience 2-a, sa tension est plus faible que lors de l'expérience 2-b.

La tension de la corde modifie-t-elle la célérité et si oui, dans quel sens ?

4.3) Influence de la nature de la corde.

Rappel : la masse linéique m est la masse par unité de longueur ; pour une corde de masse M et de longueur L on a donc :

m = M / L.

La tension est la même dans les deux expériences ; la masse linéique de la corde utilisée pour l'expérience 3-a est plus faible que celle de la corde utilisée pour l'expérience 3-b.

La masse linéique de la corde modifie-t-elle la célérité et si oui, dans quel sens ?

©Sciences Mont Blanc

Asie Juin 2005 - II ) Evolution temporelle de différents systèmes électriques :

Toutes les questions de cet exercice sont indépendantes.

1 ) Etude comparative des dipôles RL, RC, RLC série.

On réalise successivement les circuits correspondant aux montages 1, 2 et 3.

Dans le montage 1, le condensateur est initialement déchargé, alors que dans le montage 3, il est initialement chargé. Le sens positif de l'intensité du courant i est indiqué sur les schémas.

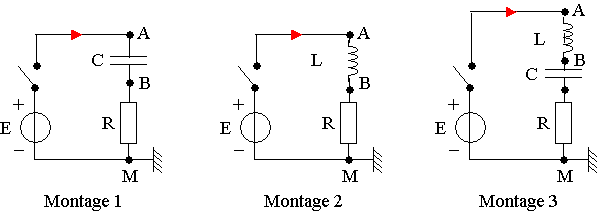
1.1) On visualise à l'aide d'un système approprié la tension u_R aux bornes du conducteur ohmique.

1.1.1) Préciser entre quels points on doit réaliser le branchement.

1.1.2) Expliquer pourquoi on visualise alors les variations de l'intensité du courant.

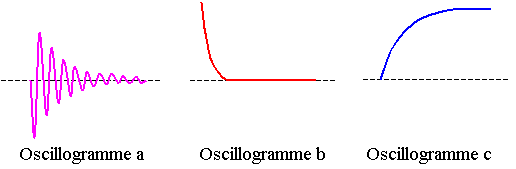
1.2) On ferme l'interrupteur et on observe, à partir des montages précédents, les oscillogrammes a, b et c. Le trait pointillé correspond à la trace du spot en l'absence de tension sur les deux voies. Affecter à chaque montage l'oscillogramme correspondant. Justifier brièvement les réponses.

2 ) Exemple d'application : flash d'appareil photo jetable.

Certains appareils photographiques sont équipés d'un flash dont le principe de fonctionnement est expliqué ci-dessous :

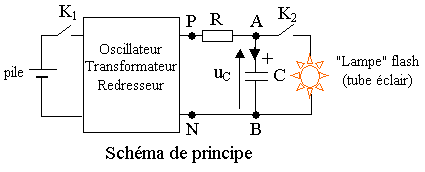1^ère phase :

A la fermeture de l'interrupteur K₁, la pile alimente l'oscillateur qui délivre alors une tension alternative; celle-ci peut être élevée grâce au transformateur ; le redresseur permet d'obtenir une tension continue de l'ordre de quelques centaines de volts entre les points P et N. Le condensateur se charge et emmagasine de l'énergie.

2^ème phase :

Au moment où le photographe appuie sur le déclencheur, l'interrupteur K₂ se ferme et le condensateur libère alors quasi instantanément l'énergie emmagasinée dans la lampe, ce qui produit un flash lumineux

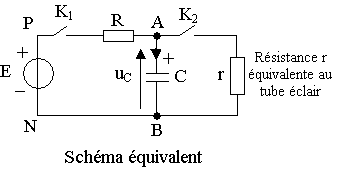Le schéma équivalent au schéma de principe de la page précédente est représenté ci-contre :

Données :

C = 100 mF ;

u_C : tension aux bornes du condensateur ;

+ : sens positif du courant dans la branche AB.

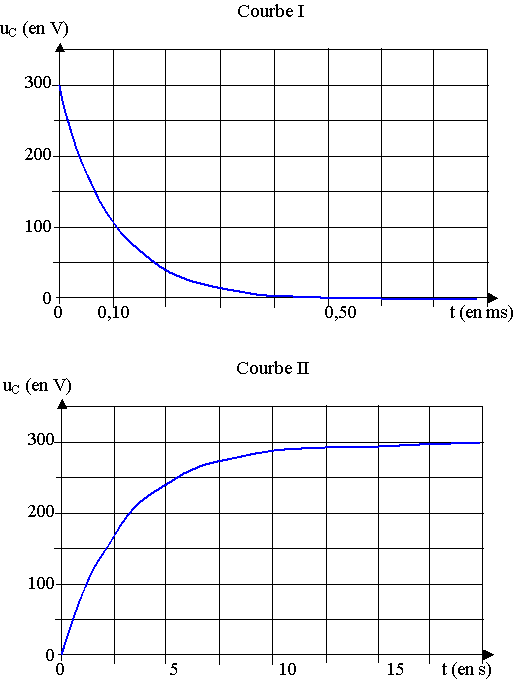
Une étude expérimentale du dispositif a permis d'obtenir les courbes I et II de l'annexe (à rendre avec la copie) .

2.1) Identification des courbes :

2.1.1) Associer à chaque phase de fonctionnement du flash décrite précédemment, les phénomènes de charge et de décharge du condensateur.

2.1.2) Affecter à chacune des courbes (I et II) la phase correspondante.

2.2) Evolution temporelle du système lors des deux phases :

Les courbes I et II de l'annexe permettent d'évaluer la constante de temps t lors de chacune des phases.

Expliquer et utiliser une méthode au choix permettant de déterminer t.

Vérifier sur l'annexe qu'on obtient t(courbe I) » 0,1 ms et t(courbe II) » 3 s.

En déduire les valeurs approchées de R et r.

2.3) Puissances mises en jeu lors des deux phases :

La puissance moyenne P, mise en jeu lors d'un échange d'énergie DE pendant la durée D t, est donnée par la relation :

P = ½DE½ / D t avec DE en joules, Dt en secondes et P en watts.

2.3.1) Quelle est la tension maximale aux bornes du condensateur ?

2.3.2) En déduire l'énergie maximale emmagasinée par le condensateur.

2.3.3) On considère que la charge et la décharge est complète à t = 5 t.

Utiliser les valeurs indiquées au paragraphe 2.2.2) pour calculer la puissance moyenne mise en jeu lors de chaque phase. Quel est l'intérêt pratique de la différence constatée ?

En déduire pourquoi la résistance r du tube éclair doit être si petite.

2.4) Etude théorique du dispositif utilisé :

2.4.1) Préciser le signe des charges portées par chacune des armatures du condensateur lorsqu'il est chargé. Indiquer, lors de chaque phase, si le courant circule dans la branche AB dans le sens positif choisi en justifiant brièvement.

2.4.2) Etablir l'équation différentielle vérifiée par u_C c'est à dire la relation entre la fonction u_C(t) et sa dérivée par rapport au temps lors de chacune des phases de fonctionnement.

Annexe ( à rendre avec la copie)

©Sciences Mont Blanc

Asie Juin 2005 - III ) Hémisynthèse de l'aspirine, contrôle de la pureté du produit formé :

Données :

	acide salicylique	acide acétylsalicylique (aspirine)	anhydride éthanoïque ou acétique
Formule
Masse molaire moléculaire (g.mol^-1)	138	180	102
Masse volumique (g.mL^-1)			1,08
Solubilité dans l'eau	peu soluble	peu soluble
Solubilité dans l'éthanol	très soluble	soluble

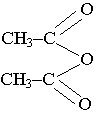
Réactivité de l'anhydride acétique avec l'eau : l'anhydride acétique réagit totalement et vivement avec l'eau en donnant de l'acide acétique.

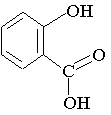
1 ) La molécule d'aspirine :

Recopier la formule de la molécule d'aspirine ou acide acétylsalicylique ; entourer et nommer les groupes fonctionnels (ou caractéristiques) oxygénés présents dans cette molécule.

2) Etude de la préparation :

Lors d'une séance de travaux pratiques, on envisage de préparer l'aspirine. Différents réactifs sont proposés aux élèves : acide acétique (ou éthanoïque), anhydride éthanoïque, acide salicylique.

Un débat s'engage sur le choix à effectuer.

Un groupe propose de faire réagir l'acide salicylique avec l'acide acétique.

2.1) Ecrire l'équation de la réaction modélisant la transformation proposée, en utilisant les formules semi-développées.

2.2) L'avancement maximal peut-il être atteint ? Pourquoi ?

2.3) Donner un moyen d'augmenter l'avancement final en conservant les mêmes réactifs.

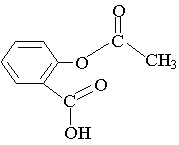
Après discussion, les élèves décident d'utiliser l'anhydride éthanoïque à la place de l'acide acétique.

2.4) Ecrire l'équation de la réaction modélisant cette transformation, en utilisant les formules semi-développées.

Ils se réfèrent au protocole suivant :

Hémisynthèse de l'aspirine réalisée sous la hotte

· Dans un ballon bien sec de 250 mL, introduire 13,8 g d'acide salicylique, environ 25 mL d'anhydride éthanoïque ( alors en excès).

· Ajouter 10 gouttes d'acide sulfurique concentré.

· Adapter au ballon un réfrigérant à boules et chauffer à reflux au bain marie pendant 15 minutes en agitant par intermittence.

Cristallisation du produit obtenu :

· Arrêter le chauffage, sortir le ballon du bain-marie et verser, sans attendre le refroidissement de façon progressive environ 30 mL d'eau distillée par le haut du réfrigérant. Prendre garde aux vapeurs chaudes et acides.

· Quand l'ébullition est calmée, ôter le réfrigérant après avoir arrêté la circulation d'eau et agiter jusqu'à l'apparition des premiers cristaux.

· Ajouter 50 mL d'eau glacée et placer le ballon dans un bain d'eau glacée pendant 5 min.

· Filtrer sur büchner le contenu du ballon en tirant sous vide avec la trompe à eau ; rincer le ballon à l'eau distillée froide, verser dans le filtre.

· Laver les cristaux à l'eau distillée froide, essorer et les récupérer dans un erlenmeyer.

2.5) Pourquoi utiliser un ballon bien sec ?

2.6) Quel est le rôle de l'acide sulfurique ?

2.7) Pourquoi chauffer ?

2.8) Quel est l'intérêt d'un chauffage à reflux ?

2.9)Quel est le rôle des 30 mL d'eau distillée, ajoutés par le haut du réfrigérant, après le chauffage?

2.10) Faire un schéma annoté de la filtration sous vide.

3 ) Etude qualitative de la réaction :

Un groupe d'élèves a pesé 12,0 g de cristaux après séchage.

Définir puis calculer le rendement de la synthèse effectuée par ce groupe d'élèves.

4 ) Contrôle de la pureté :

On introduit la totalité des cristaux dans une fiole de 100,0 mL. On ajoute un peu d'éthanol afin de dissoudre l'aspirine et on complète au trait de jauge avec de l'eau distillée. On prélève V_A= 10,0 mL de cette solution que l'on titre avec une solution d'hydroxyde de sodium de concentration molaire apportée c_B= 5,0 10^-1 mol.L^-1.

A l'équivalence, le volume de solution d'hydroxyde de sodium versé est V_BE= 10,0 mL.

4.1) En notant HA l'aspirine, écrire l'équation de la réaction de titrage.

4.2) En déduire la quantité de matière d'aspirine pure présente dans l'échantillon titré, puis celle présente dans les cristaux.

4.3) L'aspirine préparée est-elle pure ?

Asie Juin 2005 - III )(spe) Etude de différents sons :

D’après Encyclopédie Microsoft® Encarta® 2002.

Violon : instrument de musique à cordes frottées à l’aide d’un archet ; le plus célèbre des instruments de l’orchestre.

Les cordes du violon, mises en mouvement par l’archet, transmettent leurs vibrations au chevalet, qui les répercute sur la table d’harmonie ; celle-ci les amplifie et les transmet, par l’âme au fond.

Cet exercice ne nécessite aucune connaissance musicale.

1 ) Les fonctions d’un instrument de musique :

Quelles sont les deux fonctions que doit remplir un instrument de musique pour produire un son ? A partir du texte précédent, indiquer le nom des parties du violon qui remplissent ces fonctions.

2 ) Etude des sons produits par différents instruments :

Un microphone est relié à un ordinateur. Différents instruments sont placés devant ce microphone. On réalise une acquisition des sons émis par ces instruments, puis, pour certains, une analyse spectrale à l’aide d’un logiciel adapté.

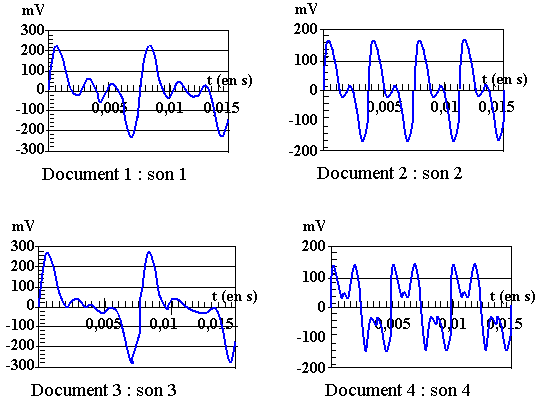
Un son est caractérisé par des propriétés physiologiques : intensité, hauteur, timbre. L’étude des courbes obtenues lors des acquisitions (documents 1 à 4) permet de retrouver certaines de ces propriétés.

2.1) Deux des sons étudiés correspondent à la même note.

2.1.1) Quelle est alors leur propriété physiologique commune ?

Nommer la grandeur physique associée.

2.1.2) Identifier les documents correspondants et mesurer cette grandeur.

2.1.3) Sont-ils obtenus avec le même instrument ? Pourquoi ?

Quelle est la propriété physiologique mise en jeu ?

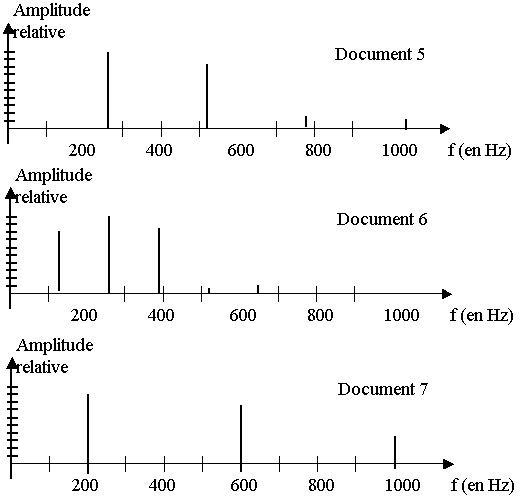
2.2)Les documents 5 et 6 correspondent à l’analyse spectrale des sons relatifs aux documents 1 et 2.

2.2.1) Pour chacun des deux sons, déterminer la fréquence fondamentale. Donner les fréquences des harmoniques. Quel est le rapport entre les fréquences des harmoniques et celle du fondamental ?

2.2.2) Attribuer chaque spectre de fréquence au son correspondant.

2.3) Le son n°4 a été produit en pinçant une corde tendue entre deux points fixes selon le dispositif suivant :

On pince la corde. Elle vibre suivant ses différents modes propres de vibration.

2.3.1) En utilisant le spectre de ce son (document 7), déterminer sa fréquence fondamentale f.

Le mode propre de vibration de fréquence f correspond à une onde stationnaire produite par la propagation entre A et B d’une onde progressive sinusoïdale de longueur d’onde l.

On rappelle l’expression de la célérité v d’une onde sur une corde tendue :

v = ( F / m )

F (en N) étant la tension et m (en kg.m^-1) la masse linéique ou masse par unité de longueur de la corde.

2.3.2) Exprimer L en fonction de l pour que cette onde stationnaire correspondant à la fréquence fondamentale puisse s’établir.

2.3.3) Rappeler la relation entre la célérité v, la fréquence f d’une onde sinusoïdale et la longueur d’onde l.

2.3.4) La corde utilisée a une masse linéique égale à 7,5.10^–4 kg.m^-1. Exprimer puis calculer la valeur de la tension de la corde AB pour qu’elle émette le son étudié.

2.3.5) Si on diminue cette tension, le son émis devient-il plus grave ou plus aigu ? Justifier.