Sujet Bac Nouvelle Calédonie Mars 2005
Calculatrice autorisée
I ) La tomographie par émission de positons : Une technique d'imagerie médicale (4 points)
II ) Le dihydrogène pour la protection de l'environnement(6,5 points)
III ) Oscillateur solide-ressort (5,5 points)
I )(spe) La lunette de Kepler (4 points)
Nouvelle Calédonie Mars 2005 - I ) La tomographie par émission de positons : Une technique d'imagerie médicale :
« Les neurobiologistes disposent d’une panoplie de techniques d’imagerie dont chacune révèle des aspects particuliers de l’architecture et du fonctionnement du cerveau. […] La tomographie par émissions de positions, TEP, […] donne accès aux variations du flux sanguin, lesquelles reflètent l’activité métabolique cérébrale, […].
De cette découverte a germé l’idée que l’on […] pourrait observer de l’extérieur l’activité siégeant à l’intérieur du crâne.
En TEP, on détecte les molécules d’eau [présentes en grande quantité dans le cerveau] en utilisant de l’eau radioactive que l’on injecte au sujet par voie intraveineuse. […]. Dans ces molécules d’eau radioactives, le noyau d’oxygène qui contient normalement huit protons et huit neutrons est remplacé par un noyau d’oxygène qui ne comporte que huit protons et sept neutrons : c’est l’oxygène 15. L’oxygène 15 est un émetteur b+ : un de ses protons se transforme rapidement en neutron, en émettant un positon(1) et un neutrino(2). »
D’après un article de la revue Pour la Science, N° 302, décembre 2002.
(1) Le positon est aussi appelé positron.
(2) Le neutrino est une particule de symbole 00n .
Données numériques :
|
Noyaux et particules |
126C |
157N |
158O |
155F |
Electron |
Positon |
Neutron |
Proton |
|
Energie de liaison par nucléon El/A (MeV.nucléon-1) |
6,676 |
7,699 |
7,463 |
6,483 |
- |
- |
- |
- |
|
Masse (kg) |
- |
- |
- |
- |
9,109.10–31 |
9,109.10–31 |
1,67492.10–27 |
1,67262.10–27 |
Célérité de la lumière dans le vide : c = 2,998.10 8 m.s-1
1 eV = 1,602.10 -19 J
1 ) La désintégration de l’oxygène 15 :
1.1) Donner, en la justifiant, l’écriture symbolique AZX du noyau d’oxygène 15.
1.2) Ecrire l’équation de la réaction de désintégration du noyau d’oxygène
15, sans énoncer les lois de conservation et sans tenir compte de l’émission
du neutrino mentionné dans le texte.
Le noyau fils n’est pas produit dans un état excité.
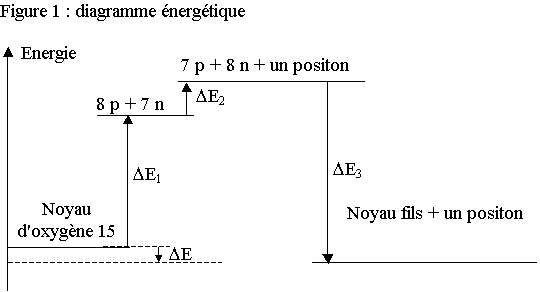
1.3) La variation d’énergie DE du système lors de la désintégration
d’un noyau d’oxygène 15 est indiquée sur la figure 1. Elle peut être calculée
en utilisant le digramme énergétique de cette figure.
1.3.1) Définir l’énergie de liaison El du noyau.
1.3.2) On rappelle que l’énergie de liaison par nucléon est notée El / A .
Calculer, en MeV, la variation d’énergie DE1 indiquée sur la figure 1.
Par un calcul identique, on trouve DE1 = 111,9 MeV.
1.3.3) En utilisant les masses des particules, calculer, en MeV, la variation d’énergie DE2 indiquée sur la figure 1 (on donnera le résultat final avec deux chiffres significatifs).
1.3.4) Déduire des résultats précédents la valeur, exprimée en MeV, de la variation d’énergie DE du système lors de la désintégration d’un noyau d’oxygène 15.
2 ) L’utilisation de l’oxygène 15 en TEP
« Le positon est l’antiparticule de l’électron, […]. Matière et antimatière s’annihilent(3) dès qu’elles sont en présence : un positon et un électron du milieu environnant s’annihilent en libérant une paire de photons d’énergie déterminée (511 kiloélectronvolts). Les deux photons sont émis dans deux directions diamétralement opposées. […]
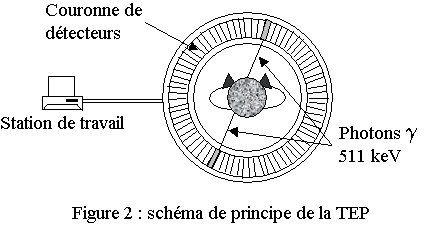
L’objet de la TEP est de repérer les photons […], très énergétiques, [qui] traversent en grande partie le cerveau et le crâne, de sorte que l’on peut les détecter en dehors de la boite crânienne. Le dispositif de détection, la caméra à positons, […] entoure la tête du sujet. […] Lorsqu’une paire de photons gamma de 511 kiloélectronvolts arrive simultanément sur deux détecteurs […], on admet qu’ils sont issus de la dématérialisation d’un même positon (figure 2). […]. Après l’analyse mathématique, on obtient une série de « coupes » contiguës du cerveau qui représentent la concentration en noyaux d’oxygène 15 en chaque point ce qui reflète le débit sanguin local.
Enfin, le temps de demi-vie de ces noyaux d’oxygène 15 émetteurs de positons est bref : 123 secondes. Cette propriété est importante dans le contexte de l’utilisation de ces molécules chez l’homme, car, d’une part l’irradiation subie par les sujets est faible et d’autre part cette radioactivité disparaissant rapidement, on peut faire plusieurs études chez le même sujet.
Cette courte durée de vie impose néanmoins que l’eau radioactive soit préparée dans les minutes qui précèdent son injection, et que deux injections successives soient espacées de 8 à 10 minutes. »
(3) Annihiler : réduire à rien ; détruire,
anéantir. En physique, transformation intégrale de l’énergie de masse en énergie
transportée par une onde électromagnétique.
2.1) Définir le temps de demi-vie t1/2 .
2.2) L’évolution temporelle du nombre de noyaux d’oxygène 15 est donnée par
la loi de décroissance où N0 est le nombre de noyaux d’oxygène
15 au moment de l’injection à l’instant de date t = 0 s.
2.2.1) A partir de cette loi, montrer que la constante radioactive l a pour expression : l = ln 2 / t1/2.
2.2.2) Calculer sa valeur.
2.3) Si l’on souhaite poursuivre l’examen par TEP, on estime qu’il est nécessaire
de procéder à une nouvelle injection dans l’organisme du patient lorsque le
nombre N(t1) de noyaux d’oxygène 15 restant à l’instant de date
t1 est de l’ordre de 5% du nombre N0 de noyaux initialement
injectés.
Calculer la valeur de la date t1.
2.4) Justifier la durée d’espacement des injections évoquée dans le texte.
3 ) La détection du rayonnement gamma :
3.1) En utilisant le texte, écrire l’équation de la réaction ayant lieu lors de la rencontre d’un positon, issu de la désintégration d’un noyau d’oxygène 15, avec un électron du milieu environnant. On notera g chaque photon gamma émis.
3.2) On admet que l’énergie libérée par cette réaction est partagée également
entre les deux photons dont la masse est nulle. Calculer l’énergie de chaque
photon gamma émis. Est-elle en accord avec celle donnée dans le texte (aucun
calcul d’écart relatif n’est demandé) ?
©Sciences Mont Blanc
Nouvelle Calédonie Mars 2005 - II ) Le
dihydrogène pour la protection de l'environnement:
Les parties 1 et 2 sont indépendantes
Le principe de la pile à combustible, une technique déjà ancienne, consiste à utiliser du dihydrogène pour stocker et transporter l’énergie. En effet le dihydrogène semble être le carburant par excellence pour les véhicules du futur, face aux préoccupations environnementales croissantes.
Une pile à combustible est un assemblage de cellules élémentaires, en nombre suffisant pour assurer la production électrochimique d’électricité dans les conditions de tension et d’intensité voulues.
1 ) Principe de fonctionnement d’une cellule élémentaire :
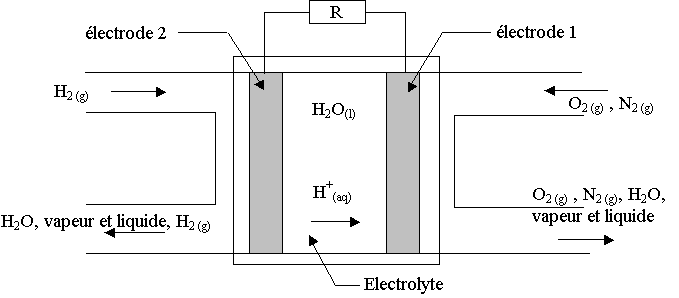
De façon générale, le fonctionnement électrochimique d’une cellule élémentaire de pile à combustible peut être schématisé selon le schéma de l'annexe à rendre avec la copie.
Chaque cellule élémentaire est constituée de deux compartiments disjoints alimentés chacun en gaz réactifs dioxygène et dihydrogène. Les deux électrodes sont séparées par l’électrolyte, solution qui laisse circuler les ions. Du platine est inséré dans les deux électrodes poreuses.
1.1) Pour cette pile acide, les équations des réactions aux électrodes s’écrivent :
H2 (g) = 2 H+(aq) + 2 e–
O2 (g) + 4 H+(aq) + 4 e– = 2 H2O(l)
Des deux gaz réactifs préciser quel est le réducteur et quel est l’oxydant. Justifier la réponse.
Montrer que l’équation de la réaction globale de fonctionnement s’écrit :
2 H2 (g) + O2 (g) = 2 H2O(l)
1.2) Pour l’environnement quel est l’avantage d’une pile à combustible utilisant
le dihydrogène par rapport à un carburant classique ?
1.3) Des électrodes 1 ou 2, quelle est celle appelée « cathode » ? Justifier.
1.4) Indiquer sur le schéma le sens de circulation des électrons. En déduire
à quelle électrode correspond le pôle positif de la pile et à quelle électrode
correspond le pôle négatif.
1.5) Le platine inséré dans les deux électrodes poreuses joue le rôle de catalyseur.
Définir un catalyseur.
1.6) Une cellule élémentaire fonctionne pendant une durée Dt =
192 h et débite un courant d’intensité considérée constante I = 300 A. En
utilisant les équations des réactions se produisant aux électrodes, calculer
la quantité de matière de chacun des gaz réactifs nécessaire au fonctionnement
d’une cellule élémentaire.
On donne la constante d’Avogadro NA = 6,02.1023 mol-1 , la charge électrique élémentaire
e = 1,6.10 –19 C.
2 ) Principe de production du dihydrogène par électrolyse au laboratoire :
Une pile à combustible, pendant les phases de production, doit être alimentée en continu par du combustible, la plupart du temps du dihydrogène, et en comburant, le plus souvent du dioxygène, présent à près de 20 % dans l’air ambiant.
Le dihydrogène n’est pas une source d’énergie naturelle. Il faut produire du dihydrogène en émettant le moins de pollution possible. Plusieurs possibilités sont étudiées : à partir de carburants fossiles, de biomasse, d’algues vertes ou de bactéries, de l’électrolyse de l’eau. L’électrolyse peut se concevoir comme un moyen de production simple mais coûteux.
2.1) Au laboratoire on peut produire du dihydrogène en électrolysant une solution aqueuse de sulfate de sodium de concentration molaire en soluté apporté c = 1,0 mol.L-1.
Pour obtenir cette solution, on dissout le sulfate de sodium Na2SO4 (s) dans de l’eau distillée.
Le volume de solution obtenue est V = 500 mL.
2.1.1) Ecrire l’équation de la réaction de dissolution du sulfate de sodium solide.
2.1.2) Compléter littéralement, en fonction de c, V et xf , le tableau descriptif de l’évolution du système au cours de la transformation chimique reproduit dans l'annexe, à rendre avec la copie.
2.1.3) Sachant que dans l’état final de la transformation la quantité de matière d’ions sodium obtenue est de 1,0 mol en déduire l’avancement final de la réaction.
La transformation est-elle totale ?
2.2) Donner l’expression du quotient de réaction Qr, f dans l’état
final du système. Calculer sa valeur.
2.3) On réalise le montage schématisé ci-dessous :
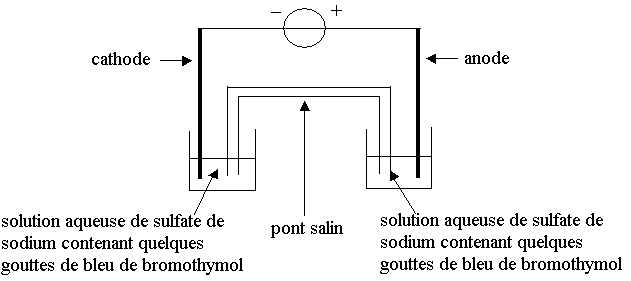
Deux petits cristallisoirs sont remplis de la solution aqueuse de sulfate
de sodium précédente à laquelle on a ajouté quelques gouttes de bleu de bromothymol.
Ils sont reliés l’un et l’autre par un pont salin. Les deux électrodes, respectivement
dans chacun des deux cristallisoirs, sont reliées à un générateur de tension.
Avant de mettre en fonctionnement le générateur, on observe que les deux solutions
contenues dans les cristallisoirs sont vertes. Une fois l’électrolyse lancée,
on observe que les solutions contenues dans les cristallisoirs prennent des
teintes différentes.
On donne pour le bleu de bromothymol : zone de virage : 6,0 – 7,6 ; teinte jaune pour la forme acide ; teinte bleue pour la forme basique.
Les deux réactions ayant lieu aux électrodes ont pour équations :
2 H2O(l) = O2 (g) + 4 H+(aq) + 4 e–
2 H2O(l) + 2 e– = H2 (g) + 2 HO– (aq)
2.3.1) Quelle est la réaction qui a lieu à l’anode ?
Quelle est la réaction qui a lieu à la cathode ?
2.3.2) Quelle couleur prend la solution du côté de la cathode ? du côté de l’anode ?
2.3.3) Ecrire l’équation de réaction qui a lieu lors de l’électrolyse.
2.3.4) L’électrolyse terminée on transvase dans un becher les deux solutions contenues dans chacun des cristallisoirs.
Théoriquement, quelle sera la teinte finale de la solution obtenue ? Justifier par un raisonnement qualitatif à l’aide des quantités de matière.
En fait le dioxyde de carbone dissous dans l’eau distillée peut modifier la teinte théorique attendue.
Annexe
Tableau
|
Equation de la réaction |
Na2SO4 (s) = + |
|||
|
Etat du système |
Avancement (en mol) |
Quantités de matière (en mol) |
||
|
Etat initial |
0 |
|||
|
Etat au cours de la transformation |
x |
|||
|
Etat final |
xf |
|||
©Sciences Mont Blanc
Nouvelle Calédonie Mars 2005 - III ) Oscillateur solide-ressort
:
Le but de cet exercice est de vérifier l’accord entre l’expérience et la théorie dans le cas des oscillations libres d’un système solide-ressort horizontal.
Etude expérimentale :
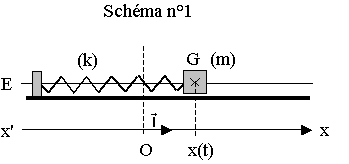
Au laboratoire on filme, avec une caméra numérique, les oscillations libres d’un solide de masse m. Ce solide est attaché à deux ressorts identiques à spires non jointives, de constante de raideur k1, et il est posé sur un banc à coussin d’air horizontal (figure 1).
m = 54,0 g, la masse des ressorts est négligeable et k1 = 12,0 N.m–1.
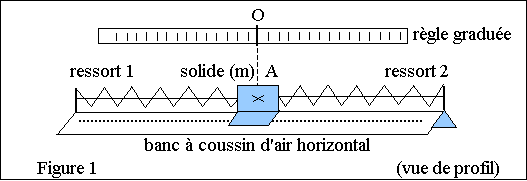
Les deux ressorts restent tendus pendant toute l’expérience. Une règle graduée horizontale est placée à la verticale au dessus du banc. Lorsque le système solide-ressorts est en équilibre, la soufflerie du banc étant en fonctionnement, le point A repéré sur le solide est à la verticale du zéro de la règle graduée (figure 1).
On écarte alors le solide vers la gauche et on l’abandonne sans vitesse initiale.
Le point A oscille entre les positions B et C ; on filme les oscillations (figure 2).
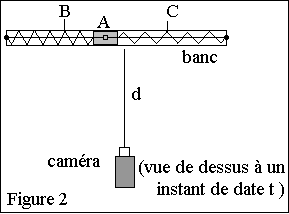 La fréquence d’enregistrement des images est égale à
25 images par seconde. La caméra est placée dans le même plan horizontal que
le banc, à une distance d de celui-ci, grande devant la distance BC. Son axe
optique (ou axe de visée) en pointillés sur la figure 2 est perpendiculaire
au banc et passe par A lorsque le système est à l’équilibre.
La fréquence d’enregistrement des images est égale à
25 images par seconde. La caméra est placée dans le même plan horizontal que
le banc, à une distance d de celui-ci, grande devant la distance BC. Son axe
optique (ou axe de visée) en pointillés sur la figure 2 est perpendiculaire
au banc et passe par A lorsque le système est à l’équilibre.
Un logiciel approprié permet de pointer les différentes positions du point A sur l’écran vidéo entre ses deux positions extrêmes B et C.
On commence le pointage un peu avant le premier passage du point A à la verticale du point O et on le poursuit un peu après son troisième passage à la verticale du point O.
Le fichier de données est transféré vers un tableur qui permet de modéliser et d’afficher la courbe x = f(t), x étant l’abscisse du point A par rapport à l’origine O.
On obtient le graphe n°1 de l’annexe (à rendre avec la copie).
L’origine des dates t = 0 s correspond au passage du point A à la première position enregistrée.
1 ) Etude théorique du mouvement du solide
Dans cette étude tous les frottements sont négligés.
On peut modéliser un oscillateur mécanique horizontal par un système solide-ressort constitué d’un solide de masse m, fixé à l’extrémité d’un seul ressort à spires non jointives, de masse négligeable et de constante de raideur k.
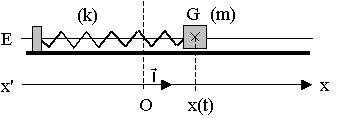
La position du centre d’inertie G du solide est étudiée dans un référentiel terrestre considéré comme galiléen et repérée par son abscisse x(t) sur un axe horizontal x’Ox.
L’origine des abscisses correspond à l’abscisse de G lorsque le solide est à l’équilibre.
Le solide est mis en oscillation. La période propre des oscillations est T0.
1.1) Forces exercées sur le solide en mouvement.
1.1.1) On note F la force exercée par le ressort sur le solide.
Pour une position quelconque du solide, nommer les trois forces qui s’exercent sur ce solide. Les représenter au centre d’inertie G, sans souci d’échelle, sur le schéma n°1 de l’annexe à rendre avec la copie.
1.1.2) En rappelant l’expression du vecteur force F en fonction de l’allongement algébrique x, vérifier mathématiquement que cette force a bien le sens attendu lorsque le centre d’inertie G se trouve à droite de la position d’équilibre sur le schéma n°1 de l’annexe à rendre avec la copie.
1.2) Equation différentielle du mouvement du solide.
1.2.1) En appliquant la deuxième loi de Newton au solide, établir l’équation différentielle du mouvement de son centre d’inertie G.
1.2.2) Sachant que la solution générale de l’équation différentielle est de la forme :
x(t) = Xm . cos [(2p/T0).t + j0]
montrer que l’expression de la période propre T0
de l’oscillateur est : T0 = 2p ![]() (m/k) .
(m/k) .
1.2.3) Vérifier l’homogénéité de l’expression de la période propre T0 par une analyse dimensionnelle.
2 ) Retour à l’expérience :
On rappelle qu’il est équivalent dans cette étude de considérer le mouvement d’un point A quelconque repéré sur le solide en translation ou celui du centre d’inertie G du solide.
2.1) Représenter les grandeurs expérimentales T0exp et Xm,exp par des segments en trait épais sur chacun des deux axes de la courbe x = f(t) (graphe n°1 de l’annexe à rendre avec la copie).
2.2) Déterminer les valeurs expérimentales de l’amplitude Xm,exp
et de la période propre T0exp des oscillations du mouvement du
solide à partir du résultat de la modélisation de la courbe donnée dans l'annexe
à rendre avec la copie. Justifier.
2.3) Les deux ressorts de constante de raideur k1 sont équivalents
à un seul ressort de raideur k = 2k1. L’expression de la période propre T0
trouvée dans l’étude théorique reste valable dans le cas de deux ressorts
initialement tendus.
Calculer à partir des résultats de l’étude théorique la période propre T0 des oscillations.
2.4) Comparer les deux valeurs de la période propre en calculant l’écart relatif
½T0exp-T0½/ T0
3 ) Aspect énergétique en l’absence de frottements :
Le système solide-ressort est toujours supposé osciller sans frottement.
Dans le modèle d’oscillateur adopté, le choix des états de référence est tel que :
· l'énergie potentielle de pesanteur est nulle à l’altitude du centre d’inertie G ;
· l'énergie potentielle élastique est nulle lorsque l’allongement du ressort est nul.
3.1) Rappeler l’expression de l’énergie mécanique Em du système solide-ressort horizontal dans le champ de pesanteur à la position d’abscisse x quelconque, en fonction de m, k, x et v la valeur de la vitesse du centre d’inertie G dans le référentiel terrestre.
3.2) Soit Vm la valeur maximale de la vitesse atteinte par le centre
d’inertie G pour les oscillations d’amplitude Xm étudiées.
En traduisant la propriété de l’énergie mécanique donnée au 3.1), montrer que :Vm = 2p.Xm/ T0
3.3) Calculer la valeur de la vitesse maximale du mobile pour une amplitude
de 4,3 cm et une période propre de 0,30 s.
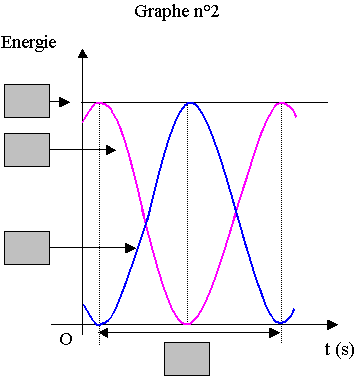
3.4) En vous aidant du graphe n°1, indiquer dans les cases grisées du graphe
n°2 de l'annexe à rendre avec la copie :
· la durée désignée par la double flèche, en fonction de T0 ;
· les énergies : Em, EP (énergie potentielle élastique) et EC (énergie cinétique).
4 ) Aspect énergétique en présence de frottements :
Le système solide-ressort est toujours supposé osciller, mais désormais on tient compte des frottements.
4.1) De quel régime s’agit-il dans le cas où l’on observe toujours des oscillations bien que l’on ne puisse plus négliger les frottements ? Comment nomme-t-on le temps caractéristique T correspondant ?
4.2) Soit Em0 la valeur de l’énergie mécanique de l’oscillateur
lâché sans vitesse initiale avec un allongement maximum initial Xm0.
4.2.1) Etablir l’expression de l’énergie mécanique Em0 en fonction de l’allongement maximum initial Xm0.
4.2.2) On constate expérimentalement qu’au bout d’une oscillation, l’amplitude du mouvement est divisée par r (nombre réel positif non nul).
Etablir l’expression du rapport de l’énergie mécanique correspondante Em1 à l’énergie mécanique initiale Em0 en fonction de r.
Annexe (à rendre avec la copie)
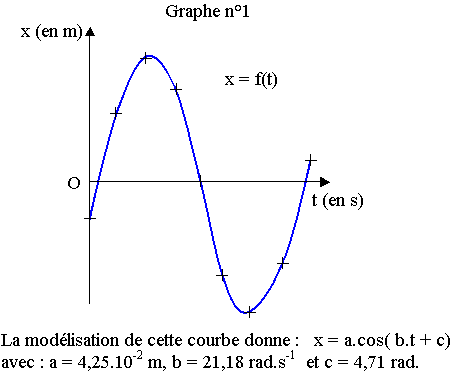
©Sciences Mont Blanc
Nouvelle Calédonie Mars 2005 - I ) (spe)La
lunette de Kepler :
L’importance des observations réalisées par Galilée à l’aide de la lunette
conduit Kepler à rédiger, en 1610, le premier traité moderne d’optique,
le Dioptricae.
Le point central du Dioptricae est l’étude des phénomènes liés aux lentilles. A l’aide de l’optique géométrique, Kepler explique comment on agrandit ou réduit une image grâce à un choix judicieux de lentilles. Il décrit la lunette galiléenne mais propose un nouveau montage utilisant deux lentilles convergentes.
Une lunette de Kepler, appelée aussi lunette astronomique est constituée de deux lentilles minces convergentes, d’axe optique commun (D). Une modélisation de cette lunette est constituée de la manière suivante :
· l’objectif (L1) est une lentille convergente de distance focale f1' = 250 mm, de diamètre D = 25 mm, de centre optique O1 ;
· l’oculaire (L2) est une lentille de distance focale f2' = 50 mm, de centre optique O2.
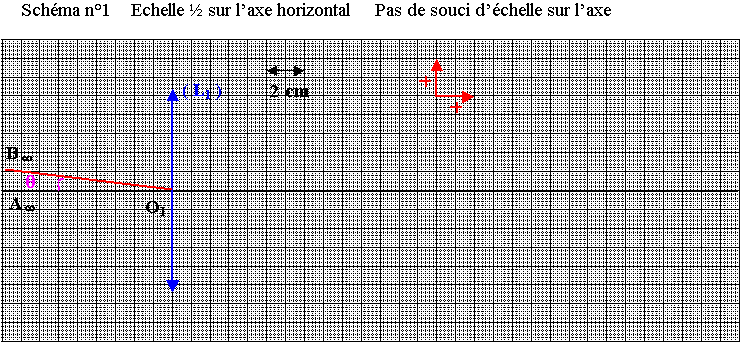
1 ) Schéma de la lunette :
Compléter le schéma n°1 reproduit à l’échelle ½ sur l’axe horizontal, de l'annexe à rendre avec la copie en plaçant la lentille (L2) de telle façon que le foyer objet F2 de l’oculaire coïncide avec le foyer image F’1 de l’objectif.
2 ) Images et grossissement :
L’astre observé est à l’infini, son diamètre AB est perpendiculaire à l’axe optique en A. Tous les rayons issus de B sont parallèles entre eux et font avec l’axe optique un angle q qui est le diamètre apparent de l’astre. Un des rayons issu de B est représenté sur les schémas de l'annexe à rendre avec la copie.
2.1) L’objectif (L1) donne, de l’astre observé, une image A1B1.
Sur le schéma n°1 de l'annexe à rendre avec la copie, construire l’image A1B1 en justifiant la méthode choisie.
2.2) Où se forme l’image définitive A2B2 donnée par l’oculaire (L2) ? Justifier la réponse.
2.3) Compléter la figure en traçant le rayon émergeant de la lunette correspondant au rayon incident tracé issu de B. Justifier les tracés nécessaires à cette construction.
2.4) On appelle grossissement G d’un instrument d’optique le rapport G = q' / q.
q’ est l’angle sous lequel on voit l’image donnée par l’instrument.
q est l’angle sous lequel on voit l’objet à l’œil nu.
Pour les angles petits et exprimés en radians, tanq » q.
Après avoir indiqué q’ sur le schéma n°1 de l'annexe à rendre avec la copie, montrer que, pour la lunette de Kepler modélisée à la question 1, le grossissement a pour expression
G = f1'/ f2'.
En déduire la valeur du grossissement de cette lunette.
2.5) L’expérience montre que les plus belles images du ciel s’obtiennent avec des grossissements dont la valeur est inférieure à un nombre N. Ce nombre est identique à la valeur du diamètre D de l’objectif, exprimé en millimètre, soit ici 25. L’idéal pour l’instrument étudié ici est de disposer d’une gamme d’oculaires permettant des grossissements de N / 7 à N.
A partir d’un grossissement égal à N les images paraissent floues à l’œil humain.
Déterminer pour l’instrument étudié, les deux valeurs extrêmes de f2' correspondant à ces grossissements.
3 ) Cercle oculaire :
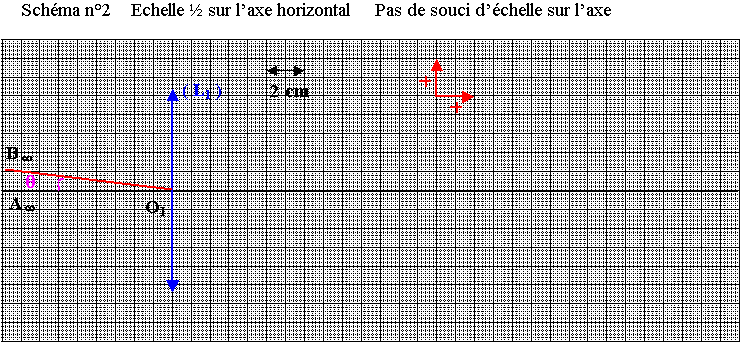
3.1) Définir le cercle oculaire
3.2) Sur le schéma n°2 de l'annexe à rendre avec la copie, construire le cercle oculaire.
Quel est son intérêt pratique ?
4 ) Nouvelle image et grandissement :
On approche l’oculaire de 5 mm vers l’objectif.
4.1) Déterminer, par le calcul, la position de l’image définitive A3B3.
4.2) Calculer le grandissement g de l’oculaire dans ce cas.
Annexe.
©Sciences Mont Blanc