Sujet Bac Pondichéry Mars 2005

Calculatrice autorisée

Pondichéry Mars 2005 - I ) Propriétés de l'acide propanoïque :

On se propose d’étudier deux propriétés chimiques de l’acide propanoïque dans deux parties indépendantes : la réaction de dissolution dans l’eau et la réaction avec l’alcool butan-1-ol.

Données :

Le tableau ci-dessous rassemble quelques propriétés physico-chimiques des réactifs et des produits.

	Formule brute	Masse volumique	Masse molaire	Température d’ébullition
Acide propanoïque	C₃H₆O₂	1,00.10³ kg.m^-3	74,0 g.mol^-1	141,0 °C
Butan-1-ol	C₄H₁₀O	8,10.10² kg.m^-3	74,0 g.mol^-1	117,5 °C
Ester				146,0 °C
Eau				100,0 °C

Dans ce qui suit, l’acide propanoïque est noté AH et l’ion propanoate A^–.

Le conductimètre utilisé permet de mesurer la conductivité σ de la solution étudiée, proportionnelle à sa conductance G.

On considère une solution aqueuse d’acide propanoïque.

On néglige la concentration en ions hydroxyde HO^– par rapport à celles des autres espèces ainsi que leur contribution à la conductivité de la solution.

Dans ces conditions, la conductivité σ de la solution est de la forme :

σ = λ₁.[H₃O⁺] + λ₂.[A^–]

* λ₁ conductivité molaire ionique de l’ion H₃O⁺ : λ₁= 35,0.10^-3 S.m².mol^-1

* λ₂ conductivité molaire ionique de l’ion propanoate : λ₂= 3,58.10^-3 S. m².mol^-1

Ces valeurs sont données à 25 °C et les concentrations [H₃O⁺] et [A^–] sont exprimées en mol.m^-3.

I ) Etude de la réaction entre l’acide propanoïque et l’eau :

On verse 0,10 mole d’acide propanoïque pur dans de l’eau pour obtenir 500 mL d’une solution notée S₀. Pour des mesures de conductimétrie, il est nécessaire de disposer de solutions moins concentrées. On souhaite donc obtenir V = 1,00 L de solution S de concentration 2,0.10^{–
3} mol.L^-1.

1) On donne la liste du matériel disponible : béchers et erlenmeyers de diverses capacités, pipettes jaugées de 10 mL et 20 mL avec son système de pipetage, fioles jaugées de 50,0 mL, 100 mL et 1000 mL. Indiquer le protocole expérimental à suivre pour réaliser la solution S à partir de S₀.

2) Ecrire la formule développée de l’acide propanoïque. On utilisera ensuite les abréviations précisées dans les données.

3) Ecrire l’équation de la réaction chimique entre l’acide propanoïque et l’eau.

4) Dresser un tableau d’avancement de la transformation de 2,0.10^–3 mol d’acide propanoïque dans un volume d'eau tel qu’on obtient V = 1,00 L de solution S.

On notera x_éq l’avancement à l’équilibre.

5) Etablir la relation entre la conductivité s de la solution, les conductivités molaires ioniques λ₁ et λ₂, le volume V et l’avancement x_éq à l’équilibre.

6) La mesure au conductimètre donne σ = 6,20.10^–3 S.m^–1. Déterminer la valeur numérique de x_éq.

En déduire les valeurs numériques des concentrations [A^–]_éq et [H₃O⁺]_éq à l’équilibre.

7) Quelle est la concentration de l’acide propanoïque [AH]_éq à l’équilibre ?

8) Rappeler l’expression de la constante d’acidité K_a du couple acide propanoïque / ion propanoate et la calculer. En déduire le pK_a de ce couple.

II ) Réaction de l’acide avec un alcool :

On prélève 0,20 mole d’acide propanoïque pur et 0,20 mole de butan-1-ol pur qu’on verse dans un ballon.

1) Comment s’appelle la réaction qui a lieu entre ces deux réactifs ?

Ecrire l’équation de cette réaction chimique.

On pourra utiliser les formules brutes (voir le tableau « Données » au début du sujet).

2) Donner le nom des produits formés et leur formule semi-développée.

3) Dresser un tableau d’avancement de la transformation. En déduire l’expression du quotient de réaction Q_r en fonction de l’avancement x à la date t.

4) Calculer l’avancement à l’équilibre x_éq sachant que la constante d’équilibre K = 4,0.

5) En déduire le taux d’avancement t final de la réaction.

6) On demande à un groupe d’élève de formuler des propositions pour augmenter le taux d’avancement. On relève les propositions suivantes :

1 : On chauffe le milieu réactionnel pendant 5 minutes.

2 : On ajoute un catalyseur : l’acide sulfurique concentré par exemple.

3 : On réalise une distillation pour éliminer l’eau.

4 : On chauffe à reflux.

Parmi ces quatre propositions, choisir en justifiant celle qui vous semble correcte.

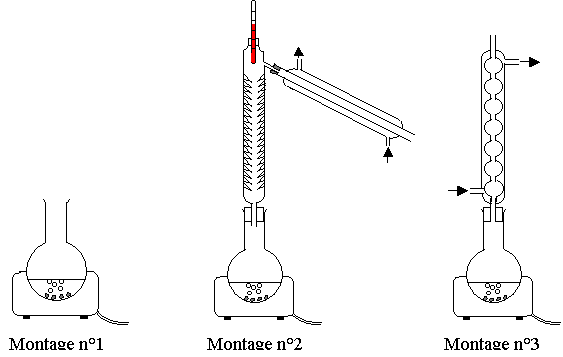
Quel montage réaliserez vous parmi ceux qui sont proposés ci-dessous ?

©Sciences Mont Blanc

Pondichéry Mars 2005 - II ) Mouvement d'un palet :

Les trois parties du problème sont indépendantes.

Les figures 1, 2 et 4 ne sont pas à l’échelle. La figure 3 est à l’échelle 1.

Intensité du champ de pesanteur au niveau du sol : g = 9,80 m.s^-2.

Un palet en acier de masse m = 50,0 g peut se déplacer sur une gouttière inclinée d’un angle

α = 28,0° avec l’horizontale. En D, le palet passe avec une vitesse v_D acquise à l’aide d’un propulseur à ressort. En F, la gouttière est ouverte et le palet peut en sortir librement. Il tombe ensuite dans une éprouvette contenant de la glycérine.

On peut considérer les frottements comme négligeables dans les parties 1 et 2, lorsque le palet glisse dans la gouttière.

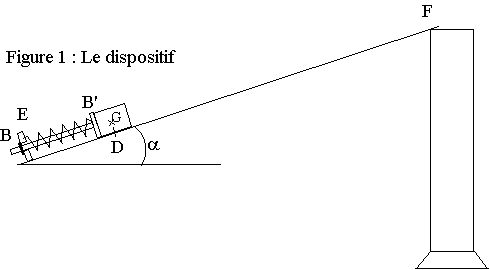
Partie 1 : propulsion du palet

Dans le bas de la gouttière se trouve un dispositif de propulsion constitué d’une tige munie de deux butées B et B’ servant d’axe à un ressort. Le dispositif a une masse négligeable devant celle du palet. Le ressort a une longueur à vide l₀.

L’extrémité E du ressort est maintenue fixe, l’autre est libre et reste en contact avec le palet par l’intermédiaire de la butée B’ tant que le ressort est comprimé.

La position du centre d’inertie G du palet est repérée sur un axe x’x de même direction que la ligne de plus grande pente de la gouttière et orienté vers le haut (voir figure 2).

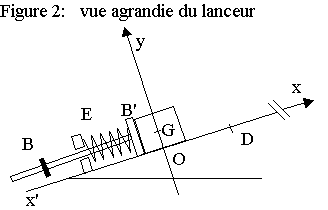
Un manipulateur tire sur la tige et comprime ainsi le ressort jusqu’à ce que le centre d’inertie du palet se trouve au point O. En lâchant la tige, il libère le dispositif qui propulse le palet.

Lorsque le centre d’inertie du palet arrive en D, la butée B bloque le mouvement du ressort qui retrouve dans cette position sa longueur à vide et libère le palet

On filme le mouvement du palet puis on exploite la vidéo avec un logiciel adapté.

La figure 3 suivante, présente la position qu’occupe le centre d’inertie G du palet à intervalles de temps réguliers τ = 20,0ms (points G₀ à G₅) A t = 0, le centre d’inertie du palet est au point O ou G₀

1) En exploitant numériquement la figure 3, déterminer les vitesses v_G2 et v_G4 du palet aux points

G₂ et G₄.

2) Exprimer le vecteur accélération a_G3 du palet au passage du point G₃ en fonction des vitesses

v_G4 et v_G2 et de l’intervalle de temps τ.

En déduire la valeur de cette accélération a_G3.

3) Faire l’inventaire des forces qui s’appliquent au palet et les représenter sur un schéma.

4) En projetant la seconde loi de Newton appliquée au palet sur l’axe x'x, exprimer la valeur de la force de rappel F du ressort en fonction de m, g, a_G , α.

5) A partir du résultat de 2) et des mesures, calculer la valeur de F au point G₃.

Partie 2 : Montée du palet dans la gouttière :

Le palet n’est plus sous l’action du propulseur et il quitte le point D avec une vitesse v_D= 2,00 m.s^-1 puis il glisse jusqu’au point F où il s’arrête.

Dans cette partie du mouvement, on prendra la position du centre d’inertie du palet en D comme origine des altitudes (z_D = 0) et comme niveau de référence de l’énergie potentielle de pesanteur : E_PP(D) = 0.

1) Faire l’inventaire des forces qui s’appliquent au palet sur le trajet DF et les représenter sur un schéma.

2) Donner l’expression au point D de l’énergie mécanique E_M(D) du palet en translation dans le champ de pesanteur.

3) Donner l’expression de l’énergie mécanique E_M(F) du palet au point F, en fonction de m, g, α et de la distance DF.

4) Montrer que sur le trajet DF, l’énergie mécanique du palet en translation dans le champ de pesanteur se conserve. En déduire la valeur de la distance DF.

Partie 3 : Chute du palet sans vitesse initiale.

En F, le palet poursuit son mouvement en réalisant une chute verticale (sans vitesse initiale) dans une éprouvette contenant de la glycérine (voir figure 4 page suivante). On admettra que dans ce cas, le palet est soumis à une force de frottement fluide, modélisée par un vecteur f de même direction que le vecteur vitesse v mais de sens opposé et de valeur f = k.v, k étant une constante positive.

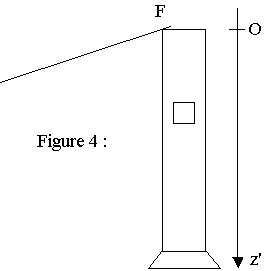
1) Faire l’inventaire des forces qui s’appliquent sur le palet pendant sa chute dans la glycérine et les représenter sur un schéma.

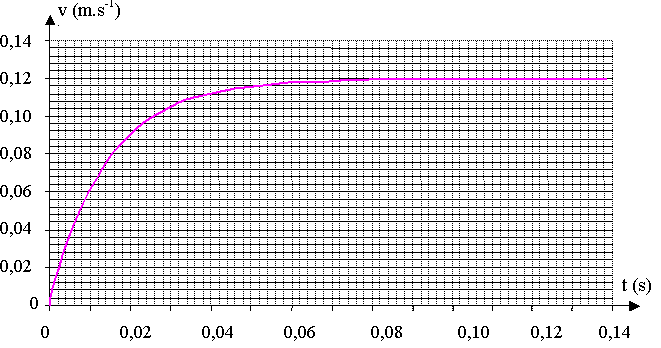
2) En appliquant la seconde loi de Newton, montrer que le mouvement du centre d’inertie du palet obéit à une équation différentielle du type : dv/dt = A – B.v.

Donner les expressions littérales de A et B en fonction des données du texte, de la masse volumique ρ de la glycérine et du volume V₀ du palet.

3) En utilisant le graphe v = f(t) suivant, calculer numériquement les valeurs de A et B en justifiant votre démarche.

©Sciences Mont Blanc

Pondichéry Mars 2005 - III ) Etude d'un circuit RL :

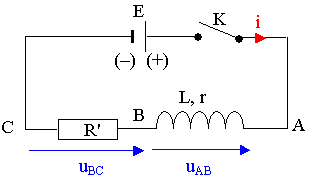
Un circuit électrique comporte, placés en série : un générateur idéal de tension continue de f.é.m. E = 6,00 V, un interrupteur K, une bobine d’inductance L et de résistance r = 10,0 W et un conducteur ohmique de résistance R = 200 W.

Un ordinateur relié au montage par une interface appropriée permet de visualiser au cours du temps les valeurs des tensions u_ABet u_BC.

Le schéma du circuit ci-dessous précise l’orientation du circuit et les tensions étudiées.

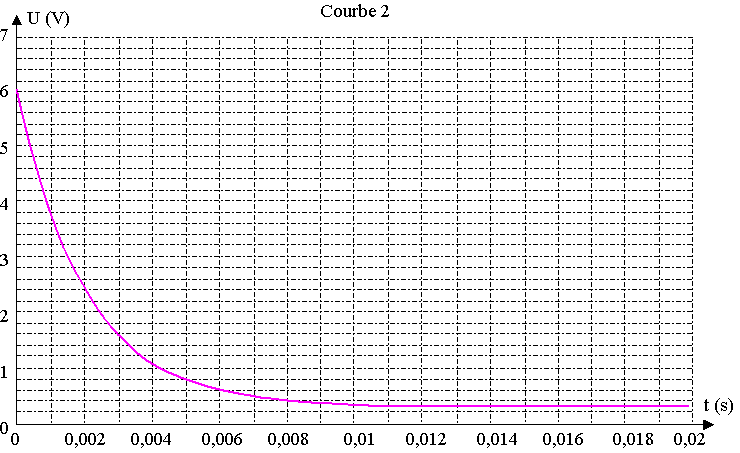
A t = 0, on ferme l’interrupteur K et on procède à l’acquisition. On obtient les deux courbes suivantes, notées courbe 1 et courbe 2.

1) Etude du montage.

1.1) A défaut d’ordinateur et d’interface d’acquisition, quel type d’appareil peut-on utiliser pour visualiser le phénomène étudié ?

1.2) Donner l’expression de u_AB en fonction de i et de di/dt.

1.3) Donner l’expression de u_BC en fonction de i.

1.4) Associer les courbes 1 et 2 aux tensions u_AB et u_BC. Justifier.

2) Détermination de l’intensité du courant en régime permanent.

2.1) Appliquer la loi d’additivité des tensions pour déterminer l’expression I₀ de l’intensité du courant qui traverse le circuit lorsque le régime permanent est établi. Calculer la valeur de I₀.

2.2) Exploiter l’une des deux courbes pour retrouver cette valeur de I₀.

3) Calcul de l’inductance L de la bobine.

3.1) Exploiter l’une des deux courbes pour déterminer la constante de temps t du montage. Expliciter votre méthode.

3.2) Rappeler l’expression de la constante de temps t en fonction des grandeurs caractéristiques du circuit. Montrer que cette expression est homogène à un temps.

3.3) A partir de la valeur de t mesurée, calculer l’inductance L de la bobine.

Pondichéry Mars 2005 - III ) Etude d'un son et de sa réception avec un récepteur radio (spécialité) :

On se propose, dans cet exercice, d’étudier dans une première partie le son produit par une corde métallique vibrant entre deux points fixes A et B puis, dans une deuxième partie, la transmission et la réception de ce son par ondes hertziennes.

Données :

La fréquence propre f₀ d’un circuit L, C est donnée par la relation L . C . (2p f₀)² = 1

Première partie : étude du son :

On a enregistré, à l’aide d’un microphone et d’un oscilloscope, le signal électrique correspondant au son produit par la corde vibrante.

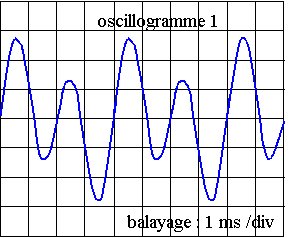On a obtenu l’oscillogramme ci-contre :

1.1) Le son produit est-il complexe ? Justifier.

1.2) Déterminer la valeur de la fréquence f₁ du son fondamental.

Déterminer la valeur de la fréquence f₃ de l’harmonique de rang 3.

1.3) Un générateur basses fréquences fait circuler dans cette corde métallique un courant alternatif sinusoïdal de fréquence réglable. La corde passe entre les pôles d’un aimant en U.

Représenter sur un schéma l’état vibratoire de la corde entre A et B pour le fondamental puis pour l’harmonique de rang 3.

1.4) Donner la relation entre la longueur d’onde l, la longueur AB et le rang n de l’harmonique.

1.5) La longueur AB vaut 0,90 m. En déduire la célérité V des ondes le long de la corde.

Deuxième partie : Emission et réception

On étudie un dispositif expérimental émetteur-récepteur d’ondes pour transmettre le son précédent par voie hertzienne. L’émetteur utilise une onde porteuse de fréquence f, modulée en amplitude par le signal électrique de fréquence f₁ correspondant au son de la première partie. La tension modulée u_m émise par l’émetteur est représentée en annexe sur les deux premiers graphes.

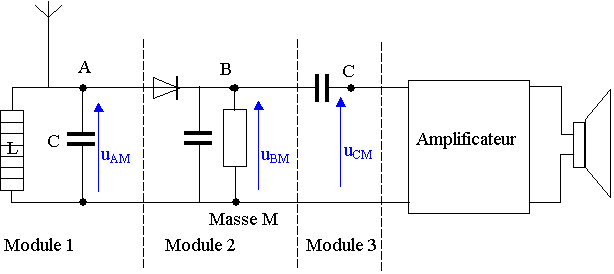
Le récepteur constitué de 3 modules notés 1,2 et 3 selon le schéma de principe ci-après.

Les tensions correspondantes sont représentées en annexe (graphes G1, G2 et G3).

2.1) En utilisant la partie zoomée de la tension modulée u_m à la sortie de l’émetteur (2^ème graphe figurant en annexe), déterminer la fréquence f de la porteuse.

2.2) Le module 1 du récepteur, filtre passe bande ou circuit d’accord, est composé d’une bobine d’inductance L de valeur fixe et d’un condensateur de capacité C réglable.

2.2.1) Quel est le rôle de ce module ?

2.2.2) Quel est l’intérêt de pouvoir faire varier la capacité ?

2.2.3) A quelle valeur doit-on fixer C si L = 1,00 mH ?

2.3) Les graphes des tensions u_AM, u_BM , u_CM sont représentées en annexe. Attribuer les graphes
numérotés G1, G2, G3 aux tensions u_AM, u_BM , u_CM en justifiant brièvement vos choix.

Annexe de l'exercice III (Spécialité)

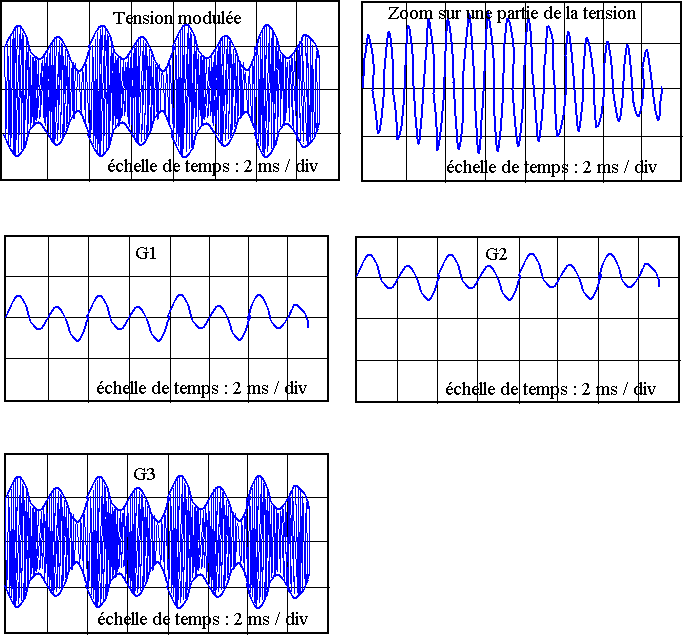
Pour chaque oscillogramme, la trace correspondant à une tension nulle est confondue avec l’axe horizontal central.