Sujet Bac Réunion Juin 2006
Calculatrice autorisée
I ) La pile cuivre aluminium et le condensateur (8 points)
II ) Le parfum de poire (4 points)
III ) Propagation d'une onde (4
points)
I ) Produire un son (spe) (4 points)
Réunion Juin 2006 - I ) La pile cuivre aluminium et
le condensateur :
Les questions IV , V .et VI peuvent être résolues indépendamment les unes des autres et indépendamment de la résolution des questions I, II et III.
La pile cuivre - aluminium
1 ) On introduit dans un bécher un volume V = 50 ml d'une solution de chlorure d'aluminium (Al3+ + 3 Cl-), de concentration en soluté apporté 0,10 mol.L-1 , dans laquelle plonge une lame d'aluminium. Dans un .second bécher, on introduit un volume V = 50 ml d'une solution de sulfate de cuivre (Cu2+ + SO42- ), de concentration molaire en soluté apporté 0,10 mol.L-1, dans laquelle plonge une lame de cuivre. On relie les deux béchers à l'aide d'un pont salin contenant du nitrate d'ammonium (NH4+ + NO3-) .
Lorsqu'on branche un voltmètre électronique avec sa borne COM reliée à l'électrode d'aluminium, on mesure une différence de potentiel U = + 1,8 V.
1.1) Quelle est la polarité de la pile ?
1.2) Quel est le rôle du pont salin ?
2 ) On relie la pile à un conducteur ohmique.
2.1) Faire un schéma légendé en indiquant le sens du courant dans le circuit, et en représentant le déplacement des différents porteurs de charge à l'intérieur et à l'extérieur de la pile.
2.2) Écrire et nommer les réactions qui se produisent aux électrodes.
2.3) Montrer que la transformation entre les deux. couples peut s'écrire :
3 Cu2+ + 2 Al = 3 Cu + 2 Al3+
2.4) La constante d'équilibre associée à la transformation est K= 1020.
2.4.1) Calculer le quotient de réaction initial.
2.4.2) Montrer en appliquant le critère d'évolution spontanée que le sens
d'évolution est cohérent avec le fonctionnement de la pile,
3 ) La pile fonctionne pendant 1 h 30 min en débitant un courant d'intensité
constante I =40 mA.
Données : Le faraday : valeur absolue de la charge d'une mole d'électrons
de symbole F.
F = 9,65.104 C.mol-1
Masse molaire de l'aluminium : 27 g.mol-1 .
3.1) Calculer la quantité d'électricité Q échangée pendant 1 h30 min.
3.2) Calculer la quantité de matière d'électrons ne échangée pendant
cette durée.
3.3) Donner la relation entre ne et nal , quantité de
matière d'aluminium ayant disparu .
3.4) Calculer la perte de masse de l'électrode d'aluminium.
 4 ) La pile est équivalente
à l'association série d'un générateur de tension de force électromotrice E
= 1,8 V et d'un conducteur ohmique de résistance r.
4 ) La pile est équivalente
à l'association série d'un générateur de tension de force électromotrice E
= 1,8 V et d'un conducteur ohmique de résistance r.
On remplace la conducteur ohmique par un condensateur branché entre les bornes P et M de la pile (voir schéma ci-après).
4.1) Recopier le schéma ci- dessus sur la copie en représentant :
- le sens du courant au cours de la charge du condensateur.
- les flèches représentant des tensions uQM , uQP et uAB .
4.2) Quel est le signe de la charge prise par l'armature A du condensateur
au cours de la charge ?
4.3) À chaque instant, la charge qA de l'armature A du condensateur
est proportionnelle à la tension uAB entre ses armatures A et B.
Quels sont le nom et l'unité de ce coefficient de proportionnalité ?
5 ) Étude de la variation de la. tension
aux bornes du condensateur au cours du temps lorsqu'il est soumis à un échelon
de tension.
5.1) À l'aide d'un graphique, expliquer ce qu'est un échelon de tension E.
5.2) L'équation différentielle permettant de déterminer la tension uAB
aux bornes du condensateur est de la forme :
E = r .C.duAB/dt + uAB
5.2.1). Que représente la grandeur C ?
5.2.2) La solution de cette équation différentielle est : uAB =
E . (1 – e – t / t). En déduire l'expression de la constante t.
5.2.3) Quelle est l'unité de t ? Le vérifier par analyse
dimensionnelle. Quel nom donne-t-on à t ?
5.2.4) Quelles valeurs, écrites en fonction de E, prend la tension uAB aux dates suivantes :
t = t t = 3 t t = 5 t t = 10 t ?
5.2.5) À partir de ces résultats, dessiner l'allure de la courbe uAB
= f (t) de t = 0 à environ t = 6 t.
6 ) Après avoir chargé un condensateur de capacité C = 100 mF sous la tension
E = 1,8 V, on le décharge dans un moteur qui en tournant provoque la montée
d'une hauteur h, à vitesse constante, d'un solide S de masse m = 100 g.
Donnée : g = 10 m.s-2 .
6.1) Quelle est l'énergie maximale e emmagasinée dans le condensateur ?
6.2) De quelle hauteur h pourrait monter le solide si le transfert d'énergie
se faisait avec un rendement de 100 % ?
©Sciences Mont Blanc
Réunion Juin 2006 - II ) Le parfum de poire
:
L'éthanoate de pentyle ou parfum de poire est plus connu sous le nom d'acétate d'amyle. Il peut être obtenu par réaction de l'acide acétique avec l'alcool amylique, alcool extrait jadis de la pomme de terre, tubercule riche en amidon.
La formule semi-développée est :

1 ) Étude théorique
1.1) Nommer la fonction chimique présente dans cette molécule.
1.2) L'éthanoate de pentyle peut être obtenu à partir de deux réactifs A et
B.
1.2.1) Le réactif A est l'acide carboxylique.
Quelle est la fonction organique que contient le réactif B ? Écrire sa formule semi-développée.
1.2.2) Écrire l'équation de la réaction chimique conduisant à la formation
de la molécule d'éthanoate de pentyle.
1.2.3) Nommer les réactifs A et B dans la nomenclature officielle ainsi que
l'autre produit formé au cours de cette synthèse.
1.2.4) Quel est le nom de cette synthèse ?
2 ) Étude cinétique
2.1) Décrire un méthode opératoire permettant de suivre l'évolution de la quantité de matière du réactif A au cours du temps.
2.2) À un instant t = 0 s , on mélange 0,50 mol de réactif A et 0,50 mol de
réactif B identifiés à la question 1.2.1. On ajoute une petite quantité d'acide
sulfurique.
Le milieu réactionnel est maintenu à une température constante de 25°C et le volume total du mélange réactionnel est V= 83 mL.
2.2.1) Quel est le rôle de l'acide sulfurique ?
2.2.2) L'acide sulfurique intervient-il dans l'équation de la réaction ?
2.3) On détermine, toutes les 5 minutes, la quantité n de matière d'éthanoate
de pentyle formée. Les résultats obtenus sont rassemblés dans le tableau ci-dessous
:
|
Temps en min |
0 |
5 |
10 |
15 |
20 |
25 |
30 |
35 |
40 |
45 |
50 |
55 |
60 |
|
n en mol |
0,00 |
0,14 |
0,21 |
0,25 |
0,275 |
0,295 |
0,31 |
0,32 |
0,325 |
0,33 |
0,33 |
0,33 |
0,33 |
Les points correspondants sont reportés sur la figure 1 de l'annexe 3 à remettre
avec la copie.
2.3.1.a) Établir un tableau descriptif de l'évolution du système avec l'état
initial, un état intermédiaire et l'état du système à la date t = 60 min.
2.3.1.b) Donner la relation entre la quantité n d'éthanoate de pentyle et
l'avancement x.
2.3.2.a) Définir la vitesse volumique de la réaction de formation de l'éthanoate
de pentyle
2.3.2.b) Comment évolue cette vitesse de réaction au cours du temps ?
Quel facteur cinétique permet d'expliquer cette évolution ?
2.3.2.c) Quel est l'état du système à partir de t = 50 min ?
2.3.3) Définir le temps de demi-réaction t ½ . Le déterminer graphiquement.
2.3.4) On considère maintenant le cas où la synthèse est faite sans ajout
d'acide sulfurique.
2.3.4.a) Comment évolue le temps de demi-réaction par rapport à celui de la question précédente?
2.3.4.b) Tracer sur le graphique de la figure 1, annexe 3 à remettre avec
la copie, l'allure de la courbe représentant l'évolution au cours du temps
de la quantité n d'éthanoate de pentyle lorsqu'il n'y a pas d'ajout d'acide
sulfurique dans le milieu réactionnel.
On précisera l'état final du système.
Annexe 3 ( à remettre avec la copie
)

©Sciences Mont Blanc
Réunion Juin 2006 - III ) Propagation d'une onde :
1 ) Étude sur une cuve à ondes.
On laisse tomber une goutte d'eau sur une cuve à ondes. Le fond de la cuve à ondes présente un décrochement de telle sorte que l'onde créée par la chute de la goutte d'eau se propage d'abord à la surface de l'eau dont l'épaisseur au repos est e1 = 3 mm puis ensuite à la surface de l'eau dont l'épaisseur au repos est e2 = 1 mm. On filme la surface de l'eau à l'aide d'une webcam.
Le clip vidéo est effectué avec une fréquence de 24 images par seconde. Le document 1 (annexe 1) représente les positions du front de l'onde créée par la chute de la goutte d'eau, repérées sur les images n° 1, n° 7, n° 8 et n° 14 du clip.
1.1) Donner les définitions d'une onde transversale et d'une onde longitudinale.
À quelle catégorie appartient l'onde créée par la goutte d'eau sur la cuve à ondes ?
1.2) Calculer la célérité c de cette onde pour les deux épaisseurs d'eau mentionnées
dans le document 1 (annexe 1).
L'échelle de ce document est 1 (1 cm représente 1 cm).
1.3) Comment varie, dans cet exemple, la célérité c de l'onde en fonction
de l'épaisseur de l'eau ?
2 ) Ondes périodiques.
On installe sur la cuve à ondes un vibreur qui permet d'obtenir des ondes planes. La fréquence du vibreur a été fixée à 24 Hz.
Une source lumineuse éclaire la surface de l'eau. Cette lumière traverse l'eau et est captée ensuite par la webcam.
Le document 2 d'échelle 1 (annexe 1) représente l'onde périodique obtenue à partir d'une image du clip vidéo.
2.1) Comment appelle-t-on la distance séparant deux franges brillantes (ou
sombres) successives ?
Quelle relation lie cette grandeur à la célérité c de l'onde et sa période temporelle T ?
2.2) À l'aide du document 2 (annexe 1), calculer la célérité c de l'onde périodique
pour les deux épaisseurs d'eau de 3 et 1 mm.
Quelle est l'influence de l'épaisseur de l'eau sur la célérité de l'onde périodique ?
2.3) On utilise maintenant une cuve à ondes sans décrochement. L'épaisseur
de l'eau au repos est constante. Après avoir fait varier la fréquence du vibreur,
on a réalisé des photographies et on a mesuré la longueur d'onde l pour chacun des enregistrements.
Les résultats ont
été consignés dans le tableau ci-dessous.
|
f (Hz) |
12 |
24 |
48 |
96 |
|
l (m) |
0,018 |
0,0097 |
0,0059 |
0,0036 |
Calculer la célérité c de l'onde périodique pour chaque enregistrement. Comment
évolue cette célérité en fonction de la fréquence de l'onde ?
3 ) Un phénomène caractéristique des ondes.
3.1) Expérience sur les ondes lumineuses.
On place sur un faisceau laser une fente de dimension a = 0,080 mm.
On place après la fente un écran. La distance entre la fente et l'écran est D = 3,00 m, (voir figure 1 document 3 annexe 2).
La figure obtenue sur l'écran est représentée sur la figure 2 document 3 (annexe 2).
3.1.1) Comment se nomme le phénomène observé ?
3.1.2) L'écart angulaire q entre le milieu de la tache centrale et la première extinction vérifie
la relation : q = l / a
Calculer la longueur d'onde de ce faisceau laser (on considérera que cet écart angulaire q est faible et que donc q » tanq si q est exprimé en radians).
3.2) Étude sommaire de la houle.
La houle prend naissance sous l'effet du vent loin des côtes.
Un vent de 65 km.h-1 engendre une houle dont les vagues font 1 mètre de hauteur. Ces vagues sont espacées de 230 mètres.
Une vague remplace la précédente après une durée de 12 secondes.
3.2.1) Calculer la vitesse de déplacement des vagues à la surface de l'océan.
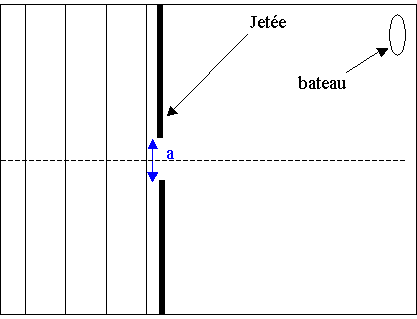
3.2.2) Cette houle arrive sur un port dont l'ouverture entre deux jetées a
une largeur a = 200 m.
Un bateau est stationné au fond du port comme indiqué sur le schéma du document 4.
Ce bateau risque-t-il de ressentir les effets de la houle ?
Justifier la réponse
à l'aide d'un schéma reproduit sur la copie.
Annexe 1
Document 1

Document 2

Document 3

Figure 1 : schéma du dispositif
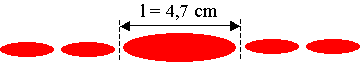
Figure 2 : Figure observée sur l'écran
Document 4
©Sciences Mont Blanc
Réunion Juin 2006 - I ) Produire un son
(spécialité) :
1 ) Onde stationnaire le long d'une corde.
Description du montage (cf. figure n° 1 annexe 1)
Une corde métallique est fixée rigidement à l’une de ses extrémités B. Cette corde passe dans la gorge d'une poulie et on suspend à son autre extrémité une masse m. Cette corde peut vibrer entre le point A et le point B. Elle passe entre les branches d'un aimant en U placé à équidistance de A et B. On relie cette corde aux deux bornes d'un GBF (générateur basse fréquence). Le courant sinusoïdal traversant la corde permet de générer des ondes transversales. Pour des fréquences bien déterminées, des ondes stationnaires apparaissent entre les points A et B. On observe alors un ou plusieurs fuseaux de vibration. Ce montage représenté permet d'étudier les différents paramètres qui influent sur ces ondes stationnaires.
Pour la corde utilisée, on a obtenu un fuseau de vibration pour la fréquence f = 40 Hz.
1.1) Comment appelle-t-on le mode de vibration pour cette fréquence f = 40 Hz ?
1.2) Comment appelle-t-on les autres modes de vibration de la corde ? Quelles sont les valeurs des fréquences qui permettent de les obtenir ?
1.3) Quelle est la relation liant la célérité c, la fréquence f, et la longueur d'onde l de l'onde apparaissant dans la corde ?
1.4) L'onde est stationnaire lorsque la distance parcourue par l’onde lors d'un aller et retour le long de la corde est égale à un nombre entier de longueur d'onde l. Quelle est la relation liant la longueur L de la corde et la longueur d'onde l ?
Etablir la relation liant c, L et f.
1.5) Quelle fréquence doit avoir le courant sinusoïdal pour obtenir deux fuseaux de vibration ?
Où est-il judicieux de placer l'aimant dans ce cas là ?
2 ) Vibration d'une corde de guitare.
Le montage de la figure n°1 (annexe 1) permet de faire varier la tension mécanique F appliquée à la corde.
Le changement de corde permet d'étudier l'influence de la masse linéique.
Une étude complète permet d'établir que les différents modes de vibration d'une corde vérifient la relation :
f = (k / 2 L) . ![]() (F / m)
(F / m)
k est un nombre entier , L : longueur de la corde en m , F : tension mécanique
de la corde en N ,
m : masse linéique de la corde en kg.m-1 , f : fréquence en Hz
Une guitare représentée figure n°2 annexe 2, comporte 6 cordes de masses linéiques
différentes.
Chaque corde est montée entre le chevalet et le sillet, elle est reliée à une clé permettant de régler sa tension (figure n°3 annexe 2).
La distance L entre le chevalet et le sillet est L = 65 cm.
L'une des cordes, dite « corde n°2 », est la corde du La1 de fréquence 110 Hz.
2.1) Quel est l'intérêt de pouvoir régler la tension des cordes ?
2.2) Pourquoi les cordes ont-elles des masses linéiques différentes ?
3.3) Un musicien veut accorder la corde n°2. Avant l'accord, il pince cette corde n°2. On enregistre à l'aide d'un micro le son émis. On obtient l'enregistrement de la courbe 1 (annexe 3)
3.3.1) Quelle est la fréquence de la note émise ?
3.3.2) Un logiciel permet de faire l'analyse spectrale de l'enregistrement précédent.
Les courbes 2 et 3 de l'annexe 3 présentent deux diagrammes de fréquences.
Lequel correspond à l’enregistrement précédent ? Justifier la réponse.
3.3.3) Comment le musicien doit-il agir sur la corde pour obtenir le La 1 ?
Annexe 1
Figure n°1 : montage

Annexe 2
Figure
n°2 : guitare

Figure n°3 : Manche d'une guitare

Annexe 3

Courbe 1 : enregistrement du signal sonore émis par la corde n°2
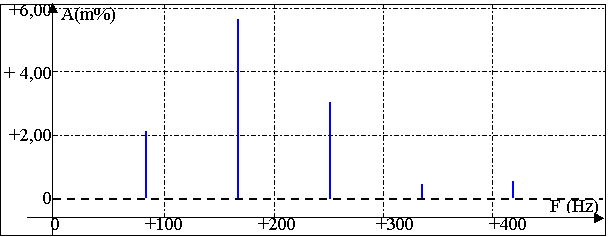
Courbe 2 : Diagramme de fréquences n°1

Courbe 3 : Diagramme de fréquence n°2
©Sciences Mont Blanc