Sujet Baccalauréat France - Juin 2007

Calculatrice interdite

 

Sujet complet en pdf

 

I ) La galiote ( 5,5 points)

II ) Découvertes liées à des éclipses de Soleil ( 6,5 points)

III ) Synthèse d'un ester ( 4 points)

I ) Synthèse d'un conservateur (4 points) (spe)

 

Sujet Bac France - Juin 2007 - I ) La galiote :

 

 

Les parties 1, 2 et 3 de cet exercice sont indépendantes.

Certaines aides au calcul peuvent comporter des résultats ne correspondant pas au calcul à effectuer.

1) Action de la poudre de canon sur le boulet

L’éjection du boulet est provoquée par la combustion de la poudre. Une force de poussée est donc exercée sur le boulet par l’ensemble {galiote + canon + gaz}.

Justifier l’expression soulignée dans le texte encadré ci-dessus, à l’aide d’une des trois lois de Newton. Énoncer cette loi. (On pourra s’aider d’un schéma).

2) La trajectoire du boulet

On souhaite étudier la trajectoire du centre d’inertie G du boulet de masse m. L’étude est faite dans le référentiel terrestre considéré comme galiléen.

Le repère d’étude est (O, , ) et l’origine des dates est choisie à l’instant où le boulet part du point O (voir figure 1 ci-dessous).

Le vecteur vitesse initiale_G du point G est incliné d’un angle α  (appelé angle de tir) par rapport à l’horizontale.

Une fois le boulet lancé, la force de poussée de la partie précédente n’intervient plus.

 

Données :

Volume du boulet : V = 16 dm ³ = 16 L

Masse du boulet : m = 100 kg

Valeur du champ de pesanteur : g = 10 m.s ^{– 2}

Masse volumique de l’air : ρ = 1,3 kg.m ^{– 3}

 

 

 

 

2.1) Inventaire des forces agissant sur le boulet après son lancement

2.1.1) La poussée d’Archimède

Donner l’expression littérale de la valeur F_A de la poussée d’Archimède puis la calculer.

2.1.2) Le poids

Calculer la valeur P du poids du boulet après avoir précisé son expression littérale.

2.1.3) Dans cet exercice, on pourra négliger la poussée d’Archimède devant le poids si la valeur de ce dernier est au moins cent fois plus grande que celle de la poussée d’Archimède. Montrer que l’on est dans cette situation.

2.1.4) Pendant le vol, compte tenu de la masse, de la vitesse et de la forme du boulet, on fait l’hypothèse que les forces de frottement dans l’air sont négligeables devant le poids. En tenant compte de la remarque et des résultats précédents, établir le bilan des forces exercées sur le système {boulet} pendant le vol.

 

2.2) Equation de la trajectoire

Dans toute cette partie, on négligera la poussée d’Archimède et on ne tiendra pas compte des forces de frottement dues à l’air.

2.2.1) En appliquant la deuxième loi de Newton, montrer que les équations horaires du mouvement du point G s’écrivent :

x(t)  = (v₀ .cos α) . t    et    y(t) = - ½ g . t² + (v₀ . sin α) . t

 

2.2.2) Montrer que l’équation de la trajectoire peut se mettre sous la forme y(x) = Ax² + Bx.

On donnera les expressions littérales de A et B et on précisera leurs unités respectives.

 

2.3) Portée du tir

L’équation de la trajectoire du boulet peut se mettre sous la forme y(x) = x × (Ax + B).

Au cours d’un tir d’entraînement, un boulet tombe dans l’eau.

Dans ces conditions, la distance entre le point de départ du boulet et son point M d’impact sur l’eau est appelée portée (voir figure 1 page 2).

On négligera la différence d’altitude entre les points O et M devant les autres distances.

2.3.1) Exprimer la portée d du tir en fonction de A et B.

2.3.2) L’expression littérale de la portée d en fonction de v₀ , α et g est :     d = v₀² . sin 2 α / g

Retrouver, en la justifiant, la valeur α = 45° donnée dans le texte, pour laquelle la portée est maximale, pour une vitesse v₀ donnée.

2.3.3) A partir de la question précédente et des données, calculer la vitesse initiale du boulet pour atteindre la portée maximale donnée dans le texte.

2.3.4) En fait, les frottements dans l’air ne sont pas négligeables.

Avec un angle de tir restant égal à 45°, la vitesse initiale du boulet doit-elle être supérieure ou inférieure à celle trouvée à la question 2.3.3. pour obtenir la même portée maximale ? Justifier sans calcul.

3) Restauration d’un boulet par électrolyse

Un boulet est retrouvé par un archéologue, qui le restaure par électrolyse en solution basique.

Ce procédé a pour but, notamment :

- d’éliminer la gangue (substance qui forme une enveloppe autour d'une autre matière) qui entoure le boulet ;

- de débarrasser l’objet de tous les ions chlorure qui, au contact de l’humidité de l’air et du dioxygène amènent à la formation d’acide chlorhydrique conduisant à la destruction rapide du boulet. Ces ions chlorure sont également présents dans la gangue.

 

Le schéma de principe de l’électrolyse est le suivant :

 

La lente destruction de la gangue libère dans l’électrolyte les ions chlorure qu’elle contenait.

 

L’équation de la réaction modélisant l’électrolyse est :

2 Cl^- (aq) + 2 H₂O (l)  =  Cl₂ (g) + H₂ (g) + 2 HO^- (aq)

 

Les couples d’oxydoréduction mis en jeu sont : Cl₂ (g) / Cl^- (aq)  et  H₂O (l) / H₂ (g)

3.1) La réaction se produisant à l’anode est-elle une oxydation ou une réduction ?

3.2) Ecrire l’équation de la réaction ayant lieu à l’anode.

A quelle borne du générateur est reliée cette électrode ?

3.3) A l’une des électrodes, on observe un dégagement de dihydrogène.

L’équation de la réaction électrochimique associée est :

2 H₂O (l) + 2 e^- =  H₂ (g) + 2 HO^- (aq)    (1)

 

La pression exercée par le dihydrogène permet de décoller la gangue. L’élimination de la gangue se fait sous une intensité I constante et pendant une durée Δt qui dépendent, entre autres, de la nature de l’objet et de son état de corrosion.

 

Données :

Charge élémentaire : e = 1,6 x 10 ^–19 C         Constante d’Avogadro : N_A =  6,0 x 10 ²³ mol ^{– 1}

Intensité du courant : I = 1,0 A                             Durée de l’électrolyse :  Δt = 530 heures

 

On note Q la valeur absolue de la charge électrique totale ayant circulé dans le dispositif pendant la durée Δt de l’électrolyse.

3.3.1) Donner l’expression littérale du nombre N d’électrons transférés et celle de la quantité d’électrons n(e^–) en fonction des grandeurs données.

3.3.2) Pour simplifier, on fait l’hypothèse que la réaction correspondant à l’équation (1) est la seule à se produire au niveau de l’électrode concernée.

En s’aidant éventuellement d’un tableau d’avancement, établir une relation entre la quantité n(H₂) de dihydrogène dégagé et la quantité d’électrons n(e^–) et en déduire que n(H₂) = ½ I . Δt / (e . N_A)

3.3.3) Calculer la valeur de n(H₂).

3.3.4) En déduire quel serait le volume de dihydrogène dégagé dans les conditions de l’expérience.

On donne le volume molaire des gaz dans les conditions de l’expérience : V_M = 24 L. mol ^{– 1} .

 

©Sciences Mont Blanc

 

Sujet Bac France - Juin 2007 - II ) Découvertes liées à des éclipses de Soleil:

 

Cet exercice se compose de deux parties indépendantes.

Certaines aides au calcul peuvent comporter des résultats ne correspondant pas au calcul à effectuer.

A) Partition lunaire

 

1) Ondes créées lors de l’éclipse

1.1) Définir une onde mécanique progressive.

1.2) Définir une onde transversale.

1.3) Dire, en justifiant la réponse, si les ondes créées lors de l’éclipse peuvent être sonores.

 

2) Caractéristiques des ondes créées

L’équipe en charge du projet a pu détecter à faible altitude, une série d’ondes dont la période moyenne est de l’ordre de 10 minutes et la célérité moyenne est de l’ordre de 100 km.h ^{– 1}.

2.1) Vérifier que la fréquence de l’onde est effectivement largement inférieure à 20 Hz.

2.2) Ces ondes peuvent-elles être diffractées par des montagnes séparées par une distance de 10 km ? Justifier la réponse.

 

B) Découverte historique d’un nouvel élément chimique

Données :

Célérité de la lumière dans le vide : c = 2,998 x 10⁸ m.s ^{– 1}

Constante de Planck : h = 6,626 x 10 ^{– 34} J.s

1 eV = 1,602 x 10 ^{– 19} J

Longueur d’onde de la raie D du sodium dans le vide : λ_Na = 589,0 nm.

Longueur d’onde de la raie jaune de l’hélium dans le vide : λ_He = 587,6 nm.

 

1) Spectre d’énergie

1.1) Illustrer, en s’aidant d’un schéma de niveaux d’énergie d’un atome, le phénomène d’émission d’un photon (quantum d’énergie lumineuse).

1.2) On note E l’énergie du photon émis lors d’une transition énergétique d’un atome.

Donner l’expression littérale de E en fonction de la longueur d’onde λ de la radiation lumineuse émise dans le vide, de la constante de Planck h et de la célérité de la lumière dans le vide c.

 

1.3) Raie D du sodium

1.3.1) Calculer la valeur de E en électronvolts, pour le rayonnement correspondant à la raie D du sodium.

1.3.2) Déterminer, en s’aidant de la figure 2 page 7, à quelle transition correspond cette émission.

1.4) L’énergie du photon correspondant à l’émission de la raie jaune de l’hélium (de longueur d’onde λ_He) est égale à 2,110 eV.

En s’aidant de la figure 2 page 7, justifier que cette émission ne peut pas être attribuée au sodium.

 

2) Formation de l’hélium dans le Soleil

Les noyaux d’hélium 3 et d’hélium 4 peuvent être produits par une suite de réactions nucléaires dont les équations sont indiquées ci-dessous :

¹₁H + ¹₁H → ²₁H + ⁰₁^e

¹₁H + ²₁H → ³₂He

³₂He + ^x₂He → ⁴₂He + y ¹₁H

2.1) Quel nom donne-t-on à ces réactions nucléaires ?

2.2) Parmi les noyaux ³₂He , ³₁H et ⁴₂He , lesquels sont isotopes ? Justifier.

2.3) Déterminer les valeurs de x et y dans la troisième équation de réaction et justifier la réponse en précisant les lois de conservation utilisées.

2.4) On étudie dans la couronne solaire les spectres d’émission des atomes d’hélium 3 et

d’hélium 4. On rappelle qu’un spectre atomique caractérise la configuration électronique de l’atome (c’est-à-dire le nuage d’électrons de l’atome).

2.4.1) Ces deux types d’atomes possèdent-ils la même configuration électronique ? Justifier.

2.4.2) Ces deux atomes auraient-ils pu être distingués l’un de l’autre expérimentalement dans le spectre obtenu par Pierre Janssen et Norman Lockyer ?

 

 

 

©Sciences Mont Blanc

 

 

 

Sujet Bac France - Juin 2007 - III ) Synthèse d'un ester :

 

Cet exercice comporte 13 AFFIRMATIONS concernant un mode opératoire de cette synthèse.

L’aide au calcul peut comporter des résultats ne correspondant pas au calcul à effectuer.

Toute réponse doit être accompagnée de justifications ou de commentaires. A chaque affirmation, répondre par VRAI ou FAUX, en justifiant le choix à l’aide de définitions, de schémas, de calculs, d’équations de réactions,…

 

SI L’AFFIRMATION EST FAUSSE, DONNER LA RÉPONSE JUSTE.

 

Données :

Nom	Formule	Masse molaire en g.mol – 1	Masse volumique en g.mL– 1	Température d’ébullition en °C (pression 1 bar)
Acide salicylique	C7H6O3	M1 = 138		&teta;1 = 211
Méthanol	CH4O	M2 = 32	ρ2 = 0,8	&teta;2 = 65
Salicylate de méthyle	C8H8O3	M3 = 152	ρ3 = 1,17	&teta;3 = 223
Cyclohexane	C6H12	M4 = 84	ρ4 = 0,78	&teta;4 = 81

 

Formule de l’ion hydrogénocarbonate :  HCO₃^-

Masse volumique de l’eau : 1,0 g.mL^{– 1}

Couples acide/base  :   HCO₃^-(aq) / CO₃^2- (aq)

                       CO₂ , H₂O / HCO₃^-(aq); le dioxyde de carbone est un gaz peu soluble dans l’eau

 

Aide au calcul
1,38 / 2,76 = 0,500	2,76 / 1,38 = 2,00	2,1 / 7,6 = 0,28
2,1 / 3,04 = 0,69	1,52 / 2,1 = 0,72	2,1 / 1,52 = 1,4

Dans un ballon, on introduit une masse m₁ = 27,6 g d’acide salicylique, un volume V₂ d’environ 20 mL de méthanol et 1 mL d’acide sulfurique concentré.

Puis on chauffe à reflux. Sur le flacon de méthanol, on peut voir les pictogrammes suivants :

	R : 11 - Facilement inflammable. R : 23/25 - Toxique par inhalation et par ingestion. S : 7 - Conserver le récipient bien fermé. S : 16 - Conserver à l'écart de toute flamme ou source d'étincelles - Ne pas fumer. S : 24 - Eviter le contact avec la peau. S : 45 - En cas d'accident ou de malaise consulter immédiatement un médecin.

 

AFFIRMATION 1 : on doit manipuler le méthanol sous la hotte.

 

AFFIRMATION 2 : le schéma d’un chauffage à reflux est le suivant :

 

AFFIRMATION 3 : pour prélever le méthanol, il faut absolument utiliser une pipette jaugée munie d’une poire à pipeter (ou propipette).

 

AFFIRMATION 4 : la quantité n₁ d’acide salicylique introduit vaut n₁ = 2,00 x 10 ^{– 1} mol.

 

AFFIRMATION 5 : la quantité n₂ de méthanol introduit vaut environ n₂ = 5 mol.

 

AFFIRMATION 6 : l’équation associée à la réaction de synthèse du salicylate de méthyle s’écrit :

Acide salicylique

 

AFFIRMATION 7 : le réactif introduit en excès est le méthanol.

 

Après plusieurs heures de chauffage, on refroidit à température ambiante. On ajoute 100 mL d’eau glacée et on verse dans une ampoule à décanter. On extrait la phase organique avec du cyclohexane. Cette phase a une masse volumique proche de celle du cyclohexane.

AFFIRMATION 8 : la phase organique se situe dans la partie inférieure de l’ampoule à décanter.

 

La phase organique contient l’ester, du méthanol, du cyclohexane et des acides. On lave ensuite plusieurs fois cette phase avec une solution aqueuse d’hydrogénocarbonate de sodium afin d’éliminer les acides restant dans la solution. Il se produit un dégagement gazeux.

AFFIRMATION 9 : le gaz est du dioxyde de carbone.

 

On effectue à nouveau un lavage à l’eau et on sèche. On sépare les constituants de la phase organique par distillation.

AFFIRMATION 10 : lors de la distillation, le salicylate de méthyle est recueilli en premier.

 

Après purification, on récupère une masse m₃ = 21 g de salicylate de méthyle.

AFFIRMATION 11 : le rendement de cette synthèse est de 50 %.

 

AFFIRMATION 12 : l’ajout d’acide sulfurique a permis d’augmenter le rendement de la synthèse.

 

AFFIRMATION 13 : l’excès d’un des réactifs a permis d’augmenter le rendement de la synthèse.

 

©Sciences Mont Blanc

 

 

 

Sujet Bac France - Juin 2007 - I ) Synthèse d'un conservateur (spe)

 

L’acide benzoïque est un conservateur présent dans de nombreuses boissons sans alcool.

Son code européen est E 210. Il peut être préparé par synthèse en laboratoire.

Principe de cette synthèse : l'oxydation, en milieu basique et à chaud de l'alcool benzylique C₆H₅CH₂OH par les ions permanganate MnO₄^- en excès, conduit à la formation d'ions benzoate C₆H₅CO₂^– et de dioxyde de manganèse MnO₂ (solide brun). Cette transformation est totale.

Après réduction, par l'éthanol, des ions permanganate MnO₄^– excédentaires et élimination du dioxyde de manganèse MnO₂, on obtient une solution incolore contenant les ions benzoate.

L'addition d'acide chlorhydrique à cette solution permet la cristallisation de l'acide benzoïque C₆H₅CO₂H (solide blanc), que l'on recueille après filtration, lavage et séchage.

Certaines aides au calcul comportent des résultats ne correspondant pas au calcul à effectuer.

1) Questions relatives au protocole expérimental

1.1) Donner, sans justifier, le nom des parties manquantes (verrerie, nom de montage…), notées de Œ à Ž dans le texte de l’encadré ci-dessous décrivant le protocole expérimental.

1.2) Nommer sur la copie les éléments du montage de la figure 3 ci-dessus repérés par les lettres A, B et C.

1.3) Afin de caractériser le produit formé, on réalise une chromatographie sur couche mince.

Dans trois tubes à essais, on verse 1 mL d’éluant E ; dans le tube 1 on ajoute une goutte d’alcool benzylique, dans le tube 2 une pointe de spatule du solide obtenu et dans le tube 3 une pointe de spatule d’acide benzoïque pur.

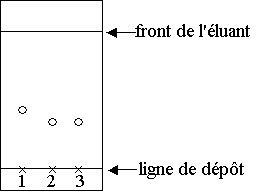On réalise une chromatographie sur couche mince à partir du contenu des trois tubes et l’éluant E puis on révèle le chromatogramme sous rayonnement UV.

Interpréter le chromatogramme réalisé lors de la synthèse et conclure quant à la nature du solide obtenu.

2) Rendement de la synthèse

Répondre, dans cette seconde partie, en choisissant la bonne réponse. Justifier clairement ce choix (définition, expression littérale et application numérique, tableau d’avancement …).

Une réponse non justifiée ne sera pas prise en compte.

 

Données :

2.1) L’oxydation se fait en milieu basique. L’équation chimique de la réaction d’oxydoréduction qui se produit entre l’alcool benzylique et les ions permanganate s’écrit :

3 C₆H₅CH₂OH (l) + 4 MnO₄^- (aq) = 3 C₆H₅CO₂^-(aq) + 4 H₂O (l) + 4 MnO₂ (s) + HO^- (aq)

 

Les couples oxydant / réducteur mis en jeu lors de la synthèse de l’acide benzoïque sont les suivants :  C₆H₅CO₂^-(aq) / C₆H₅CH₂OH (l)  et  MnO₄^- (aq) / MnO₂ (s).

Choisir les deux demi-équations électroniques associées à la transformation décrite ci-dessus.

 

 

2.2) La quantité n₁ d’alcool benzylique contenue dans la prise d’essai de 2,0 mL vaut :

a) n₁ = 1,9 x 10 ^-2 mol ;

b) n₁ = 5,4 x 10 ^{- 2} mol ;

c) n₁ = 1,9 x 10 ^{- 5} mol.

Pour toute la suite, on précise que la quantité d’ions permanganate apportée vaut n₂ = 3,0.10^-2 mol.

 

2.3) Lors de l’oxydation de l’alcool benzylique, les ions permanganate doivent être introduits en excès.

Choisir la bonne proposition (on pourra s’aider d’un tableau d’évolution du système).

a) Les ions permanganate ont été introduits en excès.

b) Les ions permanganate n’ont pas été introduits en excès.

2.4). Lors de la cristallisation, le passage des ions benzoate à l’acide benzoïque se fait selon l’équation chimique :  

          C₆H₅CO₂^-(aq) + H₃O⁺  =  C₆H₅CO₂H (s)  + H₂O (l)

La masse théorique maximale m_max d’acide benzoïque qu’il aurait été possible d’obtenir vaut :

a) m_max = 1,6_.10 ^{– 2} g ;

b) m_max = 6,6 g ;

c) m_max = 2,3 g.

2.5) Le rendement r de la synthèse effectuée vaut :

a) r = 21 % ;

b) r = 61 % ;

c) r = 88 %.

©Sciences Mont Blanc