Sujet Bac Amérique du Nord Juin 2008

Calculatrice autorisée

 

Sujet complet en pdf

 

I ) Réactions totales (7 points)

II ) Détermination de la viscosité du glycérol (5 points)

III ) Le radon et ses descendants (4 points)
IV) Tuyaux sonores (spe) (4 points)

 

Sujet Bac Amérique du Nord Juin 2008 - I ) Réactions totales :

 

Les trois parties de l’exercice sont indépendantes.

1) L’ammoniac

La synthèse industrielle de l’ammoniac s’effectue en phase gazeuse. Les réactifs dihydrogène et diazote sont introduits dans les proportions stœchiométriques. La réaction a lieu en présence d’un catalyseur qui est du ruthénium sur support de graphite, sous une pression comprise entre   100.10⁵ Pa et 200.10⁵ Pa et à une température comprise entre 350°C et 500°C.

D’après : http://www.iupac.org

L’équation associée à la réaction de synthèse est :

N_{2 (g)} + 3 H_{2 (g)} = 2 NH_{3 (g)}

 

Dans un réacteur, on mélange 1,0.10² mol de diazote et 3,0.10² mol de dihydrogène.

Le taux d’avancement final de cette réaction est t = 0,70.

 

1.1) Donner l’expression du taux d’avancement final et la signification des termes utilisés.

 

1.2) La réaction de synthèse de l’ammoniac est-elle une réaction totale ? Justifier la réponse.

 

1.3) Etablir le tableau d’avancement relatif à cette réaction.

En déduire la composition finale en quantité de matière du mélange.

 

1.4) Quel intérêt a-t-on d’un point de vue microscopique à choisir une température élevée lors d’une transformation chimique ?

 

1.5) Quel est le rôle du catalyseur dans la synthèse de l’ammoniac ?

2) La solution aqueuse d’ammoniac

Données : dans les conditions expérimentales de l’exercice on a :

* Volume molaire d’un gaz : V_m = 24,0 L.mol^-1 ;

* Produit ionique de l’eau : K_e = 1,0.10 ^–14.

Un volume gazeux d’ammoniac v = 2,4.10^-1 L est dissous dans de l’eau distillée pour obtenir

V_S = 1,0 L de solution aqueuse d’ammoniac S.

 

2.1) Donner l’expression, puis calculer la quantité de matière d’ammoniac n₀ contenue dans le volume gazeux v.

 

2.2) Le pH de la solution S est mesuré et a pour valeur 10,6.

2.2.1) Rappeler la définition d’une base selon Bronsted.

2.2.2) Ecrire l’équation de la réaction modélisant la transformation chimique de l’ammoniac avec l’eau.

2.2.3) Calculer la quantité de matière en ions hydroxyde présente dans la solution S.

2.2.4) La transformation chimique associée à la réaction dont l’équation a été écrite en 2.2.2. est-elle totale ? Justifier la réponse.

 

2.3) Détermination de la constante d’acidité.

2.3.1) Donner l’expression de la constante d’équilibre associée à l’équation de la réaction 2.2.2. et déterminer sa valeur.

2.3.2) En déduire la valeur de la constante d’acidité K_a du couple : NH₄⁺/NH₃.

3) Etude d’un mélange d’acide éthanoïque et d’une solution aqueuse d’ammoniac.

Données : dans les conditions expérimentales de l’exercice on a :

* Produit ionique de l’eau : K_e = 1,0.10 ^–14 ;

* pK_a  du couple NH₄⁺ / NH₃ = 9,2 ;

* pK_a  du couple CH₃CO₂H/CH₃CO₂^– = 4,8.

 

Expérience :

Etat initial : dans un bécher on introduit V_A = 100,0 mL d’une solution d’acide éthanoïque de concentration c_A = 1,0.10^-1 mol.L^-1 et V_B = 40,0 mL d’une solution aqueuse d’ammoniac de concentration c_B = 5,0.10^-1 mol.L^-1. Dans cet état, on néglige la présence d’ions CH₃CO₂^- et NH₄⁺. Toutes les grandeurs relatives à cet état seront notées avec i en indice.

Etat d’équilibre : le pH du mélange est mesuré et a pour valeur 9,2. Toutes les grandeurs dans cet état seront notées avec eq en indice.

Questions :

La transformation chimique qui a lieu est modélisée par la réaction chimique d’équation :

CH₃CO₂H_(aq)   +  NH_3(aq)  =  CH₃CO₂^– _(aq)  + NH₄⁺_(aq)       (équation 1)

 

3.1) Détermination du quotient de réaction

3.1.1) Donner l’expression littérale puis calculer le quotient de réaction du système dans l’état d’équilibre : Q_r,eq.

3.1.2) Quelle est la valeur du quotient de réaction dans l’état initial Q_r,i ?

Le comparer à Q_r,eq et conclure sur l’évolution du système.

 

3.2) Composition du mélange

3.2.1) Pour le couple NH₄⁺/NH₃, tracer le diagramme de prédominance des espèces en fonction du pH.

3.2.2) En déduire la relation entre [NH₃]_eq et [NH₄⁺]_eq dans le mélange étudié.

 

3.3) Donner, en la justifiant, la relation entre [NH₄⁺]_eq et [CH₃CO₂^-]_eq.

 

3.4) La mesure de la conductivité de la solution S a permis de connaître la concentration en ion ammonium lorsque l’équilibre est atteint.

Sa valeur est [NH₄⁺]_eq = 7,1.10^-2 mol.L^-1.

3.4.1) En déduire la quantité de matière des espèces NH₄⁺, CH₃CO₂^- , NH₃  et CH₃COOH présentes dans le mélange à l’équilibre. On pourra s’aider éventuellement d’un tableau d’avancement.

3.4.2) La transformation chimique entre l’acide éthanoïque et l’ammoniac, modélisée par la réaction chimique d’équation 1, est-elle totale ?

 

©Sciences Mont Blanc

 

 

 

Sujet Bac Amérique du Nord Juin 2008 - II ) Détermination de la viscosité du glycérol :

 

Expérience et données:

On réalise l'expérience suivante :

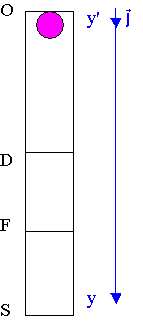
Un long tube OS, fermé aux deux extrémités, contient du glycérol de viscosité h et une bille en acier.

Le tube est retourné à l'instant t = 0, la bille se trouve alors en haut du tube sans vitesse initiale puis elle tombe verticalement dans le glycérol.

 

Données accélération de la pesanteur g = 9,81 m. s-2 Tube : hauteur : d = OS = 40 cm deux traits horizontaux, utiles dans la partie 2, ont été tracés en D et F. Bille : masse volumique de l'acier : ρs = 7850 kg.m-3 rayon de la bille : R = 6,0. 10-3 m volume de la bille V Glycérol : masse volumique : ρgly = 1260 kg.m-3 la viscosité η s'exprime en Pa.s (pascal x seconde).

 

L'étude est effectuée dans le référentiel de laboratoire supposé galiléen.

L'axe pour l'étude est l'axe y'y vertical orienté vers le bas sur le schéma ci-dessus, de vecteur unitaire .

1) Les forces

1.1) Donner l'expression vectorielle du poids de la bille  en fonction de ρ_s, V, g et .

1.2) Donner l'expression vectorielle de la poussée d'Archimède _A s'exerçant sur la bille en fonction de ρ_gly, V, g et  .

 

1.3) L'intensité de la force de frottement, donnée par la loi de Stokes, a pour expression

f = k . η . R . v ;   v est la valeur de la vitesse de chute de la bille, et k une constante sans dimension.

Donner l'expression vectorielle de la force de frottement .

 

1.4) Représenter ces forces sur un schéma sans souci d'échelle.

2) Détermination de la viscosité du glycérol, principe du viscosimètre

Au cours de la chute, la bille atteint très rapidement sa vitesse limite, notée v_lim.

Lorsque la bille passe devant le trait D et au-delà, sa vitesse est constante.

La durée de chute Δt_ch de la bille, entre les deux traits D et F qui sont distants d'une hauteur L, est mesurée.

 

2.1) Exprimer la vitesse de chute limite v_lim en fonction de Δt_ch, et L.

 

2.2) Ecrire la relation vectorielle entre les forces s'exerçant sur la bille lorsqu'elle se trouve entre les deux traits D et F. Justifier la réponse.

 

2.3) En déduire l'expression de la viscosité du glycérol  η = C . (ρ_s - ρ_gly) . (Δtch) avec :

C = g . V / (k . R . L)

 

2.4) Calculer la valeur de η, sachant que C = 7,84.10^-4 m².s^-2 et Δt_ch = 0,29 s.

 

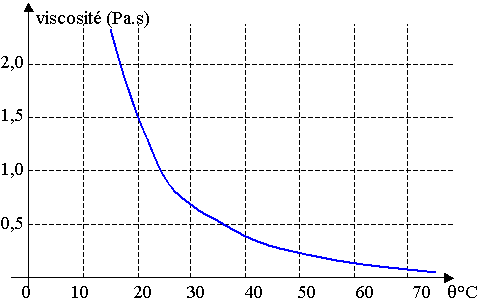
2.5) La courbe représentant la viscosité du glycérol en fonction de la température est donnée en annexe à rendre avec la copie.

Déterminer graphiquement la température à laquelle l'expérience a été réalisée.

3) Etude du mouvement de chute de la bille

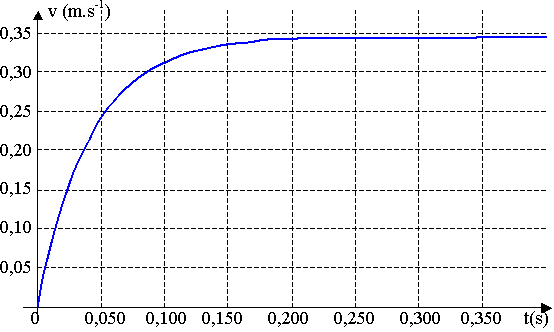
Le début de la chute a été filmé, puis le traitement de la vidéo a permis d'obtenir la représentation de la vitesse de la bille en fonction du temps.

Cette représentation est donnée en annexe à rendre avec la copie.

 

3.1) Exploitation de l'expérience.

3.1.1) Identifier graphiquement les deux phases d'évolution de la vitesse et les nommer.

3.1.2) Déterminer graphiquement :

* le temps caractéristique τ de l'évolution de la valeur de la vitesse de la bille ;

* la valeur de la vitesse limite v_lim atteinte par la bille.

3.1.3) Comment le graphe v =f(t) permet-il d'étudier l'évolution de l'accélération au cours du temps ? Décrire cette évolution.

 

3.2) Etude théorique.

3.2.1) Par application de la seconde loi de Newton, établir l'équation différentielle vérifiée par la valeur de la vitesse v de la bille.

L'écrire sous la forme :  dv/dt = A + B.v.

3.2.2) Calculer A et préciser son unité.

3.2.3) En déduire la valeur de l'accélération a₀ de la bille à l'instant t = 0.

ANNEXE à rendre avec la copie

 

2.5) Courbe représentant la viscosité du glycérol en fonction de la température

3) Etude du mouvement de chute libre

 

©Sciences Mont Blanc

 

 

 

Sujet Bac Amérique du Nord Juin 2008 - III ) Le radon et ses descendants :

 

Le radon 222 est un gaz incolore, inodore et insipide qui provient de la désintégration de l'uranium dans la croûte terrestre. Sa demi-vie radioactive de 3,82 jours est très courte mais il est régénéré en tant que membre de la filiation radioactive de l'uranium 238. L'inhalation du radon et de ses descendants représente pour la population française le tiers de l'exposition moyenne aux rayonnements ionisants. Sa présence est plus importante dans les régions granitiques et volcaniques.

La principale voie d'infiltration du radon dans une maison est le sol sur lequel le bâtiment est construit. Le radon s'accumule de préférence dans des endroits clos et peu ventilés comme les caves et, dans les maisons modernes, les vides sanitaires. Dans la plupart des cas, les moyens pour diminuer les concentrations élevées en radon sont simples : aérer et ventiler les maisons, les sous-sols et les vides sanitaires ; améliorer l'étanchéité des murs et des planchers.

Le radon 222 se désintègre en donnant successivement dans un court délai du polonium 218, du plomb 214, du bismuth 214, du polonium 214, et du plomb 210.

Tous ces descendants sont solides. Les quatre premiers peuvent être inhalés sous forme d'aérosols* et se déposer sur les cellules pulmonaires.

La nocivité du radon est surtout due aux désintégrations alpha de ses descendants.

L'énergie émise lors des désintégrations alpha est de 6,13 MeV ou 7,85 MeV

*aérosol : ensemble de particules, solides ou liquides, en suspension dans un milieu gazeux.

D'après : http://www.laradioactivite.com

 

Données :

Constante d'Avogadro : N_A = 6,02.10²³ mol^-1.

Masse molaire du radon 222 : M = 222,0 g.mol^-1.

1) Désintégration du radon 222

1.1) Donner la définition d'un noyau radioactif.

 

1.2) En s'aidant du texte, écrire les équations de désintégrations successives permettant d'obtenir les trois premiers descendants du radon 222.

 

1.3) Indiquer dans chaque cas le type de radioactivité.

2) Bilan énergétique des descendants du radon 222

2.1) L'équation de désintégration du bismuth 214 est :  ²¹⁴₈₃Bi → ²¹⁴₈₄Po +  ⁰_{- 1} e

Donner l'expression de la variation d'énergie lors de la désintégration du bismuth 214 ; préciser les unités des grandeurs dans le Système International.

 

2.2) Calculer l'énergie émise, en MeV, lors de cette désintégration.

Toutes les étapes du calcul devront apparaître.

3) Activité du radon 222

La mesure de l'activité du radon dans une cave a donné un résultat de six mille becquerels par mètre cube d'air.

Un noyau radioactif peut être caractérisé par sa constante radioactive λ. L'activité d'un échantillon radioactif à un instant t, notée A(t), est liée au nombre de noyaux radioactifs N(t) dans l'échantillon au même instant par la relation : A(t) = λ . N(t).

La demi-vie radioactive est liée à la constante radioactive λ par la relation : λ . t_1/2 = ln2.

3.1) Calculer la valeur de λ pour le radon 222.

 

3.2) Quelle est la masse de radon 222 contenue dans 1,0 m³ d'air de cette cave ?

Toutes les étapes du raisonnement devront apparaître et le résultat sera d'abord donné sous forme littérale.

 

3.3) La loi de décroissance de l'activité en fonction du temps est A(t) = A₀ . exp( - λ . t )

En supposant que le radon ne s'infiltre plus et ne s'échappe pas de cette cave, au bout de combien de jours l'activité du radon 222 sera-t-elle de 400  Bq.m^-3, seuil au dessus duquel l'Union Européenne recommande d'entreprendre des mesures correctrices simples ?

 

3.4) Quelles mesures simples faut-il prendre pour diminuer la concentration en radon dans cette cave ?

 

©Sciences Mont Blanc

 

Sujet spécialité complet en pdf

 

Sujet Bac Amérique du Nord Juin 2008 - IV ) Tuyaux sonores (spe):

 

Données :

La célérité du son dans l'air est v = 340 m.s^-1 à 15 °C.

1) Ondes sonores

1.1) Une source sonore émet en continu un son dans l’air.

Caractériser l'onde sonore qui se propage dans l'air en utilisant tout ou partie du vocabulaire suivant :

progressive, électromagnétique, transversale, mécanique, longitudinale, stationnaire.

 

1.2) Un auditeur peut déterminer la direction dans laquelle est située une source sonore S, sans la voir, quand le retard entre les vibrations reçues par ses deux oreilles D (droite) et G (gauche) est au moins égal à 1,0.10 ^{- 4} s.

L'auditeur pourra-t-il définir la direction de la source sonore S si celle-ci est située à 7,20 m de son oreille droite et à 7,10 m de son oreille gauche, la température étant de 15 °C ?

2) Tuyaux sonores à embouchure de flûte

Les tuyaux sonores à embouchure de flûte équipent en partie les tuyaux d'orgues.

Un tuyau sonore à embouchure de flûte, comprend un biseau ; l'air vient frapper ce biseau, il en découle une mise en oscillation de la colonne d'air à l'intérieur du tuyau. Ces tuyaux sont considérés comme des tuyaux ouverts au niveau de l'embouchure. L'autre extrémité du tuyau peut être :

* soit ouverte, le tuyau sonore est alors un tuyau ouvert aux deux extrémités.

* soit fermée, le tuyau est alors ouvert à une extrémité, fermé à l'autre.

 

A une extrémité ouverte, est toujours situé un ventre de vibration noté V. A une extrémité fermée, est toujours situé un nœud de vibration noté N.

 

2.1) Tuyau sonore ouvert aux deux extrémités

Un tuyau sonore de longueur L ouvert aux deux extrémités émet à q = 15 °C un son de fréquence

f = 262 Hz.

L'état vibratoire du mode fondamental du tuyau peut être représenté de la manière suivante :

 

2.1.1) A quel type d'ondes appartient le mode de vibration de la colonne d'air ?

2.1.2) Parmi les caractéristiques suivantes d'un son : intensité, hauteur, timbre, quelle est celle qui correspond à la fréquence du son ?

2.1.3) Dans le cas d'une corde tendue entre deux points fixes, donner la relation entre la distance qui sépare deux ventres ou deux nœuds successifs en fonction de la longueur d'onde.

Sachant qu'elle reste valable dans le cas du tuyau sonore, en déduire la relation entre L, v, et f.

2.1.4) Justifier l'affirmation suivante d'un élève : "A un tuyau sonore long correspond un son grave ".

2.1.5) Exprimer, en fonction de f, la longueur L₂ du tuyau qui émettrait un son dont le fondamental correspondrait à l'harmonique de rang 2 du tuyau de longueur L.

En déduire la relation entre L₂ et L.

 

2.2)Tuyau sonore fermé à une extrémité

Soit un tuyau à embouchure de flûte de longueur L₀, mais fermé à l'autre extrémité.

Ce tuyau est représenté ci-dessous dans le mode fondamental :

2.2.1) Par analogie avec une corde tendue entre deux points fixes, exprimer la fréquence f₀ du mode fondamental émis par ce tuyau en fonction de v et L₀.

2.2.2) Un élève affirme : " Un tuyau ouvert aux deux extrémités sonne avec une fréquence double de celle d'un tuyau de même longueur, fermé à une extrémité ».

Est-ce vrai ou faux ? Justifier la réponse.

2.3) Influence de ia température sur ta fréquence du son émis

Données :    La vitesse du son dans l'air est proportionnelle à T.

T est la température absolue, exprimée en Kelvin (K) ; elle est reliée à q, température exprimée en degré Celsius (°C) par la relation : T = 273,15 + q

 

Expérience : Le tuyau sonore est celui de longueur L étudié en 2.1.

On rappelle que lorsque la température q était égale à 15 °C, la célérité du son dans l'air était v et le son émis avait une fréquence f égale à 262 Hz.

On réalise une nouvelle expérience au cours de laquelle la température de l'air a augmenté de 7 °C ; la vitesse du son est devenue v' et la fréquence du son alors émis est f ’ .

 

Questions :

2.3.1) Exprimer la célérité v du son dans l'air à la température absolue T.

Exprimer la célérité v' du son dans l'air à la température absolue T’.

En déduire l'expression de v' en fonction de T, T’ et v.

2.3.2) Montrer que la nouvelle fréquence f ’ du son à la température T’ est donnée par la relation :

 f ’  = f . (T'/T)

Une oreille moyenne distingue deux sons de fréquence f et f ’ si le rapport log(f ' / f ) est supérieur à 5.10^-3.

L’oreille moyenne pourra-t-elle distinguer deux sons émis avec un écart de température de 7°C ?

 

 

©Sciences Mont Blanc