1eS - Chap 06 - Travail et puissance en mécanique

 

I ) Travail d’une force :

1)     Quand une force travaille-t-elle ?

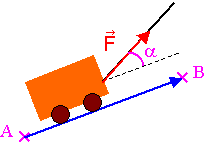Soit un chariot se déplaçant sur un trajet rectiligne AB sous l'action d'une force .

Intuitivement, on constate que les effets de la force dépendent de:

* La valeur de la force .

* L'angle α existant entre la direction de F et la direction du déplacement AB.

* La longueur AB du déplacement.

Nous allons étudier dans les paragraphes ci-dessous une grandeur physique qui caractérise les effets d'une force: le travail.

2) Travail d'une force constante

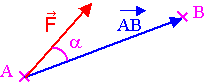Une force est constante si elle conserve la même droite d’action, le même sens et la même valeur au cours du temps.

Définition :  On appelle travail d'une force constante , lors d'un déplacement rectiligne de son point d'application de A vers B, le produit scalaire de la force F par le déplacement AB. On le note W_AB().

W_AB() = . = F . AB . cos α

W_AB() : travail en joules (J) ;  AB déplacement en mètres(m) ; α : angle entre et

Remarque: Une force ne travaille pas si :

* Son point d'application ne se déplace pas (AB = 0).

* Sa direction est perpendiculaire au déplacement (α= 90°). ⊥ .   cos( , ) = 0

Le travail d’une force ne dépend pas du chemin suivi mais du point de départ et d’arrivée.

3) Travail moteur - Travail résistant

La travail d'une force est une grandeur algébrique (positif, négatif ou nul).

Trois cas sont possibles:

* 0 < α< 90°:   cos(α) > 0 et W_AB() > 0. La force effectue un travail moteur.

* 90° < α< 180°:  cos(α) < 0 et W_AB() < 0. La force effectue un travail résistant.

* α= 90°:  cos(α) = 0 et W_AB( F ) = 0 J. La force F n'effectue aucun travail.

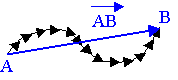4) Influence du chemin suivi :

La trajectoire AB peut être découpée en une infinité de petits vecteurs déplacements élémentaires rectilignes M_iM_i+1

W_AB() = W_AM1() + W_M1M2() + .... + W_MnB() = . + . + .... + . =  .

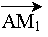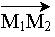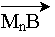Le travail d’une force ne dépend pas du chemin suivi.

II ) Travail du poids d'un corps

Soit un solide de poids  se déplaçant d'un point A d'altitude z_A vers un point B d'altitude z_B.

W_AB() =. = P . AB . cos α = m . g . AB . cos α

Dans le triangle ABC, cos α = (z_A – z_B) / AB  ;  AB . cos α = (z_A – z_B)

W_AB() = m . g . (z_A – z_B)

W_AB() travail en joules (J)  ;  m : masse en kg ;  z_A et z_B : altitudes de A et B en mètres (m)

Remarques:

* On définit aussi une différence d’altitudes h :   h = | z_A – z_B | ; on a alors  W_AB() = ± m . g . h.

* si z_A > z_B , (le mobile descend), W_AB() > 0 .  Le poids effectue un travail moteur.

* si z_A < z_B , (le mobile monte), W_AB() > 0 .  Le poids effectue un travail résistant.

V ) Puissance d'une force :

1) Exemple :

Pour soulever une charge S d'une hauteur h, une grue est plus efficace qu'un homme (la grue met moins de temps que l'homme). Pourtant, le travail effectué par la grue est le même que celui effectué par l'homme. On dit que la puissance de la grue est supérieure à celle de l'homme.

2) Définition :

La puissance mécanique d’une force caractérise sa capacité à effectuer un travail donné plus ou moins rapidement.

Soit une force qui effectue un travail W() en une durée Δt.

On appelle puissance moyenne de la force le rapport :  

P_m() = W_AB( ) / Δt

P_m() : puissance en watts (W) ; W_AB() : travail en joules (J) ; Δt : durée en secondes (s)

 

©Sciences Mont Blanc