Sujet Bac Asie Juin 2004

Calculatrice autorisée

I ) Energies d'un système solide-ressort (4 points)

I ) (spe) Lentilles et miroirs (4 points)

I ) Energies d'un système solide-ressort :

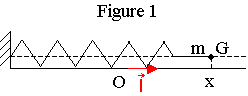
On dispose d'un système solide-ressort constitué d'un mobile de masse m = 250 g accroché à l'extrémité d'un ressort à spires non jointives, de masse négligeable et de raideur k = 10 N.m^-l.

Le mobile assimilé à son centre d'inertie G peut osciller horizontalement sur une tige parallèlement à l'axe Ox (figure 1). On étudie son mouvement dans le référentiel terrestre supposé galiléen. Le point 0 coïncide avec la position de G lorsque le ressort esl au repos.

1. Dans un premier temps, on néglige les frottements du mobile sur son rail de guidage.

1.1.1. Faire l'inventaire des forces exercées sur le mobile.

1.1.2. Reproduire la figure 1 sur la copie et représenter les différents vecteurs-forces sans souci d'échelle.

1.2. En appliquant la seconde loi de Newton au mobile, établir l'équation différentielle du mouvement.

1.3. Vérifier que x = x_M cos( (k/m) .t + φ ) est solution de cette équation différentielle quelles que soient les valeurs des constantes x_M et φ.

l.4. Le mobile est écarté de sa position d'équilibre et lâché à l'instant t = 0 s, sans vitesse initiale, de la position x₀ = + 2,0 cm,

et x_M > 0. Déterminer numériquement x_M et φ .

1.5. Calculer la période propre T₀ = 2 π (m/k) du mouvement.

2. On suppose maintenant que les frottements ne sont plus négligeables et peuvent être modélisés par une force dont la valeur est proportionnelle à celle de la vitesse et dont le sens est opposé à celui du mouvement : f = - μ.v ( μ > 0 )

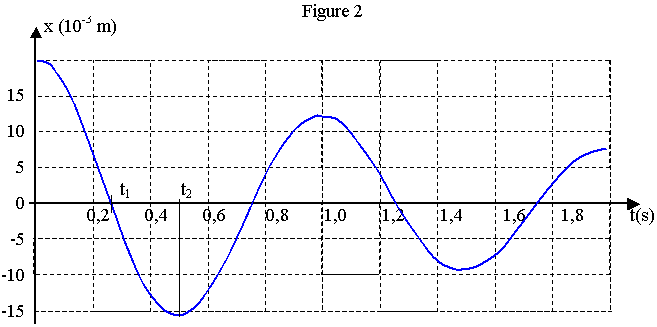
Un dispositif d'acquisition de données permet de connaître à chaque instant la position du mobile (figure 2 de la feuille annexe).

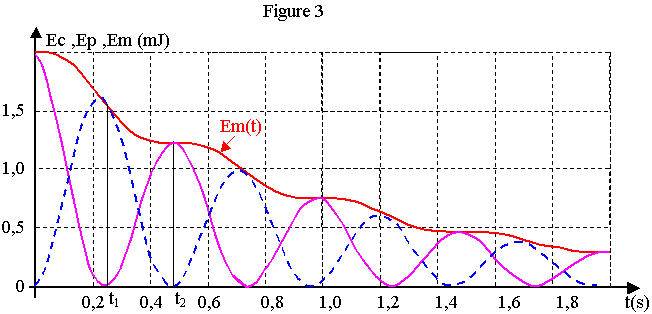
Un logiciel de traitement fournit les courbes de variation, en fonction du temps, de l'énergie mécanique (Em), de l'énergie cinétique (Ec) et de l'énergie potentielle élastique (Ep) du système solide-ressort (figure 3 de la feuille annexe).

2.1. À l'aide de la figure 2, déterminer la pseudo période T du mouvement Comparer sa valeur à celle de la période propre calculée au 1.5.

2.2. Identifier par leur lettre (A ou B) les courbes Ec(t) et Ep (t) de la figure 3 en justifiant les réponses.

2.3. Pourquoi l'énergie mécanique du système diminue-t-elle au cours du temps ?

2.4. Sur les figures 2 et 3 de la feuille annexe sont repérés deux instants particuliers t₁ et t₂ .

En utilisant la figure 2 et en justifiant la réponse, indiquer auquel de ces instants la valeur de la vitesse du mobile est :

a) maximale ?

b) nulle ?

2.5. Que peut-on en conclure quant à la valeur de la force de frottement à chacun de ces instants ? 2.6. Justifier alors la forme "en escalier" de la courbe Em (t) de la figure 3.

©Sciences Mont Blanc

II ) :

©Sciences Mont Blanc

III ) :

©Sciences Mont Blanc

I ) (spe) Lentilles et miroirs :

Cet exercice comporte 9 affirmations indépendantes concernant les lentilles convergentes et les miroirs. Toute réponse doit être accompagnée de justifications ou de commentaires.

A chaque affirmation, vous répondrez donc par VRAI ou FAUX en justifiant votre choix à l'aide de définitions, de calculs, de schémas à compléter sur l'annexe (à rendre avec la copie).

Œ Affirmation: Suivant sa position par rapport au miroir, l'image A'B' d'un objet AB donnée par un miroir plan peut être plus grande ou plus petite que l'objet.

Donnée pour les affirmations et Ž. On dispose d'une lentille convergente de 10 cm de distance focale : f ' = 10 cm.

Affirmation: Cette lentille a une vergence C = 0,10 d.

Ž Affirmation: L'image A'B' d'un objet placé devant la lentille, à 60 cm du centre optique se forme derrière la lentille, à 12 cm du centre optique.

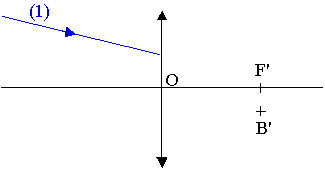
Affirmation: Après avoir traversé la lentille, le rayon (1) passe par le point B'. (voir annexe)

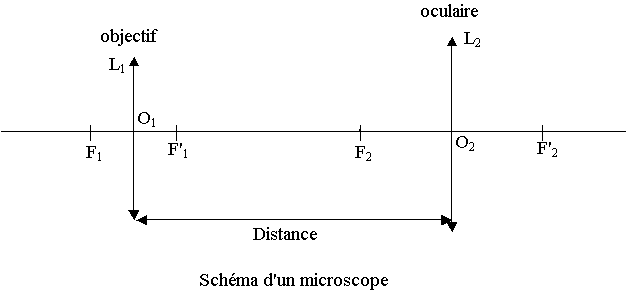
Donnée: Dans un microscope, la distance objectif-oculaire est fixe. (voir annexe)

Affirmation: Dans un microscope, le diamètre du cercle oculaire dépend de la position et de la taille de l'objet observé.

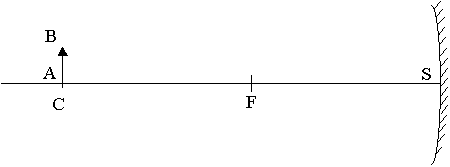
‘ Le schéma en annexe représente un miroir sphérique de sommet S, de centre C et de foyer F.

Affirmation: L'image A'B' de l'objet AB donnée par le miroir sphérique est située dans le même plan vertical que l'objet AB.

Données pour les affirmations ’,“ et ”:

* La lunette représentée en annexe est afocale: le foyer image F'₁ de l'objectif L₁ coïncide avec le foyer objet F₂ de l'oculaire L₂.

* L'objectif a une distance focale f '₁ = 0,75 m.

* Le diamètre apparent de l'astre observé est a = 9,0´10^–3 rad.

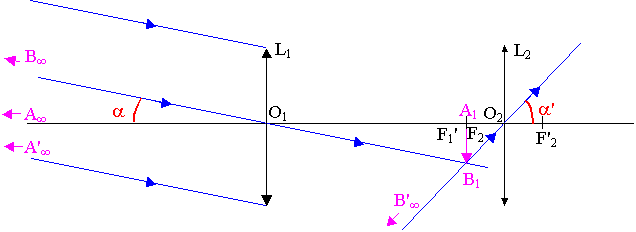
’ Affirmation: Tous les rayons issus de B qui traversent l'objectif L₁ traversent l'oculaire L₂ .(voir annexe)

“ Le grossissement d'une lunette est défini par la relation G = a' / a dans laquelle a est l'angle sous lequel on voit l'objet à l'œil nu et a ' l'angle sous lequel on voit son image dans l'instrument.

On pourra faire les approximations tan a = a et tan a ' = a ', a et a en rad.

Affirmation: Dans le cas d'une lunette afocale, le grossissement s'exprime également par la relation: G = f₁'/ f₂' f₁' étant la distance focale de l'objectif et f₂' celle de l'oculaire.

” Affirmation: L'image A₁B₁ donnée par l'objectif mesure 13,5 mm.

Annexe

Les schémas suivants peuvent éventuellement être utilisés pour répondre à certaines affirmations.

Affirmation

Affirmation ‘

Affirmation ’ et “