Sujet Bac Amérique du Nord Juin 2007

Calculatrice autorisée

 

Sujet complet en pdf

 

I ) Détermination de la teneur en élément azote d'un engrais (6,5 points)

II ) Comment déterminer le relief du fond marin avec un sondeur (5,5 points)

III ) Détermination de la concentration en dioxyde de soufre de l'air d'une grande agglomération (4 points)
IV) Etude d'un rétroprojecteur (spe) (4 points)

 

Amérique du Nord Juin 2007 - I ) Détermination de la teneur en élément azote d'un engrais :

L’ammonitrate est un engrais azoté solide, bon marché, très utilisé dans l’agriculture. Il est vendu par sac de 500 kg et contient du nitrate d’ammonium (NH₄NO_3(s)). Sur le sac, on peut lire " pourcentage en masse de l’élément azote N 34,4% ".

Afin de vérifier l’indication du fabricant, on dose les ions ammonium NH₄⁺ présents dans l’engrais à l’aide

d’une solution d’hydroxyde de sodium (Na⁺_(aq) + HO^-_(aq)).

 

Données :

Couples acide/base :                NH₄⁺_(aq) / NH_3(aq)

                                               H₂O_(l) / HO^-_(aq)

 

Produit ionique de l’eau :          K_e = 1,0×10^-14 dans les conditions de l’expérience.

 

Masse molaire en g.mol^-1 :    Azote N : 14 ;   Oxygène O : 16 ;   Hydrogène H : 1

Le nitrate d’ammonium est très soluble dans l’eau, sa dissolution dans l’eau est totale selon la réaction :       NH₄NO_3(s)  =  NH₄⁺_(aq)  +  NO₃^-_(aq)

1) Etude de la réaction de titrage

L’équation support de titrage est :          NH₄⁺_(aq)  +  HO^-_(aq)  =  NH_3(aq)  + H₂O_(l)

1.1) L’ion ammonium NH₄⁺_(aq) est-il un acide ou une base selon Brönsted ? Justifier la réponse.

 

1.2) On introduit dans un bécher un volume v = 20,0 mL d’une solution contenant des ions ammonium

à la concentration molaire apportée C = 0,15 mol.L^-1 et un volume v₁ = 10,0 mL de solution d’hydroxyde de sodium

à la concentration molaire apportée C₁ = 0,15 mol.L^-1.

Le pH de la solution est 9,2.

 

1.2.1) Compléter, sans valeur numérique, le tableau d’avancement se trouvant en annexe, à rendre avec la copie.

 

1.2.2) Calculer les quantités de matière des réactifs initialement introduites dans le bécher.

 

1.2.3) À partir de la mesure du pH, déterminer la quantité en ions hydroxyde à l’état final. Montrer que l’avancement final de la réaction x_f vaut 1,5×10^-3 mol.

 

1.2.4) Calculer la valeur de l’avancement maximal de la réaction x_max.

 

1.2.5) Que peut-on dire de la transformation ?

2) Titrage pH-métrique

Une solution d’engrais S est obtenue en dissolvant m = 6,0 g d’engrais dans une fiole jaugée de volume V = 250 mL.

On prépare ensuite les deux béchers B₁ et B₂ suivants :

 

 

Les solutions contenues dans ces béchers sont titrées par une solution d’hydroxyde de sodium (Na⁺_(aq) + HO^-_(aq))

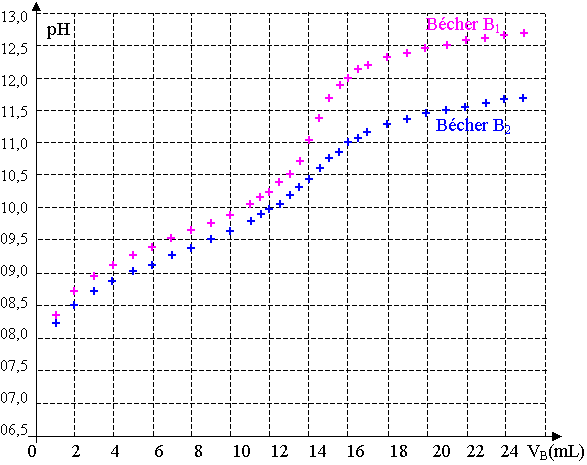
à la concentration molaire apportée C_B = 0,20 mol.L^-1. On obtient les courbes pH = f(V_B) se trouvant en annexe à rendre avec la copie.

 

2.1) Schématiser et légender le montage permettant de réaliser un titrage pH-métrique.

 

2.2) Détermination du point équivalent.

 

2.2.1) Parmi les deux courbes se trouvant en annexe, quelle est celle qui permet de déterminer les coordonnées du point d’équivalence avec le plus de précision ? Justifier le choix de la courbe.

 

2.2.2) Déterminer graphiquement les coordonnées du point équivalent sur la courbe choisie.

 

2.2.3) L’ajout d’eau déminéralisée a-t-il une influence sur le volume versé à l’équivalence ? Expliquer.

 

2.3) Quelle autre méthode, plus précise, peut-on utiliser pour déterminer le point d’équivalence ?

3) Détermination du pourcentage massique en élément azote dans l’engrais.

3.1) Définir l’équivalence d’un dosage.

 

3.2) Quelles sont les espèces chimiques présentes dans le mélange réactionnel à l’équivalence ? Justifier le pH basique de la solution en ce point.

3.3) En vous aidant, éventuellement, d’un tableau descriptif de l’évolution de la réaction, déterminer la relation entre la quantité de matière d’ions ammonium dosées n₀(NH₄⁺) et la quantité d’ions hydroxyde versés à l’équivalence n_e(HO^-).

 

3.4) En déduire la valeur de n₀(NH₄⁺).

 

3.5) Quelle quantité de matière d’ions ammonium n(NH₄⁺) a-t-on dans la fiole jaugée de 250 mL ?

En déduire la quantité de nitrate d’ammonium présente dans cette fiole.

 

3.6) Quelle masse d’azote y a-t-il dans une mole de nitrate d’ammonium ? En déduire la masse d’azote présente dans l'échantillon.

 

3.7) Le pourcentage massique en élément azote est le rapport entre la masse d’azote présente dans l’échantillon et la masse de l’échantillon.

Calculer le pourcentage massique en azote de l’échantillon. Le comparer à celui fourni par le fabricant et conclure.

 

 

Exercice I : Annexe à rendre avec la copie

 

 

Question 1.2.1

 

Équation chimique		NH4+(aq) +   HO-(aq)    =   NH3(aq)    +   H2O(l)
État du système	Avancement (mol)	Quantités de matière (mol)
État initial	0
État au cours de la transformation	x
État final si la transformation est totale	xmax
État final réel	xf

 

Question 2.3         pH = f(V_B)

 

 

©Sciences Mont Blanc

 

 

 

Amérique du Nord Juin 2007 - II ) Comment déterminer le relief du fond marin avec un sondeur :

 

Les trois parties de l’exercice sont indépendantes

1) Étude de l’onde ultrasonore dans l’eau de mer :

1.1) Définir une onde mécanique progressive.

 

1.2) L’onde ultrasonore est-elle une onde longitudinale ou transversale ? Justifier la réponse.

 

1.3) La lumière est une onde progressive périodique mais elle n’est pas mécanique.

1.3.1) Citer un fait expérimental qui permet de décrire la lumière comme une onde.

1.3.2) Quelle observation permet de montrer que la lumière n’est pas une onde mécanique ?

2) Détermination de la célérité des ondes ultrasonores dans l’eau :

La célérité des ultrasons dans l’air v_air = 340 m.s^-1 est plus faible que la célérité des ultrasons dans l’eau de mer v_eau.

Un émetteur produit simultanément des salves d’ondes ultrasonores dans un tube rempli d’eau de mer et dans l’air (voir figure 1).

A une distance d de l’émetteur d’ondes ultrasonores, sont placés deux récepteurs, l’un dans l’air et l’autre dans l’eau de mer.

Le récepteur A est relié à l’entrée A du système d’acquisition d’un ordinateur et le récepteur B à l’entrée B.

L’acquisition commence lorsqu’un signal est reçu sur

l’entrée B du système.

 

 

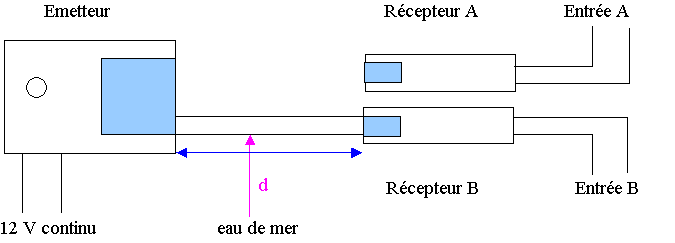
2.1) Pourquoi est-il nécessaire de déclencher l’acquisition lorsqu’un signal est reçu sur l’entrée B ?

 

2.2) Donner l’expression du retard Δt entre la réception des ultrasons par les deux récepteurs en fonction de t_A et t_B, durées que mettent les ultrasons pour parcourir respectivement la distance d dans l’air et dans l’eau de mer.

 

2.3) On détermine Δt pour différentes distances d entre l’émetteur et les récepteurs.

On traite les données avec un tableur et on obtient le graphe Δt = f(d) ci-dessous.

 

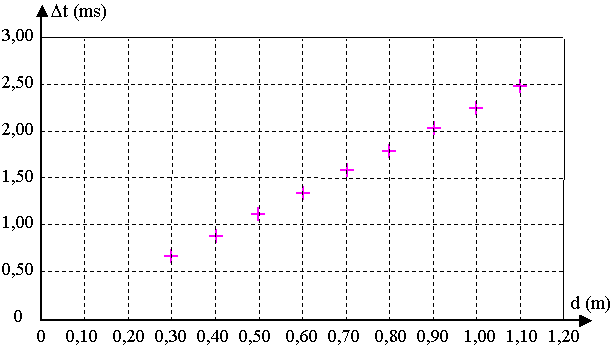
Δt = f(d)

2.3.1) Donner l’expression de Δt en fonction de d , v_air, v_eau.

2.3.2) Justifier l’allure de la courbe obtenue.

2.3.3) Déterminer graphiquement le coefficient directeur de la droite Δt = f(d).

En déduire la valeur de la célérité v_eau des ultrasons dans l’eau de mer en prenant v_air = 340 m.s^-1.

3) Détermination du relief des fonds marins :

Dans cette partie on prendra v_eau = 1,50×10³ m.s^-1.

Un sondeur acoustique classique est composé d’une sonde comportant un émetteur et un récepteur d’onde ultrasonore de fréquence f = 200 kHz et d’un boîtier de contrôle ayant un écran qui visualise le relief des fonds sous-marins.

La sonde envoie des salves d’ultrasons verticalement en direction du fond à des intervalles de temps réguliers ; cette onde ultrasonore se déplace dans l’eau à une vitesse constante v_eau.

Quand elle rencontre un obstacle, une partie de l’onde est réfléchie et renvoyée vers la source.

La détermination du retard entre l’émission et la réception du signal permet de calculer la profondeur p.

Un bateau se déplace en ligne droite suivant un axe x’x en explorant le fond depuis le point A

x_A = 0 m jusqu’au point B,  x_B = 50 m (figure 2).

Le sondeur émet des salves d’ultrasons à intervalles de temps égaux, on mesure à l’aide d’un oscilloscope la durée Δt séparant l’émission de la salve de la réception de son écho.

 

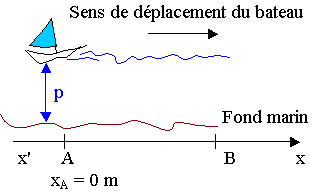
figure 2

 

3.1) L’oscillogramme ci-dessous montre l’écran d’un oscilloscope lorsque le bateau se trouve en A (x_A = 0 m). L’une des voies représente le signal émis, l’autre le signal reçu par le récepteur. Sur l’oscillogramme, on a décalé la voie 2 vers le bas pour distinguer nettement les deux signaux.

 

 

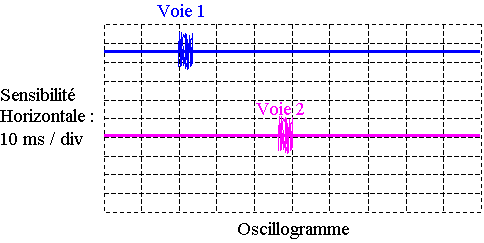
La figure 3 se trouvant sur l’annexe à rendre avec la copie représente Δt = f(x) lorsque le bateau se déplace de A vers B.

 

3.1.1) Identifier les signaux observés sur chaque voie, en justifiant.

3.1.2) A partir de l’oscillogramme, déterminer la durée Δt entre l’émission de la salve et la réception de son écho.

3.1.3) En déduire la graduation de l’axe des ordonnées de la figure 3 se trouvant sur l’annexe à rendre avec la copie représentant la durée Δt en fonction de la position x du bateau.

 

3.2) Déterminer la relation permettant de calculer la profondeur p en fonction de Δt et v_eau.

 

3.3) Tracer sur la figure 4 se trouvant sur l’annexe  à rendre avec la copie, l’allure du fond marin exploré en précisant la profondeur p en mètres en fonction de la position x du bateau.

3.4) Le sondeur envoie des salves d’ultrasons à intervalles de temps réguliers T.

Pour une bonne réception, le signal émis et son écho ne doivent pas se chevaucher.

Le sondeur est utilisable jusqu’à une profondeur de 360 m.

Déterminer la période minimale T_m des salves d’ultrasons permettant ce fonctionnement.

 

Annexe à rendre avec la copie

Question 3.1.3 et 3.3

 

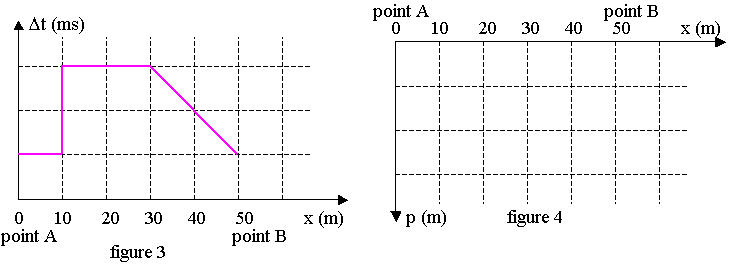
©Sciences Mont Blanc

 

 

 

Amérique du Nord Juin 2007 - III ) Détermination de la concentration en dioxyde de soufre de l'air d'une grande agglomération:

 

On se propose d’étudier dans cet exercice une des méthodes permettant de déterminer la concentration en dioxyde de soufre dans l’air :

la fluorescence ultraviolet (UV).

 

Principe de la méthode :

Dans l’air ambiant, les molécules de dioxyde de soufre SO₂ sont dans un état d’énergie « fondamental » stable E₀.

L’air ambiant est aspiré par un analyseur, filtré pour éliminer les éléments « parasites » pour la mesure, puis envoyé dans une chambre de réaction dans laquelle il est soumis à un rayonnement ultraviolet dont la longueur d’onde est λ₁ = 214 nm et provenant d’une lampe à vapeur de zinc (figure 1).

Les molécules de dioxyde de soufre de l’air sont ainsi portées dans un état d’énergie E₁.

Cet état étant instable, le dioxyde de soufre de l’air se désexcite alors très rapidement et arrive dans un état d’énergie E₂ différent de E₀ en émettant un rayonnement UV de longueur d’onde λ₂ supérieure à celle du rayonnement d’excitation.

Le rayonnement UV est reçu par un photomultiplicateur qui donne alors une tension de sortie U_S proportionnelle à la concentration en dioxyde de soufre présent dans la chambre de réaction.

 

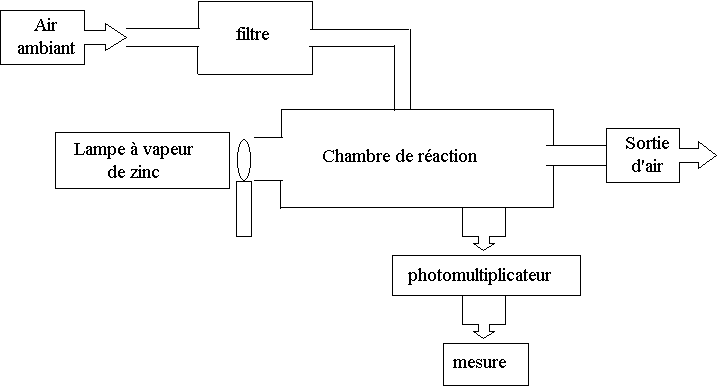
Figure 1 : schéma simplifié d’un analyseur de fluorescence ultraviolet

Données :

h = 6,63×10^-34 J.s

c = 3,00×10⁸ m.s^-1

1 eV = 1,60×10^-19 J

1 ppbv (partie par milliard en volume) = 2,66 μg.m^-3 pour le dioxyde de soufre

1) Étude du diagramme simplifié des niveaux d’énergie.

1.1) Comment appelle-t-on l’état d’énergie E₁ de la molécule de dioxyde de soufre ?

1.2) En vous aidant du texte, placer sur le diagramme en annexe, à rendre avec la copie, les états d’énergie E₀, E₁ et E₂, en justifiant la démarche.

2) Étude de la transition entre les états d’énergie E₀ et E₁.

2.1) Cette transition correspond-elle à une émission ou une absorption de lumière ?        Justifier la réponse.

2.2) Représenter sur le diagramme cette transition par une flèche notée 1.

2.3) Donner l’expression littérale de l’énergie ΔE₁ correspondant à la transition en fonction des données. La calculer en eV.

3) Étude de la transition entre les états d’énergie E₁ et E₂.

Au cours de cette transition les molécules échangent avec l’extérieur une quantité d’énergie E₂ = 3,65 eV.

3.1) Représenter sur le diagramme cette transition par une flèche notée 2.

3.2) Déterminer, en nm, la longueur d’onde de la radiation émise λ₂.

Cette radiation est-elle bien dans le domaine de l’ultraviolet ? Justifier la réponse.

4) Détermination de la concentration en dioxyde de soufre dans l’air de la grande agglomération.

4.1) L’appareil est étalonné à l’aide d’un échantillon de concentration en dioxyde de soufre de

 100 ppbv (partie par milliard en volume).

La tension à la sortie du photomultiplicateur est U₀ = 0,50 V. On effectue une mesure pour l’air d’une grande agglomération, on trouve U₁ = 0,15 V.

Déterminer la concentration [SO₂]₁ en dioxyde de soufre pour l’air de la grande agglomération en ppbv.

4.2) La limite admise pour une personne étant de 50 µg.m^-3 de gaz, l’air de la grande agglomération est-il respirable sans danger ?

 

Annexe à rendre avec la copie

Diagramme simplifié des niveaux d’énergie de la molécule de dioxyde de soufre sans considération d’échelle

 

 

 

©Sciences Mont Blanc

 

Sujet spécialité complet en pdf

 

Amérique du Nord Juin 2007 - IV ) Etude d'un rétroprojecteur (spe):

 

 

 

 

©Sciences Mont Blanc